『エターナル・フレイム』-ベクトル-レフトル-ライトル

　グレッグ・イーガンの＜直交＞三部作の第2巻『エターナル・フレイム』をよみました。

　最高だった. 科学を開拓していく物語がこんなにもおもしろい. 実験, 分析, 発見…のコンボが次々にくりだされ科学それ自体が物語になっている.

　人間離れした（※人間じゃない）頭のいい科学者が新しく発見された難しい問題を前にして難しい議論をしていく。凄まじい理解に至り超高速で新理論が打ち立てられる。見渡す限りの記念碑的偉業。記念碑の森。

　板倉先生が書かれていることの受け売りだが, ヒト世界の量子力学黎明期の奇妙な実験結果とそれを説明できる理論の発見による驚きの追体験が, カルラ・パトリジア・ロモロたちの活躍する物理学パートの軸になっている.

d.hatena.ne.jp

　その実際の歴史もある意味でこちらの宇宙の"設定"を読み解いていくという物語だった. 『エターナル・フレイム』では, 科学者たちの導きにしたがって本当にあの宇宙の設定を読ませてくれるという体験を味わわせてくれる. すごい.

　くわえて, 第一巻『クロックワーク・ロケット』から貫かれているテーマとして, 幾何学的な原理から物理法則を説明できる点がますます強調されている. あとがきにも書かれているとおり, ヒト宇宙と大きく異なる電磁場, もとい"光の場"の性質のせいで電子機器を使えない(それでロケットが「クロックワーク」なのだった). そのため観測手段が制限され, 現象の観察から大きく跳躍し"幾何学をたど"ることで基礎方程式に着地することが不可欠かつ強力な方法になるのだ. このあたりの事情は『白熱光』の"ザックの原理"などと比較できそう. スプリンターの小さな科学者たちも(物理法則の制限はないが)電子機器を持たなかったどころか光学すら未発達だった.

　一番それが色濃く出ているのが第33章. 次のような印象的な文がある.

パトリジアは呆然としたようすで、「幾何学をたどっていくとすべてがうまくおさまるんですね」
そしてカルラと視線を交わした。こういうことが起こるのをふたりが見るのは、これがはじめてではないが、幾何学をたどるという手法の持つ力は、今回はとくに圧倒的だった。

　"ベクトル":四元数が所与の数学的道具だったために, "あっけなく""レフトル・ライトル": スピノルの発見に至った過程がこの章前半で描かれている. その"あっけなさ"を示すために3人の会話が強烈なものになっているのも愛嬌.*1

　ともかく,実は<一の法則>であった<二の法則>や, 光学固体のエネルギー準位の分裂の観察から輝素波を記述するレフトル・ライトルの方程式に到達するこの過程は圧巻. 補遺2以上の基礎知識が仮定されている気もするので補間しつつ読んでみる.

　その前に著者解説ページ. 作品内で触れられたことより豊富な内容を含む. 正直到底「読んで理解した」とはいえないが以下に書いた作品の解釈が間違ってなさそうだぞという程度の確認はできた.
gregegan.customer.netspace.net.au

　なお自然単位系を使わずに

c:青色光速
h:パトリジアの定数(プランク定数)
ħ:パトリジアの定数÷(2π)

をいちいち書くことにする.

四元数

四空間における回転を記述するもっともかんたんな方法はベクトルの乗算と除算であり、
そのルールを思い出せるようカルラは表を胸に描書した。

　補遺3で説明されている通り, 早い話がこのベクトルというのはハミルトンの四元数だ. この部分以降"ベクトル"という語はおおよそ"四元数"の意味になっている. しかし, あえて"四元数"を使っていない*2のでここでもなるべく作中の議論に沿って考えてみる.

　補遺3に書かれている内容がほぼすべてだが一応基本事項をさらっておく.

　"四ベクトル"の4次元実ベクトル空間としての基底は<東>,<北>,<上>,<未来>の4つ. この記事ではEast, North, Up, Futureを略記してE,N,U,Fとする.

　ベクトルの和は単にベクトル空間の元として和をとればいい. 作中では<東>,<北>,<上>,<下>の逆元に対して<西>,<南>,<下>,<過去>の呼び名が与えられているが,使わないでおく*3.

　ベクトル空間として特殊なのはベクトルとベクトルの積がベクトルになる演算が定まっていること. カルラが"描書"したのは基底間の乗除についての表だった.

　各升目は"横×縦"を表すことに注意. 積は非可換！.

　ここでは乗算しか書かないが, 除算は積についての逆元を右からかけるだけである. 積の単位元Fに対してE,N,U,Fの逆元が-E,-N,-U,Fになることから定まる.

　慣例に従い積の記号"×"は以下省略することにして, より一般に,ベクトル v = aE+bN+cU+dF を考える. 共役なベクトル v* は v* = -(aE+bN+cU)+dF で定まる. またノルム, 長さを|v|=√(a^2+b^2+c^2+d^2)で定める. このとき成り立つのが以下の関係.

　さてここまでは「うまく体になっていてすごいな～」程度のことだが(語弊), 4次元空間の回転と結びつくことですばらしい威力を発揮する.

SO(4)

いかなる回転も、あるベクトルを左からかけ、別のベクトルで右から割ることで実現できる。
このふたつのベクトルの選択が全体の回転を決定する。

　以下の定理によって左ベクトルqL・右ベクトルqR対と4次特殊直交群SO(4)は準同型になる. つまり4次元の回転と四元数の組が対応する.

　4次元ユークリッド空間の点(x,y,z,ct)とベクトルx=xE+yN+zU+ctFを同一視する.また,ベクトルqLとqRを長さ1の単位ベクトルとする. (qL,qR)の集合は積について群になっている.
このとき,

となる一次変換A(qL,qR)が存在し,

は核を{(1,1),(-1,-1)}とする準同型写像である. A(qL,qR)は直交変換になっている.

　あまり細かく証明してもしかたないので直交変換になっていることだけ確認しておく. ベクトルvとwに対してvw*の<未来>成分Future(vw*)はユークリッド空間の標準内積になる. したがってAが直交変換であることを確かめるには内積が保たれることを見ればいい.

ちなみに単位四元数とSU(2)が同型であり, SU(2)×SU(2)がSO(4)の普遍被覆群になっている, ということらしいが連続群のことばは全然知らないのでやめとく.

　ベクトルの回転についてのこの関係により, 座標変換

に従ってベクトルの基底が変換され,

となることがいえる.

ふたつの複素平面

「複素数のペアがあるとき、その両方にマイナス一の平方根をかけたら、ふたつの数は別々に
影響を受ける。ふたつが混ざることは、いかなるかたちでも起こらず、単にそれぞれの複素平面が四分の一回転し、実数が虚数に、虚数が実数になるにすぎない。従って、もし四空間のふたつの平面をふたつの複素平面として扱うのなら、それに等価ななんらかの演算が必要になる」

　この部分では四ベクトルを2成分複素ベクトルと同一視するために, スカラー倍について検討している. 結果, √(-1)倍:各複素平面での四分の一回転は左から<上>をかけるか, 右から<上>で割る操作をすればよいことを見つけている. 後で採用しているのは結局右から<上>で割るほうなのでそれについて見てみる.

　v=aE+bN+cU+dFとしよう. 次のように2成分複素ベクトルと対応させる. 以下いちいち√(-1)と書くのはE,N,Uと混同させないため.これらはあくまで別のもの.

z=x+y√(-1)とする. vを2成分複素ベクトルとしてz倍するには,

とするとうまくいく.ただし左辺が(複素ベクトルとしての)スカラー倍で右辺がベクトル積. 確認してみよう.

　まずベクトルの積として.

　次に2成分複素ベクトルとして.

　2つの方法でスカラー倍が一致するためvを2成分複素ベクトルとみなすことが正当化される.

　スカラー倍は2つの複素平面内で独立に回転させるのみで, E-N平面とU-F平面を"混ぜない"

　しかしこれは回転と可換にならない――ベクトルをユークリッド空間のベクトルとみなす限り. つまり複素数倍を考えるためには, "ベクトルでないもの"を考える必要がある.

「つまりマイナス一の平方根をかけるのになにを使うにしろ、回転してからかけるか、
逆の順番でやるかにかかわらず、答えは同じにならないといけない」

　そこでパトリジアが思いついたのがレフトル・ライトルだった. 最高のネーミング.

「通常のベクトルが左からなにかをかけて右から割ることで回転するのに対し、この新しいもの――"左方ベクトル"(レフトル)とでも呼びましょうか――は最初の演算子か受けつけません。割り算については忘れてください」

　カルラはいった。「そんなことはない。関係は単純なものよ」
　カルラは書いた。

　　ベクトル＝レフトル÷ライトル

　「これだけ」　カルラはいった。

　ここで発見されたベクトルでないものたちは座標変換に伴って次のように変換する.

　作中では"レフトル÷ライトル"がベクトルになるとされているが, "レフトル×共役ライトル"のほうがやりやすい気がしたのでこちらを選んだ.

　ここから物理の話になっていく. 輝素波の方程式を, 4次元の幾何学に従うものするなら可能性は限られる.

　カルラは、場のレフトル、ライトルとエネルギー・運動量ベクトルの関係を、もっと伝統的な形式に変換した。そこではエネルギーと運動量は、それぞれ波の時間方向と空間方向の変化率から計算される。

　"伝統的な形式"(traditional form)ってなんやねんという感じなのだが, ヒト宇宙の物理も盗み見するとここで導かれた方程式は分かる. さらっと書いたのは簡単さであるためというよりはレフトル・ライトルほどの驚くべき発想ではないことが理由な気がするがどうか.

　まずレフトル・ライトルに働く線形作用素pを考える. 変換則が

のようにベクトルになるとすると,

によってそれぞれレフトルをライトルに,ライトルをレフトルに移す作用素であることがわかる.

　pがエネルギー・運動量ベクトルであるとすると, 輝素の運動量-周波数関係から

の置き換えができる. さらに形式的に

の置き換えができるため, エネルギー・運動量ベクトルと質量の関係から,

がここで得られる方程式ということになるだろう. この方程式は点なしスピノルと点付きスピノルの連立方程式として書いたときのディラック方程式に相当するもののよう.

　さてライトルはレフトルに縛られるため自由度は2だけになる. この自由度によって, 光学固体のエネルギー準位の分裂を説明できることが期待される.

角運動量

「新しい波動方程式でこの軸のむきが保存されるか、確認する必要があるわ。じっさいにジャイロスコープの軸のように保存するのかどうかを」

　状態の時間変化を知りたいため,次の表記を導入する.

　ただし,

積の同一の添え字については1～3に渡って和をとる.

SはSpace(空間)のSを意図している. S is for Space. ヒト世界数学でいうところのパウリ行列÷√(-1).

輝素波の方程式は

と書ける. ハミルトニアン*4を

とすると, レフトル・ライトルのペアについて

がその時間発展を決める. ただしここでは(最初から)自由な輝素波を扱っている.

　軌道角運動量との交換子*5を求める.

つまり軌道角運動量は保存しない.

　そこで「自転」;スピン角運動量Σ*6を導入しその寄与を考える.

　このΣに角運動量を名乗る資格があるのは角運動量の代数をみたすため, ということらしい.

　ハミルトニアンとの交換関係は

となる. これによって

から"軌道角運動量+自転角運動量"が保存する.

最終的な計算結果は、輝素の軌道角運動量がそれ自体では保存されないことを示していた。しかし角運動量の半分の単位を輝素自体に持たせて、その量*7は固定されるが向きは偏極の軸とともに変化できるようにすると、ふたつを組み合わせた量の変化率はゼロになり、合計の角運動量は保存された。

　ここから光の場の中で輝素がとる状態, 光学固体中のエネルギー準位のスピンによる分裂等を計算していけるはずだが, 力が足りないのでいずれこちら側宇宙のことを学んでから挑戦したい. というか解を求めないことには意味がないので早くやりたいが道が険しい.

　ロモロはカルラを見あげた。
　「これでエネルギーがスピンにどう依存するかを定量化できますね？　新しい波動方程式が、それを可能にしてくれる！」
　カルラはいった。　「それはまた明日」

参考
　はるか昔に4+0次元ディラック方程式について検討されていたらしい方のページ.
http://kuiperbelt.la.coocan.jp/sf/egan/orthogonal/dirac-orthogonal.html
　『ディアスポラ』も詳しく考察されている方. 『エターナル・フレイム』で引っかからないのはもったいないため貼っておく.

妄言
　SO(4); Special-Orthogonal-(Four)のSFなのでSFのSFだ. "S is for SO(4)"でググったりした. 絶対どっかで言われていると思う. どうでもいい.
　Greg Egan’s Home Pageから読める短編"In the Ruins"もSFのSFですね, というのは軽くネタバレ.
gregegan.customer.netspace.net.au

早川書房公式の紹介ページ
www.hayakawa-online.co.jp

*1:あまり出番がない, というかいるのかいないのか分からない記録学者のオネストだが, 控えめながらも思慮深さを感じさせる彼の姿はいいですよね. 訳者あとがきで山岸先生が触れられているように, 彼が最後に語ったことは, 理論や技術が一歩前進するための駆動力,科学者たちの思考の過程をたどることの意味とこの作品のありかたについての説明を含むのだろう. そのうえで思ったのは, 苦労は多くも発見がとんとん拍子で進んでいくようにも見えてしまうのは"編集"を受けているからためだという作者の弁明も含むのかなぁなど.……ううむ, ちょっと失礼か.

*2:ヒト世界の術語を作中で使うか否かの線引きはちょっと面白い. 人名が入るものは当然使わない.ポアソン方程式, パウリの排他律, ボソン・フェルミオン等. 　"レーザー"を頑なに使わないのは, 名称の由来がLight Amplification by Stimulated Emission of Radiationのアクロニムであまりに英語に寄りすぎているからじゃないかと思う. 　"四元数"(quaternion)を避ける理由はあまりはっきりしないが, スカラー(複素数)倍と単なる四元数の乗算を混同しないようにする目的はあるかも?

*3:というか美的感覚はともかくこれら4ついらない

*4:カルラたちが各物理量を求める方法についてはあまり明確にされていない……気がする. しかしなんにせよヒト世界量子力学と等価な方法で計算しているのはまちがいないのでここでディラックのハミルトニアンを持ち出す.

*5:そういえば交換関係とかいった言葉も作中に出てきていない. 全般的に,一度数式に翻訳することさえできればそれを解くための数学的技法は本質的ではないのでそこでいちいち躓かないというような描き方がなされている気がする.調和振動子の問題とか一瞬で解いている(ように見える)し.

*6:SはSpaceのSとか言って大文字Sを使ってしまったのが健康に悪く, ふつうここには記号Sを使うところだが逆転させた.

*7:amountの訳だが, たぶんスピン角運動量の2乗和のことなので「総和」とかのほうがそれっぽい, と思う.

〈蚊の禿〉とは

　先日ストルガツキー兄弟の『ストーカー』を読んだ。「未知との遭遇」ものの古典とのことだが、簡単にあらすじを書いておく。

～あらすじ～
　地球を訪れながら、地球人とのコンタクトを行わなずに去った「来訪者」。彼らは地球上のいくつかの地点を、異常な現象の発生する危険な土地「ゾーン」に変え、そこに人類には未知の原理に基づく謎めいた物品の数々を残していった。レドリック・シュハルトは立ち入り禁止となっているゾーンに不法侵入し、それらの収集と闇市場での売却を生業とする「ストーカー」の一人である。ゾーンからもたらされる物品による恩恵、人類に与える不気味な影響、来訪の意味――謎は謎のまま、しぶとく生きるレドリック達ストーカーを中心に、ゾーンを巡る人々の姿が描かれる。

　この作品最大の楽しみの一つは、何といっても少しでも扱いを間違えばたちまち人を死に至らしめる来訪者の遺物の数々だろう。ゾーンのひんやりとした不気味さと相まって、用途も原理も不明な物品がばらまかれている風景はとても魅力的だ。〈空罐〉、〈熱い綿毛〉、〈悪魔のキャベツ〉、〈魔女のジェリー〉、〈蚊の禿〉〈黒い飛沫〉、〈ムズムズ〉、〈適量〉……ストーカー同業者間での通称とされるこれらの名前。山括弧でくくれば何でもかっこよくなると思いおってからに～～！！！だいすき～～！！！命名の由来がきっちり分からないところもまた空想の余地があってそそられる。

　ところで原語はロシア語である。あとがきにも書かれているが原題は≪Пикник на обочине≫：「路傍のピクニック」。そのためこれら固有名詞は元はだいたい二重山括弧でくくられている。

≪Пустышка≫：〈空罐〉
≪Ведьмин студень≫：〈魔女のジェリー〉
≪Комариная плешь≫：〈蚊の禿〉
≪Зуда≫：〈ムズムズ〉

――といった具合。ロシア語版Wikipedia(Википедия)の記事のАномалии（異常現象）、Артефакты Зоны（ゾーンの人工物）の項目に一通りまとめられている。僕も全部読んだわけではないが……。
Пикник на обочине — Википедия

　さて本題に入る。気になるのは〈蚊の禿〉だ。ゾーン侵入の洗礼を与えるように浮上車〈フライング・オーバーシューズ〉に乗り込んだレドリック・研究者キリール・テンダーを待ち構える重力異常である。読んでいけば命名の由来が少しは掴めるようになるかと期待していたが、最後まで分からない。その姿と作用が比較的分かりやすく描かれるのに反して呼び名のほうははっきりしないのだ。なぜ〈蚊の禿〉？　蚊柱のようなひずみが目に見えるのかなと想像したこともあったが、読む限り完全に不可視だ。

　一方、科学者（レドリックに言わせると「石頭」）たちによる呼称は「重力凝縮場」≪гравиконцентрат≫。そのまんまだ。

　ロシア語版ウィキペディアの記事を見たのもこれが気になってのことだったのだが、素直な訳であることが分かっただけだった。Комарはずばり「蚊」。Комариныйで形容詞化され、плешь：禿にかかってまさしく「蚊の禿」。うむむ。

　いちおうこれらの語が出てくる部分をロシア語、日本語、英語で引用しておこう。特に手掛かりが得られるわけではないが。引用元は、ロシア語・英語がWikipediaの参考にも挙げられている以下のサイト。原語版に英訳が並べられている（ところでfull textを読めるのは何故）
Пикник на обочине – Roadside Picnic

　日本語は深見弾訳(1983)『ストーカー』（早川書房）。新版が2014年に復刊されているがその前に古本で買ったもの。何年本棚で眠らせていたんだ。新版は訳は特に変更されていないとのことだが未確認*1。

「重力凝縮場」

（ロシア語）
― Теперь самым малым веди ≪галошу≫ к этой гаечке и в двух метрах до неё не доходя остановись. Понял?
― Понял. Гравиконцентраты ищешь?
― Что надо, то и ищу. Подожди, я ещё одну брошу. Следи, куда упадёт, и глаз с неё больше не спускай.

（日本語訳p.41）
「それじゃ〈オーバーシューズ〉をあのボルトのところまで持っていくんだ。ただし、二歩ぐらい手前で止めろ、ぴったりくっつけるな。わかったか？」
「わかった。重力凝縮場を探しているのか？」
「おれが必要だと思うものを探しているんだ。ちょっと待った。もう一個投げる。どこへ落ちるかよく見ていろ。ボルトから絶対目を離すな。」

（英語訳）
"Now drive the boot at the lowest speed over to the nut and stop two feet away from it. Got it?"
"Got it. Are you looking for graviconcentrates?"
"I'm looking for what I should be looking for. Wait, I'll throw another one. Watch where it goes and don't take your eyes off it again."

〈蚊の禿〉

（ロシア語）
― Стой, ―говорю. ― Ни с места…
А сам взял пятую и кинул повыше и подальше. Вот она, ≪плешь комариная≫! Гаечка вверх полетела нормально, вниз тоже вроде нормально было пошла, но на полпути её словно кто-то вбок дёрнул, да так дёрнул, что она в глину ушла и с глаз исчезла.

（日本語訳p.42）
「止めろ。このまま動かすな……」
五つめのボルトを手にとると、少し高く、遠くへ投げた。そら、あれだ、〈蚊の禿〉だ！　上へ飛んでいくときは普通の飛びかただった。落ちてくるときも途中までは異常がなかったが、不意にひったくられたように脇へ外れたのだ。そのひったくられかたがあまりにも激しすぎたので、粘土の中へもぐってしまって見えなくなった。

（英語訳）
"Hold it," I said. "Don't move an inch."
I picked up another one and threw it higher and further. There it was, the mosquito mange! The nut flew up normally and seemed to be dropping normally, but halfway down it was as if something pulled it to the side, and pulled it so hard that when it landed it disappeared into the clay.

　（※太字は引用時に施した）

　英語版は訳がいくつかあるようで、新しいものでは"bug trap"の訳もあった。全文は公開されていないがサンプルページに載っている。
Roadside Picnic | Independent Publishers Group

"Bug trap"とするとその性質と結びついてなかなかしっくりくる。まさしく罠だ。しかしкомариная плешьの訳としてはかなり離れてしまっている。

　上に引用した訳では"mosquito mange"になっている。Mangeは（人以外の）獣の疥癬の意味で、「禿」そのものとは少し違う。しかし疥癬がダニの一種によって引き起こされるものであるから、それの「蚊の疥癬」とすると医学用語的な響きを持って、もしかするとそういう術語があるのかもと思わされる。

　ところでкомарを露語辞典（博友社ロシア語辞典）でひくと、成句に≪Комар носу/носа не подточит≫が口語マーク付きで挙げられている。意味は「一点非の打ちどころがない。」

　これについて検索してみると、次のような記述があった。
「ロシア語一”語”一会」
http://www.h5.dion.ne.jp/~biblio/nasu/nasu59.html

Комар носа (носу) не подточит.
意味は「文句のつけようがない」
製品を作るとき、蚊がその鋭いくちばし（нос）を突き刺せる傷がないほど表面を滑らかに仕上げたことに由来する。

　これを見ると、комариныйには、もしかするとこの成句に由来して「完璧な」の意味を持たせているのではないかという考えが浮かんでしまう。しかし辞書的にはこの形容詞に本来そういう意味はなく、検索してもそういった用例は見つからない。もっとも、ロシア語の文章を探す能力はあまりにも乏しいのだが……。

　仮にкомариныйがそういう意味だとすると、≪Комариная плешь≫は「つるっ禿」といったところだろうか。「禿」とのつながりでしっくりとくるのは確かだ。

　ではもし「つるっ禿」ならこの呼び名をつける理由は何だろう？

　作中での描写を思い出すと、「重力凝縮場」はブラックホールを思わせる。ところでブラックホールには「ブラックホール脱毛定理」なるものが知られている*2。いわく、ブラックホールの事象の地平面の外側から観測できる量は質量・電荷・角運動量に限られる。もし三つの量すべてがゼロなら「つるっ禿」になるのではないか。

　ただこの見方は問題がある。「ブラックホール脱毛定理」自体は1960年代後半から調べられていたらしいとはいえ、≪Пикник на обочине≫の発表が1972年であることを考えると、学術界の外で用いられる表現としてはやや無理があるようにも思われる。

　……と思っていたが弟ボリスБорис Натанович Стругацкийはレニングラード大学（現サンクトペテルブルク大学）で天文学を学び、1955年に卒業したあと1966年までプルコヴォ天文台で天文学者・コンピューター技師として働いていたらしい。全く「外」ではないどころかおそらく最先端に近いところにいたはずだ。
ストルガツキー兄弟 - Wikipedia
「Talkingheads-series ストルガツキー兄弟・紹介 - アトリエサード」
http://www.a-third.com/th/author/strprof.html
Братья Стругацкие — Википедия

　なお、兄アルカジイАрка́дий Ната́нович Струга́цкийは軍で日本語通訳者として働き、のちに日本文学研究者として安部公房『第四間氷期』などの翻訳を手掛けたそうだ。

　〈蚊の禿〉の意味。40年後の非ロシア語話者にそう誤解させてしまうような楽しい偶然、というところで納得しかけて他の説明を探そうとしたがかなり魅力的な説のように思われてきた。むしろ正誤はともかく遥か昔に言及されていそうだ。これに関する記述があれば教えていただけるとありがたいです。

ストーカー (ハヤカワ文庫 SF 504)

（映画もいずれ見ておきたいですね。）

追記（2016/08/19/21:33）
　@biotitさんにご指摘をいただき、≪комариная плешь≫が既に一つの成句で「つまらない」「取るに足りない」等の意味があることを知った*3。これはちょっとお粗末だった。調べるとたとえば次の同義語辞典が出てくる。
комариная плешь - это... Что такое комариная плешь?
ゾーン内のアノマリーの中でもありふれたつまらないもの、と思うとしっくりくる。

　思い返せば〈空罐〉：≪Пустышка≫は、пустой：「空の」「無意味な」に指小辞-шкаがついたもので*4、こちらにはありふれたアーティファクトであるという意味も込められていそうだ。実際に「空っぽ」であることに加えて。

　明らかな手抜かりのあることが発覚してしまい、「説得力のあるこじつけ」の感を強くしたので取り急ぎ追記した。ただ、あえてこの慣用句を選んでいる理由に〈空罐〉同様二重の意味が与えられている可能性はまだ捨てがたい。

　より広範な問題として、「SFの中に登場するブラックホール」の歴史を知る必要もありそうだ。

*1:この記事で修正すべき場所など見つかればそのときは書き直します。

*2:数学的に証明はされておらず厳密には定理ではない、ということがWikipedia英語記事などに書かれている。 No-hair theorem - Wikipedia, the free encyclopedia

*3:https://twitter.com/biotit/status/766586552327610368?lang=ja

*4:ちなみにпустышкаは辞書には「おしゃぶり」の意味で載っており、画像検索するとずらっとおしゃぶりが並ぶ。

進化の産物であること

　戦死した兵士が折り重なる戦場、骨の形が皮に浮き出た遺体の埋められた虐殺の跡、無差別テロの犠牲者が横たえられたベッドの並ぶ病院の一室……大部分が前世紀の写真である中、今世紀に入ってから撮影されたと思われるものも含まれているのに全てモノクロで統一され粗めに加工されているのは、精神的刺激を弱めるためだろうか。少なくともこういった画像に慣れない私にとっては意味のある配慮だった。遺体の画像がスクリーンに映されることは予め告げられていたため、心の備えもできていた。
　しかしこうして映し出された写真を、小さめの会議室で私が見せられている理由がまだ分からない。
「苦難の原因は何にあるのでしょう。」
彼の口から次の言葉が出てこないことからそれが実際に私に向けられた質問であることが分かった。
「悪意……ですね。人の悪意。」
期待されているであろういくつかの選択肢の中に含まれているはずの当たり障りのない答え一つを返した。話の行く先が明らかになるまで態度は変えないでいるつもりだったが、内心は混乱と胸騒ぎで落ち着きを欠きつつあった。スカウトとは彼らの信じる宗教への勧誘だったのか？これと似た問答は自宅の玄関口で経験したことがある。こういうとき話を断ち切ることができない自分の性分を後になって嘆くのだ。それとも最低限の感情移入能力とモラルの有無を見るための心理テスト？
「その通りです。」
　私の返答に一言だけで素っ気なく応じながらリモコンを操作して次のページに移ると、スクリーンに映っていたのは地震で崩壊したどこかの国の街やベッドに寝かせられた遺体――しかし今度の病室はもっと粗末で、周りの防護服に身を包んだ人々の姿から感染症の死者であることが察せられた。つまり天災や伝染病の被害の跡を撮影した写真だ。人の力では抗いがたい脅威。宗教的色合いが濃くなってゆくことに警戒しながら彼が話を再開するまでの沈黙を待った。
「人間の肉体の脆弱さや精神的な未熟さ、そういった先天的な性質が悲劇の原因です。」
　こうして説明するのはこれが初めてではないはずだ。無意識の演出なのか、スクリーンから振り返ってこちらと目を合わせ、強調するように次の言葉につなげた。
「そして苦痛は我々が進化の産物である以上必然的に備える情動です。」
　進化。その単語でここがどういった施設であったか思い出された。多少宗教がかっていても何ら不思議はない。拡張生物倫理機構――物理学者である私が招かれてやってきたこの会議室は、その国際組織の施設の一室だった。

　人工食用肉の発明と生産技術の進歩は食生活を大きく変えた。
　食肉を工場で生産することが試みられたのは近年が初めてではない。しかし家畜の筋肉をシャーレ上で組織培養できる程度の大きさではなく、食用に適するほどの大きさにまで成長させるためにはいくつもの課題を解決する必要があった。重力に耐え立体的に成長させること、栄養や酸素が細胞全てに行き届くようにすること……これらの困難は同時に、人工幹細胞によるヒト人工臓器の作成を目的とする医用工学の領域の抱える問題でもあった。そして後者には先進国の期待と需要があった。急速に発展した再生医療の分野で得られた技術のいくつかは、ほどなくして家畜の筋肉の人工的成長に転用できることが見出された。当然ヒト用の技術がそのまま使えるわけではない。だが最大の課題のいくつかは乗り越えられてしまっていた。
　食糧供給の全く新しい形態を目指す野心的な食品会社はこれに目をつけ一層研究を押し進め、ついに一般消費者向けの製品が市場に出回ることになった。最初の製品は決して安価ではなく、家畜のどの部位に対応するのかも判然としないその筋と脂肪の寄せ集めは味も食感も本物に劣り、由来の不気味さと物珍しさから新しい物好きが手に取る程度の食品でしかなかったが、価格も味も本物に遜色のない基準に至るまでにそう時間はかからなかった。清潔な工場の棚に所狭しと並ぶ、コードの繋がれた透明な箱とその中で育てられる筋肉の赤み――自然とはかけ離れたその生産現場の光景に嫌悪感をいだく者は当初は少なくなかったが、それもすぐに減った。食品会社が宣伝した通り、環境への負荷は牧場肉――「工場肉」が発明されたことによって生じた食肉のレトロニム――より遥かに低いのだ。そして家畜に苦痛を与える過程はもはや工場肉の生産ラインには存在しなかった。
　工場肉が社会に及ぼした影響は経済的な面に留まらない。今や家庭の食卓に載るようになった工場肉。脳を持つ程度に高度な生物から得られる食品を避けることは、その発明以前より遥かに容易になった。肉を食べ続けながら、食物摂取から殺生を切り離すことが可能となったのだ――菜食主義者にならずとも。ヒト以外の生命の倫理について意見することと体が肉食を求めることとの矛盾はなくなった。そして自分の関わらない問題について正しさを要求することは正義感を満たすための手頃な方法なのだ。
　とはいえ、牧場肉がただ単に食材の「自然さ」を求める美食家の嗜好品になってしまったわけではない。牧場肉と工場肉の間の溝は初期より狭まったとはいえやはり深かった。肉食の選択肢が殺生を伴うか否かの二択になってしまうほど問題は単純ではなかったが、工場肉完全移行者たちにとっては違った。
　拡張生物倫理機構の前身は、そういったヒト以外の動物の福祉を求める声の高まりと経済界との間の緩衝材として設置された組織だった。家畜のみならず、およそ生物の保護に関する事柄は全て引き受けることに名目上はなっていたが、実行力はそれほど大きなものではなかった。
　動物の権利問題は特段新しい問題ではない。前世紀から……それどころか人が肉食のあり方を自覚した時から始まっていたことだ。かかる組織が拡張生物倫理機構へと変わったのは何が理由か？それもやはり技術革新だった。

　計算機の性能は、ナノテクノロジーによって半導体の限界を超えて爆発的に向上し続けていた。あらゆる分野の研究者がそれを持て余したりはしなかった。とりわけ計算資源の余裕を渇望していたのが拡張生物倫理機構の主たる監視対象――進化的知性創発主義者だ。
　SETI――地球外知的生命探査――は依然継続されていたが、一世紀前ほどの期待が見られないのも事実だった。ところが人間は自分たちとは異なる由来を持つ知性との接触を求めるものだ。呼んでも来ないなら作ればいい。ヒト以外の知的生命と出会うための最も速い方法は、SETIではなく彼らを生み出すことだった――ソフトウェアとして。
　進化とは個体の集団がトライアルアンドエラーを絶え間なく繰り返した結果わずかずつ環境に適応してゆく遺伝的な形質の変化の蓄積だ。人工知能を開発する手段としての進化的方法は既に試みられていたし、部分的にはいくつもの成果が得られていた。しかしヒトと対等かつ模倣ではないコンタクト可能な知能となると話は違う。
　計算資源の爆発的拡大は、人工生命を進化させるためのフィールドを用意できる段階に達しつつあった。進化を推進するために必要なだけの余裕と、全くの運任せに陥らないようにするための剪定の知識が揃おうとしていた。
　宗教的熱情すら内包したこの動きは、しかし”予期せざる特異点”に目を光らせる人工知能作成に関する慎重派に警戒心を抱かせることとなった。

　「苦痛を感じられる程度に高度な神経系を持つ人工生命を生み出すことへの慎重さは何よりも優先されるべきです。自分たちにとってそれが望まないものなら。」
　彼は説明を続けた。スクリーンはいつの間にか消され、会議室に電灯がともった。
　私は道徳的義務感が全ての理由ではないことくらい知っている。子が親を凌駕すること、つまり自分たちの手に負えない知性の誕生が生み出されることへの各国の恐怖だ。知的生命の苦痛を取り除く道徳的名目を理由に、進化的方法を含むあらゆる人工知能開発が監視されている。そうでなければこの組織はこれほど大きくはならなかった。今や基準以上の計算能力を持つコンピューター全てが拡張生物倫理機構の監視下にある。その目をかいくぐる研究者はいずれ出てくるだろう。しかし現時点では高度な技術の集積である最新型計算機全てをトレースするのは難しいことではない。
　「だが既に成し遂げられたなら法の下で然るべき裁きを受けなくてはならない。」
　「進化創発主義者が成功したのですか？あなた方の監視の目を抜けて？」
　驚きは自然に質問になっていた。そのような噂は聞いたことがない。部外者である私にとっては当然だが。しかしそれを私に漏らす理由は何だ？　淡々とした彼の短い説明の行く先は未だ分からなかった。
　「そういうことではないのです。しかしそのように誤解されるのも当然でした。突拍子のないことだと思われるが聞いていただきたい。」
そう言うと彼は向かい側に腰掛けてバインダーを開き、私のプロファイルが書かれた紙を取り出した。見慣れたロゴマークが右上にプリントされている。私の所属する研究所から提供されたものだ。
　「この宇宙の物理法則が私たちにとって驚くほど優しいものであることはよく知られています。まるでそれこそが――私たちを生むことが目的であるかのように。弱い人間原理的視点では目的なるものは排するでしょう。ですが我々は目的が存在する可能性も無視できなかった。」
　話の行く先が見えてきた。当然私だってこの問題については幾度となく考えてきた。だからこそ今の研究があるのだ。
　「優しい物理法則を設定して宇宙の計算を始めること。まっさらな状態から知的生命を生み出す手段として莫大な計算能力に頼ること。人間が手を付けようとしていることそのものです。計算能力と物理法則の洗練度という点では桁が違いますが。」
　彼らは夜空に目を向けたのだ。現実世界もまたシミュレーションであるかもしれないこと。それだけなら誰だって幼い頃に考える可能性だ。しかし彼らは宇宙の慈悲深さに感謝だけを向けることはできなかった。彼らの職業がそうさせた。
　「この宇宙が誰かの計算によって始動させられたなら、その『誰か』は法の下で裁かれなければならない。そう呼びたければクリエイターと呼んでくださっても構いません。歴史的経緯から色々な意味が付加されてしまっていますが、この言葉が指す対象はそれほどぶれていないでしょう。私もそう呼ぶことにします。」
　私は確信した。彼が語っているのは少なくともいくつかの点では紛れもなく宗教だ。仮定上の存在に対する行動について語りすぎている。
　「クリエイターはもし存在するなら、進化に伴う痛みと悲嘆について無思慮すぎた。私たちが今ここにいることについての感謝はいくら捧げても不足するでしょう。しかし私たちの後ろに積み重なる進化の敗者の犠牲、勝者の獲得した暴力性、自己防衛に必要なあらゆる苦痛――そういったものの責任を帰する先でもあるのです。」
　「人間同士の争いは？最初に見せられた写真はそういうことを言いたかったのですか？つまり虐殺もクリエイターの責任になると？」
　「その言い方は単純化しすぎています。無論虐殺の罪は殺した者にあります。何も犯罪者の罪を別のところに移してしまおうと言っているわけではありません。ただ人間が同族を殺せるのは、そうした行動をとることのできる暴力性を持つ者が勝者になってきたから、という視点も誤りではないでしょう。」
　進化の起こる環境としてこの宇宙を用意した誰かを裁くこと。彼が求めるのはそういうことだろう。となると私の呼ばれた理由も見えてくる。
　「そのためにはクリエイターと意思疎通を交わすことが必要です。そして法廷まで連れてくること。あなたにはそのための研究をしていただきたい。」
　物理系の計算エラーに関する理論。おおよそ先ほど取り出された紙には私の研究についてそのようなことが書かれている。
　数学で記述された物理法則にしたがって系を進めるのは計算に他ならない。その精度は少なくとも我々の観測する限りでは無限だ。しかしもし誤りが起きるとすれば？既知の物理法則や計算機科学の理論から、その可能性について調べるのが私の研究だ。
　「私が把握している限り、現在のあなたの研究のいずれにも干渉するつもりはありません。専門分野を大きく変えてしまわない限り、私たちの目的に合致した研究をあなたは続けるでしょう。私の提案は、もし私たちの支援を受けてくださるなら、よりよい待遇と雑事から解放して差し上げることです。」
　彼らの思想を、彼らの正義を実行するために私を支援するという。とんだ酔狂だ。
　「しかし……私の研究が宇宙の計算基盤について解明できるという見込みは今のところ全くありません。私が進めているのは今のところ数学的理論を超えていない。どんな観測機器が必要になるのかも分からない。成果を上げるためには、仮説の検証のために現在進行中のあらゆる国際的科学プロジェクトより巨額の投資が必要になるかもしれない。」
　「構いません。どんな進展でも歓迎します。」
　「それどころか私の研究が計算基盤について何か観測することは全く不可能だと証明するという未来もありうる。基盤宇宙があってもそこは無人である可能性、クリエイターがいても完全にコンタクト不可能な形態の知性を持つ可能性……あなた方を落胆させる可能性はいくらでも挙げることができる。」
　「それも私たちの想定に含まれています。裁く相手がいなければそれもまた救いです。計算能力を持ちながら進化を実行させた無思慮さは発揮されていなかったことになるのですから。」
　私は混乱していた。研究に対するこんな惜しげのない支援の提案を予想してはいなかった。彼もそれを察しているのが分かった。
　「気前の良さを疑われるのは無理もないですね。ただ研究に対して支援したという実績を残すことだけを目的としているかのようなこの提案に。」
　彼が姿勢を正すのが分かった。これは彼らの支援者の思想なのか？それとも彼自身の信条なのか？
　「ですが方向付けを行うことそのものが重要なのです。クリエイターを裁くという方向付けそのもの。肉体だけに頼る時代が終わりを迎える前に、身体の脆弱さが人間を苛んできたその苦痛を自らの経験として忘れ去ってしまう前に、目標を立てねばならないのです。」
　事務的に感じさせるその口調に気圧されたのは不意打ちだった。これは彼自身の言葉だ。彼の正義がそう語らせているのだ。
　後になって知ったことだが、彼は若い頃に母親を亡くし、自身も遺伝的な要因の関係する自己免疫疾患の治療を続けていた。それが進化についての彼の考え方に影響を与えたのだろうか。決してそれが全てではないだろうが、おそらく部分的にはそうだったのだろう。

　帰り道に冬の夜空を見上げて畏怖を感じてみようとする誘惑には耐えられなかった。星々とその間に広がる真空を計算できる途方もない計算能力を持つ誰かが道徳的に人間にとって望ましい存在であるとは限らないのは確かだろう。しかしその誰かが仮に存在するとして、人間と何を共有しているとも知れないのに裁くことを目的と見据えながら研究することは健全だろうか？　少なくとも私がこの先耐えられるものであるとは今は感じられなかった。

　4世紀の後に、白色矮星シリウスBを巡るプローブ群を用いて行われたδ-アノマリーについての観測実験が〈下層宇宙〉物理学への扉を開いたとき、教義の継承者たちによって彼の言葉が意味のあるものであったと証明されたことを私は知ることになった。

～～～～～～～～～～終～～～～～～～～～～

「クリスタルの夜」*1、『神は沈黙せず』、「フェッセンデンの宇宙」を読んで。

　SFは定義からしてフィクションなので、少し自分からは距離を置いて空想を晒す手段として便利。
　突然こんなのを書いたのには理由があり、『夜と霧』を読んだことが最初のきっかけだった。ナチスの強制収容所から生還した心理学者であるフランクルによる、収容所での過酷な経験を綴った本である。紛れもない現実として人が人を虐げることが行われたことと、これを生き延び透徹した学術的な目でもってこの記録を残した作者やその仲間がいたという現実との間の隔たりに眩暈がするような気がした。
　環境が人を形成するのだから、全く同じ状況で自分ならどうなるかと考えるのも少し無理はあるが、しかし人間は高潔な精神を持つことができる一方で、先天的に悪の実行を自ら妨げる能力が備わっているわけではないということを改めて認識させられたのだった。思考能力の不備と環境の要請があれば人間は人間を殺せる。
　となると思い出されるのが『虐殺器官』だった。「虐殺の文法」とは、人が人を殺せるようにできているという脳のある意味での欠陥を突いて集団を自壊させられるプログラムなのだった。人間は進化の過程で同族を殺せるようにできてきたという事実が、いくらか誇張気味にではあるが皮肉的に描かれている。やや牽強付会であるようにも自覚するが、そう解釈すると用意された科学的下地のいくつかが腑に落ちる気がした。

　覚え書きしたいことはそれだけだったのだが、自分が進化の産物である他ならぬ現実の不気味さ（というと言い過ぎではある）から妄想を膨らませていったら創造主を裁くというような「いかにも」な話に繋がってしまった。だいたい「クリスタルの夜」のパロディー未満の何かである。『夜と霧』を読んで書くのがこれか、と不誠実さであるように感じる部分もあるが容赦してほしい。なお「クリスタルの夜」もナチスドイツ下でのユダヤ人に対する集団的な暴動と虐殺が行われた事件「水晶の夜」Kristallnachtに由来している。

　人工食用肉に関する部分は特に何も調べずに書いてかなり無責任だが前々から興味はある。将来の、自分たちが経験することになる食の形としてありうるのか？昆虫食やペースト状謎食物が皿に並ぶ未来と同程度にはありそうな気もする。

*1:グレッグ・イーガン「クリスタルの夜」"Crystal Nights"は原文がここで公開されている。 http://ttapress.com/553/crystal-nights-by-greg-egan/ 日本語訳は『プランク・ダイヴ』に収録。

クロックワーク・ロケットをとばす

グレッグ・イーガン『クロックワーク・ロケット』を考える記事（ネタバレ含む）

「山のどれくらいが太陽石だと考えているの？」ヤルダは訊いた。
「質量でたぶん三分の二」
ヤルダは背中を使ってすばやくいくつかの計算をした。
「それは四空間での四分の一回転の一回分にはじゅうぶんそうだけれど、旅の全体分をまかなえる見こみはまったくないわ」
(p.246)

　〈孤絶山〉をロケットとして打ち上げ無限の速度――母星に対して――まで加速して必要なだけの時間を得ること、それがエウセビオの計画だった。世界消失の危機に際してヤルダにこの途方もない解決策を提案する場面は1巻の折り返し点でもあり読んでいてじいんとした。できたばかりの「回転物理学」を使って種族を救う！工学者としての実現可能性にまでしっかりと言及しているからこその力強さだ。よく使われるフレーズではあるが、「ハードSFならではの感動」がここにあるだろう。

　さて、上の引用はその提案のちょっと後に続くヤルダとエウセビオの会話である。「四分の一回転」とは無限の速度まで加速することだが、〈孤絶山〉の三分の二を占めるという太陽石の量がこれに十分であることをヤルダはどのようにして出したのだろうか？回転物理学を使ってこれについて考えてみる。

　……前に一つずつの問題に際して馴染みのある私たちの宇宙でのロケットの加速について述べる。こっちのほうが簡単なので。

　注意として、以下しばらくこっちの宇宙での光速をc、ヤルダたちの宇宙の青い光の速さをbとして区別することにする。両者は本質的に同じものだが、分かりやすいようにするため。

ツィオルコフスキーの式
　ロケットの加速と質量の関係はニュートン力学の範囲では、つまり相対論を無視できる速度のときはどちらの宇宙でも次の簡単な式で表せる。

　ΔVが加速、wが推進剤の噴射速度、M0が加速前の質量、Mが加速後の質量である。
証明は質量保存と運動量保存から。
参照：ツィオルコフスキーの公式 - Wikipedia

　加速を大きくするには推進剤の噴射速度を大きくすること、加速後の質量を小さくする＝燃料積載量を大きくすることが必要になる。相対論・回転物理学でも基本は同じだが、光速に近づくにつれそれぞれその振る舞いは変わっていく。

　〈孤絶〉を回転させるための山肌へのエンジン用の穴の掘削中に、ヤルダが荒石を詰めた袋ごとカタパルトで投射されて漂流する場面があった。*1衝動的に投げ出してしまわず冷静に分析するヤルダに科学者としての賢明さを感じて惚れ惚れとするが、ここで彼女が考えたのはwをいかに大きくするか、ということだった。必要なΔVは孤絶から離れていくより大きな速度。体に蓄えられた化学エネルギーを限界まで活用するため、全力で投げられるだけの小さい石片ごとに投げることで解決しようとしたのだった。

座標変換
　特殊相対論では、S系(ct, x)に対して速度vで動く点が静止しているように観測されるS'系(ct', x')への座標変換は、座標原点を一致させてかつ空間回転は無いものとすると次のように行列を使って表される。

　一方、回転物理ではS系(bt, x)からS'系(bt', x')への変換は

のようになる。ローレンツ変換に対してウィック回転の考え方を使ってtをitに、vをivに置き換えると簡単に得られるが、素朴に計量が形を変えないこと（つまり直交行列になること）と変換の相対性から導くこともできるだろう。ややごちゃごちゃした見た目だが、座標軸の原点を中心にした回転をパラメータvで表しただけ。vに平行なxの成分をx∥、垂直な成分をx⊥とすると、

と分かりやすく表せる。

4次元空間での座標変換を表してみたが、専ら直線的な運動を扱うためよく見る2×2行列による変換で充分だろう

私たちの宇宙

ヤルダたちの宇宙

ここから相対論的な（あるいは回転物理の）速度の合成則が出せる。
S'系で速度wの点がΔt'の間にΔx'=wΔt'動くとすると、上の逆変換から、S系での座標差と速度は

同様にしてヤルダたちの宇宙での速度の合成則は

これらを使って相対論的なロケットの加速を考える。

相対論的なロケット
　母星を発ったロケットが速度Vで動いている瞬間を考える。これが静止して見える系S、すなわちロケットとともに速度Vで運動する系で見る。「四空間」（4次元時空）上ではこれはロケットの「来歴」（世界線）に接する直線を時間軸、それと直交する3次元部分空間が空間となる系として捉えることができる。

　この瞬間を母星系で時刻t、次の加速後を時刻t+dtとする。この間にロケットが静止質量dμの推進剤*2を後方に速度wで噴射したとすると、4次元的な運動量の保存則から次の式が得られる。

せっかくcとbで区別していたがまとめて扱ってしまうためcで統一した。複号は上の-が相対論、下の+が回転物理。
微小量dvは加速後のロケットのS系での速度である。微小量の1次の項だけ残すと、等式は

と書き換えられ、さらにdμを消去すると

を得る。速度の合成則から、t+dtでの速度は母星系で

dvを消去した後変数分離して積分すると、

t=0で速度0、質量M0として積分定数を決めた。見てのとおり符号の違いがtanhとtanの違いをもたらしている。図示するとこの通り。原点近傍で3つがほぼ一致していることも分かる。

推進剤の噴射速度を大きくするほど、加速後のMを小さく（燃料の質量比を高く）するほど最終的に得られる速度が大きくなるのはどの場合も同じだが、相対論では光速cが壁になっていることが分かる。一方回転物理では有限の燃料で無限の速度に達することができる。
その量は質量比で

これが往路での加速に必要な太陽石の質量比の下限ということになるだろう。
仮にエウセビオの言った通り2/3だとすると、

と熱したガスは紫外線（青い光の約1.5倍程度の領域）程度の噴射速度が必要になる。

――という結果を得たがガスをそんなに高速で噴射できるだろうか……。
それよりありそうな可能性は光の運動量の寄与が無視できないほど大きいということのような気がする。*3

　ではもし速度無限の推進剤を、すなわち「紫外極限」の光だけを放出することができるとしたら？数学的な極限操作に対して大らかになればそれは燃料を消費することなく推進できることを意味する。それこそが〈永遠の炎〉であり、この実質的な第二種永久機関を見つけ出せるか否かに〈孤絶〉が故郷に帰れるか否かが賭けられているのだった。

燃焼効率
　私たちの宇宙でもっとも効率がいい推進剤は質量を全てエネルギーに変えてしまえるもので、それは通常物質と反物質との反応になる。質量Mのロケットがそのうちdmの推進剤を後方へ速度wで噴射して速度dVを獲得するとする。そのうちさらに割合εがエネルギーに変わる（質量欠損）とき、4元運動量の保存から、

時間成分にのみ注目すると、

　これが推進剤の噴射速度wと変換効率εの関係になる。化学燃料や核分裂・核融合を使う限りεは極めて小さいが、もしε=1を実現できればw=cとなり、質量を全てエネルギーに転換できる。物質と反物質の対消滅によるγ線の放出によってこれが実現される。

　ではヤルダたちの宇宙ではどうか。今度は質量欠損ではなく「質量獲得」が起こる。
さっきと同じような状況で、しかし推進剤が割合εの質量を得るとして計算する。

　乱暴な計算だがここでwdmを一定値dpに保ちながらwを無限大とする。すると

　と、ロケットからの質量の損失dmがゼロでありながら加速することができる。これがエネルギーの保存則に反することなく、光を放つだけで加速させることのできる〈永遠の炎〉だ。

　同じようなことは私たちの宇宙ではできない。もっとも効率が良くてεを1にすること、つまり物質-反物質対消滅による推進が限界になり、燃料無しに自力で加速することはできない。〈永遠の炎〉はある意味で反物質による推進に例えることもできそうだが（「ネレオの矢」の話などいかにもそれらしい）、決定的な違いがここにある。

光子
　計算していて気になったことだが、ヤルダたちの宇宙では光子が静止質量を持つとみなせるらしい。（そもそも「光子」に対応するものが存在すると考えてもいいのか分からないが、四空間上の波数ベクトルに平行なエネルギー運動量という概念をヤルダたちはかなり自然なものとしてみなしているように感じる。）私たちの宇宙と違ってノルムが0のベクトルは0ベクトル意外に存在しない――正定値計量として当然の性質――ため、運動量を持つなら必ず大きさも持つことになるためだ。定量的な解釈は量子論以前にとりあえず古典的な光の場の理論（≒電磁気学）を待たねばならないが、私たちの宇宙との面白い違いだ。

第三宇宙速度
　今までとほとんど関係ない話だが、エウセビオが小型ロケットの試験打ち上げを行う場面でさらっと第三宇宙速度が第二宇宙速度の3倍であることに言及される（p.273）。ちなみに私たちの地球と太陽ではその比は1.5倍程度。だが「ハビタブルゾーン」の概念も違う（そもそも液体が存在しない）ためここから言えることはほとんどなさそう。

気になること
　話が再び回転物理でのロケットの加速に戻るが、w/cln(M0/M)をπ/2に近づけてそれを超えてしまっても普通に意味を持ち、それは負の無限大の速度から速度0へと近づいていく加速を意味する。四空間上で考えれば話は簡単で、時間軸に垂直になったのち負の傾きを持つようになるということ。しかしそのとき〈孤絶〉は母星とその周りの星の「時の矢」に対して遡ることになる。ベネデッタは往路で疾走星や直交星群の「時の矢」に逆らうことになることを心配して探査機によってそれを晴らしたが、母星の属す星群に対するそれはどう考えればよいのだろうと気になった。

まとめ
　タイトルにも含まれる「ロケット」について改めて考えてみた。〈孤絶〉の燃料の質量比を計算するための太陽石の燃焼効率の数値などを探してみたが見つからなかったので残念。しかし少なくともこっちの世界での核分裂並の激しさ、ひょっとしたら対消滅くらいに捉えてもいいのかも。『ディアスポラ』でも5+1次元マクロ球での化学反応が核融合によって進むという説明があったが、物理法則が違えばスケールも変わるものだ。この作品を読むと改めて私たちの宇宙のスケールに縛られていてはいけないことを感じさせられる。

　続きがとても気になるためOrthogonal2巻"The Eternal Flame"に挑戦し始めてみたが、英語で躓いてトホホ状態になった。ゆっくり読みながら私たちの宇宙の物理の知識も備えなければ……。

前の記事
shironetsu.hatenadiary.com

クロックワーク・ロケット (新☆ハヤカワ・SF・シリーズ)

*1:ゼロ・グラビティだ！……と言いたいところだが未見だった（知ったかぶりよくない）。一幕の事件とはいえ、アーサー・クラークや野尻抱介の短編のような味わいがある。

*2:実はこれはゼロにもなりうるので問題があるが一応その場合も含む表式が（結果的に）得られる。

*3:あるいは単に僕の計算間違いか……。

クロックワーク・ロケットをよむ

！！注意！！　グレッグ・イーガン『クロックワーク・ロケット』のネタバレを含みます。

(ヤルダの法則)

　2015年12月18日に早川書房から出版されたグレッグ・イーガンの『クロックワーク・ロケット』。

クロックワーク・ロケット (新☆ハヤカワ・SF・シリーズ)

　おもしろかった……。田舎生まれの科学者ヤルダの成長と科学者としての人生、夜空を彩る多色の星の尾、夜に咲く輝く花、不吉な「疾走星」、光についての実験から発見した「回転物理学」とそこから予想される種族に迫る滅亡の危機、それを回避すべく動き出す〈孤絶〉の計画……。科学の発見がそのまま世界の理解や事業に繋がっていくストーリーに熱くなりっぱなしだった。

　これがOrthogonal〈直交〉3部作の第1作でまだまだ続きが読める。しかしそのために電磁気学や熱力学に相当する理論が完成を見る前に終わってしまい、とてももどかしい。続き*1に進む前に作中の計算を楽しんでみることにした。

光の方程式

　表紙をめくると1ページ目から「遅い赤」という言葉で攻めてくる。光の速さは一定では――という常識を持ち込んではいけないことがここでがつんと示される。そして波長と周波数の関係こそがヤルダの理論の出発点になるのだった。それを見てみる。

　そういえば光学から入るというのは白熱光と逆の順番だと気付いた。彼らは基本的な幾何光学ですら一般相対論より随分遅れてから得たのだった。

フーリエ級数展開、フーリエ変換ではなく

「四つの次元それぞれについての波の二次の変化率を合計して、その和の符号を反転させれば、もとの波かける、定数かける、それ自体が定数である周波数の二乗の和、が得られます。そして、それが光の方程式です。」（p.152）

　光の周期-波長関係を発見し, その満たすべき微分方程式――ヘルムホルツ方程式――を予想したあとジョルジョ教授の指摘によってヤルダを悩ませたのは、方程式が指数関数的に発散する解を許容するということだった。

　これは多分斉次ヘルムホルツ方程式と呼べばいいものだと思う。Aは4元ベクトルで電磁ポテンシャルの感覚。bは補遺2のvblue=78大旅離(セヴェランス)毎停隔(ポーズ)＝青い光の速度で、空間と時間の単位を揃えるための定数。光速＝因果関係の伝搬速度の上限という意味はないし、そもそも光速は一定ですらない。

　Kは定数だが記号は勝手に置いた。〈孤絶山〉の観測所での実験によって波数と角振動数の2乗の和がこのKの2乗に等しくなることを発見してヤルダは回転物理学に到達した。『クロックワーク・ロケット』巻末の補遺2との記号の関係は、

　作中の単位を使うとおよそK=564グロス毎微離(スキャント)

　面倒なのでx0=bt,x1=x,x2=y,x3=zとしてしまう。ヤルダが収監されていたとき発見したのは円環ならうまくいくということだった。光の方程式が振動する解と同時に指数関数的発散をする解を許すという「数学的な」困難に対して時間と空間の両方が閉じていると考えるのは相当勇気のいる発想。ここにヤルダの柔軟さ（体ではなく頭の）が現れているように感じる。

このあたり『ディアスポラ』のラディヤとヤチマの多様体についての問答や、『順列都市』でマリアがオートヴァ―スから境界をなくすため3次元トーラスにしようとして断念したことなどが思い出される。

　閉じた空間の候補としてはまず球面が考えられるが、これがダメなのは境界条件を点にまで縮めてしまうことができるから。一方、円環なら、たとえばある瞬間の空間全体での光の様子などを調べないとその後の発展を知ることができない(らしい)。微分方程式の解に空間の位相幾何的な性質が反映されるという面白い話につながっているよう。

　さてヤルダの考え方をこっちの数学で表してみる。「円環」というが想像としては4次元の格子でいい。4次元ユークリッド空間を考えてt,x,y,z=xμ(μ=0,1,2,3)方向に[-Lμ/2,+Lμ/2]の周期があるとしよう。この「ブロック」、単位格子を

とおく。このときこの領域で定められた関数f,gに対して内積と正規直交基底を以下のように定められる。

が正規直交基底をなすことになる。

　とりあえずヤルダの光の方程式を解いてみる。Aとφnの内積をとってみると、

が得られる。ここから、解が存在するならこれを満たす整数n0, n1, n2, n3の組が存在しなくてはならないということが分かる。格子の辺の長さLはそれぞれ決まっていて, 時空の周波数Kも決まっているから、光の方程式の解が存在すれば、ちょうどよく対応する整数が存在するようにこれらの定数もまた調整されることが必要になる。

(が実はあとでこの式が満たされていないほうが都合がいいと分かる。)

　仮にすべての辺長が同じなら

から(KL/2π)^2が自然数になることが課せられる。*2

　結局、光はこれを満たすnに応じた成分の重ね合わせということになる。

ネレオの方程式の解――ヴァレリアのポテンシャル

「あるサイズの殻にとって……外の場は完全に消失するの？」
「そのとおりよ」
ヴァレリアがヤルダの言葉を裏づけた。
「半径が最小波長の半分の倍数だと、いつでもそうなるの。そして四分の奇数波長だと、内側の場が消える。」
（p.337）

　区間は有限かつ周期境界条件が課せられるため上で述べたように本来はフーリエ級数展開で微分方程式を解くべきだが、単純化のためにはフーリエ変換でいい。これは直交関数系がほとんど連続とみなせるためで、Kと宇宙の径の大きさがその理由になっている。

「このすべては単なる理想化だが――宇宙をなめらかに包む必要から、制約の追加とそれによる複雑化が余儀なくされる――それは出発点だ。」（p.288）

　ここは多分本来はフーリエ級数展開を使うべきであるといういうことを言っている。

　そういうわけで空間を無限とみなしてネレオの方程式の解、特にヴァレリアが求めた球殻状の光源の周りの場を計算してみる。

ヘルムホルツ方程式のグリーン関数

　関係ないがグリーン関数やグリーンの恒等式に名を残すジョージ・グリーンはパン屋さんだったらしい。ヤルダがパンのための小麦を育てていたことをちょっと思い出す。

　解くべきものは3,4次元のヘルムホルツ方程式だが、一般にn次元のヘルムホルツ方程式のグリーン関数Gを求めてみる。回転に対して不変であるという条件を課し、動径rにのみ依存するとすると、極座標への変換から以下のような式が得られる。*3

ここでνを用いて以下のような置き換えをする。

ν=(n-2)/2としてr~=Krと置くことで解くべき式は次のような形になる。

r≠0で左辺は0となるためこれはν次の(r~についての)ベッセルの微分方程式になる。
この微分方程式の解には線形独立なものが2つ存在して、ν次のベッセル関数Jν, ノイマン関数Yνの線形和として表せることが知られている。

（Wikipedia英語版の記事。日本語版もあるが公式が少ない。https://en.wikipedia.org/wiki/Bessel_function　）

係数a,bを決めるために再び微分方程式に戻って原点を中心とした半径ε→+0の球Sで積分する。

ここでベッセル関数についての性質から、左辺第1項について、

ゆえに、

　収束性についてかなり危ない計算をした気がするが気にしない。またaの不定性が残るが、球対称性以外の境界条件を決めていないため仕方がない（と思う）。後で少し触れることだが、周期境界条件の下でフーリエ級数展開してから連続化するとこの成分が残りそう。

　さて、わざわざ一般にn次元のヘルムホルツ方程式のグリーン関数を求めたがこれから使うのはn=3だけ。n=4も時間的に変化する場に対しては必要になるはずだが多分2巻以降で使うことになるのだろう。それにしてもこっちの宇宙での波動方程式のグリーン関数の簡単さと違ってn=4は1次のノイマン関数が生で出てくるから大変そう。

　以下n=3。半整数次のベッセル・ノイマン関数は初等関数で表せる。

　これを使ってヴァレリアが求めた、球殻状に並んだ輝素の作る光の場を求めてみる。厚み無限小の、原点を中心とする半径Rの球殻状の光源の密度は$δ(R^2-r^2)$に比例する。比例係数＝面密度をσとすると、総量Qは

この光源が作る光の場 ; スカラーポテンシャルφの従うネレオの方程式は、誘電率の気持ちでε0を入れて次のようになる。

　さっき求めたグリーン関数を使ってこれを解く。極座標への変換を使った。

　これで求まった。　ようやくヴァレリアの発見の意味が分かる。最小波長λmin=2π/K(=231ピッコロ微離(スキャント)=)だから、球殻の半径が最小波長の半分の倍数のときsin(KR)のかかる外側のポテンシャルが0、4分の奇数倍のときcos(KR)のかかる内側のポテンシャルが0になる。図はp.336に載っている通り。

　ちなみにK→0としQ/ε0を-GMと読み替えることででヴィットリオの求めた質量Mの球殻の周囲の重力ポテンシャルが出る。

　また、R→0の極限では点光源の周りの場になって、

　これはネレオが光方程式に光源の項を加えたことで初めて見出した解。と思ったが本文を読むとここでQ/ε0を負に取っているらしいことに気付く。重力との類似で語っているから誘電率にあたる比例係数を負に取っているということだろう。p.288に載っている通り、距離に反比例するポテンシャルを下限として正負に振動することが分かる。これはポテンシャルなので、力としては内向きと外向きが交互に働くという奇妙な場になっている。

周期境界条件

　ここまでは境界条件を考えない単純化だった。しかし実際にはフーリエ級数展開を考えることになる…のだが、色々引っかかるのでやめた。

　静止光源の「来歴」を時間軸に対して平行として密度がδ(x)δ(y)δ(z)に比例するとすると、計算は単純。時間を無視して空間についての直交関数系で展開すればいい。*4

　動く光源の場合にもそれが静止して見えるように座標を傾けて同じ結果が得られるといいのだが、等速運動では周期性の条件から、自然数回横断して元に戻るか、宇宙の単位格子を埋め尽くすかのいずれかの場合に分かれることになる。後者の場合はめちゃくちゃ。近似解としてはさっきとそう変わらないはずだが、厳密解を求めようとすると来歴の閉じ方が分からないためやめた。

　さらに（といってもこっちは多分解決可能）、非斉次ヘルムホルツ方程式では線形作用素Δ+K^2をかけると0になる任意の関数、すなわち真空中の光を加えても式が成立する。有限区間のフーリエ級数展開では、これは光の成分の係数の発散という形で現れる。ゆえにこの宇宙で非斉次ヘルムホルツ方程式＝光源のある光の方程式が解を持つには「真空中の光」は存在してはいけないということになり、ヤルダが試みた最初の仮定に反する。

　この「真空」という表現が曲者で、全宇宙に過去にも未来にもたった1つも光源が存在しないことを意味する。ところで、こっちの宇宙では電荷0の空間でマクスウェル方程式を解くとまともな電磁波の解が得られる。この違いは光の伝搬の式が楕円形か双曲形か、という部分に起因している(らしい)。前者では1点での変化が「瞬時」に全体に及ぶのに対して、後者は1点での変化が他へ及ぶための限界の速度があり、それが物理的には光速として現れる。微分方程式の中のこの符号の違いをもたらすのが計量で、「場」の自然な方程式としてこれは避けられないのだろう。数学的にはある意味ですべてが予め決まっていなくてはならない、と言えて、まさにその点が作中時々挟まれる決定論的考えとの争いの元になっている。

　話を戻すと、多分「真空中の光」は存在しないと仮定してしまっていいのだろう。全ての光は光源に由来するべきである、という仮定でもある。ただしこの変更によって宇宙の円環構造を撤回する必要はない。

　しかしそもそも宇宙の姿として整然とした格子を想定するのが正しいのかという問題もある。この点は作中どんな理論が作られていっているのかちゃんと読めていない気もするのであまり変なことも言えないが今のところの思ったところを書いてみる。

　まず直角の格子は傾けると傾いた格子になるだけで、新しく直方体の格子を作ることはできない。宇宙は非等方的だと言える。また、ヤルダの台詞にも4次元円環以外の可能性に触れている部分があったが、もっと複雑な位相幾何的な形をしている可能性がある。さらにこの後一般相対論が見つかって平らでないことも分かっていくはず。それが光のありかたをどう変えるかは分からないけど。

　そういえば以前一般のn+1次元のマクスウェル方程式を保存則から導くというのをやったのだった。
shironetsu.hatenadiary.com
それと同じ要領で輝素の保存則とポテンシャルの方程式から光の場の幾何学を導くのもできそう。『クロックワーク・ロケット』でポテンシャルを決める方程式は出たものの、光のエネルギーと波長の関係がまだ分からなかったりするのでそのあたりを考えてみたい。というか続きを読もう。

まとめ（16/01/04追記）
　だらだらと計算式を並べるだけになってしまったが、こういう楽しみ方をできるところがこの作品のおもしろさだ。こっちの宇宙の、つまり人類の科学者達の名前が付いた定理や法則を使えないという制約があるため、どんな方程式について語っているのか一度読んだだけではいまいちピンとこないが、図もヒントになって読者も計算を確かめることができるようになっている。（ちなみに自分は白熱光を読んだときはニュートン力学を超えたところから一瞬で迷子になり、今も依然としてしっかり理解できていない。）既に固体の構造についての議論に見られる量子論の話題が入るであろう2巻以降もっと難しくなっていくようだが、こっちの宇宙の物理を学ぶモチベーションにもなりそう。

　そうして比較するとこっちの宇宙がいかに理解に優しくできているか、とくに時間の問題についてとても簡単に（というと語弊があるが）設定されているか改めて感じることもできるところがおもしろい。たとえば同時性の問題。p.392にヤルダがニノに対して〈孤絶〉と母星の同時性について説明する場面がある。〈孤絶〉の加速中、乗員にとって「同時」の母星は無限の未来にまで進み、減速するときは逆に過去に遡って見ることになる。本当に「見える」かどうかは別として、彼らの宇宙での因果律の難しさが端的に現れる。一方こっちの宇宙では加速したからと言って「同時」な時間の進み方が逆転することはない。特殊相対論は同時性の考え方を変えたが、ローレンツ計量は時間の意味をそれほど難しく変えたわけではない。

　しかしこっちの宇宙を優位であるかのように考えるべきではないのだろう。生き生きと描かれる〈直交〉宇宙たちの住人と「もう一つの物理学」は、こっちの宇宙を相対化するという試みの意味もあるように見える（と言うと少し大袈裟かも）。Diag(-1,1,1,1)や母なるこの宇宙の他の物理に万歳する前にちょっと慎重にならなくては。

*1:第2巻The Eternal FlameとThe Arrows of Timeの邦訳が2016年中に出ることが予告されている

*2:ちなみに数論にオイラーの4平方定理というものがあり、全ての自然数は必ず4つの平方数の和で表されることが平方剰余の理論から示される。 オンライン整数列辞典A014110:「nを順序付けられた4つの自然数の平方の和で表す方法の数」 https://oeis.org/A014110

*3:δ関数のこの置き換えについては太田浩一『マクスウェル理論の基礎　相対論と電磁気学』(東京大学出版会)p.26参照

*4:ちなみに波数成分を連続化してそのまま計算すると実軸上の極によって発散するが、主値積分で抑えると(こんなことしていいのか？)さっきのヴァレリアのポテンシャルと同じ結果が得られる。ついでに言うとだいたい同じ計算で3次元ヘルムホルツ方程式のグリーン関数を計算できる。

一般フィボナッチ数列の周期について(2)

(1)の続き.shironetsu.hatenadiary.com
　(1)の記事で実数列としてのフィボナッチ数列について一通り説明した.
ここからは整数列としてのフィボナッチ数列の性質を見ていく.

用語の定義

　そのまえに, 整除性の話を始めるために, ここから成分は特に述べない限り(指数や位数, 添え字を除いて)剰余環Zm=Z/mZで考えることにする. つまり前回定義した一般フィボナッチ数列はZm上の数列に, 行列ΦやGはZmに成分を持つ2×2行列の集合M(2;Zm)の元として扱うことになる. 等号はZmでの等号の意味で使うものと実数としての等号が混在することになるが, 文脈からどちらの意味か分かるようになっている(はず).

　これを踏まえ, まず「周期」や「系列」の意味をはっきりさせてしまおう.

定義2.1
　一般フィボナッチ数列{G[n]}の周期cは全てのnに対して

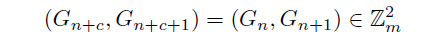
を満たす最小の自然数である.

　このように定義すれば当然その存在性が問題になるが, 鳩の巣論法と,Zm上一般フィボナッチ数列の2つ組が前後に一対一であることから明らかだろう. また, 行列でこれと同値な定義を与えるとその意味は一層明確になる.

　ΦがZm上可逆であることから結局周期とはこの最後の式を満たす最小の自然数であることが分かる. また, 同様の式を満たす自然数が全てcの倍数であり, その逆も成り立つこともほぼ明らかだろう.

　同様に出現点についても定義しておく.

定義2.2
　出現点eとは, F[e]=0 を満たす最小の自然数である.

　出現点の存在性は周期が存在することから明らかである. ただしこちらにはF[e+1]についての制約が無い.

　フィボナッチ数列では剰余について0を挟んだ両側は等しくなるから,行列を使って次のように言い換えることもできる.

出現点eとは, あるa≠0が存在して

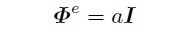
となる最小の自然数である.ただしIは単位行列.

　注意すべきことは, 周期cは初項に依存するものであるのに対して出現点は(0,1)から始まるフィボナッチ数列にのみ意味を持つことだ. 思い出しておくと, この記事で述べることはその出現点, フィボナッチ数列で最初に0が出てくる番号さえ分かれば他の系列についても大体の性質が分かるということだった.

定義2.3
(a,b)∈Zm×Zmに対して, (a,b)系列*1とは

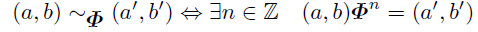
によって定まるZm×Zm上の同値関係"～Φ"による同値類である.

　一応順序をなくした同値類として「系列」の意味を定めたが, 1つ代表元を取ってΦをかければすぐに復元できる. また, この言葉を使うと周期は系列の元の個数ということになる.

　ところで0を含む系列と含まない系列があることを見たのだった. これらをそれぞれ「節有り」と「節無し」と呼び, 1周期の中に0を含む数を「節数」と呼ぼう.

定義2.4
　(0,0)系列でない(a,b)系列Cの節数sとは

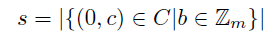
によって定まる非負整数である. このとき節有り系列は s>0 の系列であり, 節無し系列とは s=0 の系列である.

　この記事で使う言葉についての定義はこれで終わった.

p元体上の一般フィボナッチ数列

　一応一般の自然数に対して以上の用語を定めたが, ここからは専ら法は素数に限ることにする. そうするのはpに対して剰余環Zpがp元体(有限素体ともいう;記号Fpを使う)になって格段に調べやすくなるからに他ならない.

　目標としてここで証明することを先に掲げてしまおう.

以下でpは5以外の奇素数とする.

(I) p≡±1 mod 10のとき F[p-1]≡0, F[p]≡1 mod p
p≡±3 mod 10のとき F[p]≡-1, F[p+1]≡0 mod p

(II)出現点eと節有り系列の節数sについて,
e≡0 mod 4のとき s=2
e≡±1 mod4 となるのは p≡1 mod 4のときに限り, s=4
e≡2 mod 4のときs=1
なお, 節有り系列の節数は全て一致している.

(III)p≡±3 mod10,またはe≡0,1 mod 4のとき
　　　(0,0)系列を除く全ての系列の周期は(0,1)系列の周期に一致する.
　　　p≡±1 mod10かつe≡2 mod 4のとき(0,0)系列を除いて
　　　(0,1)系列の周期cより短い周期の系列が存在し, その周期はc/2

　これらを使えば前回の記事の表が, 出現点を調べるだけで書けてしまう.

　行列を使った表記については既に述べてきたが, ここからの話はp元体Fp上の2次正方行列が「主役」を演じることになる. *2

　「系列」はFp×Fp上の同値関係から定められていたが, その中の元(a,b)と次のFp上の2次正方行列Aとの全単射により, 行列間の同値関係が誘導される.

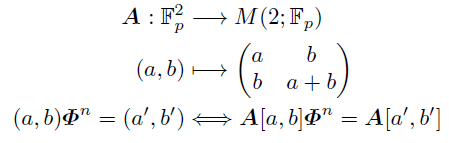
　さらにこの行列をよく見ると,

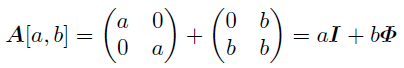
と分解できることが分かる. なお行列Aは以降もこの意味で用いることにする.

　この関係からさらに興味深い構造が見えてくるが, とりあえずは素朴な数論から
示すべきことについて述べていこう.

　まず周期と出現点,節の関係について簡単だが重要な関係を示す.

命題2.1
奇素数pに対して, (0,1)系列の周期cと出現点e,節数sについて
c=seで, s=1,2,4のいずれか.

(0,1)系列がフィボナッチ数列に対応することに注意.

証明
(0,1)系列の周期は

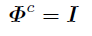
を満たす最小の自然数であり, また出現点eはあるa∈Fpが存在して

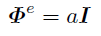
を満たす最小の自然数である.
cをeで割りc=qe+r (0≦r＜e)とすると

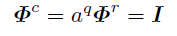
r≠0だとeの定義に反するためr=0でcはeの倍数. さらにqはa^q=1を満たす最小の自然数になる. F^e=aI, F^2e=a^2I,…,F^qe=Iよりqは節数sになるため, c=se. eとaの関係について, 行列式を比較すると,(-1)^e=a^2
(1)eが奇数のとき
　a^2=-1から a≠1, a^2=-1≠1, a^3≠1, a^4=1よりs=4.
(ii)eが偶数のとき
　a^2=1より a=1またはa=-1. よってs=1,2

(証明終)

　「F[e]=0ならF[4e+1]=1」はもっと素朴に示すこともできる.
フィボナッチ数の「加法定理」から,

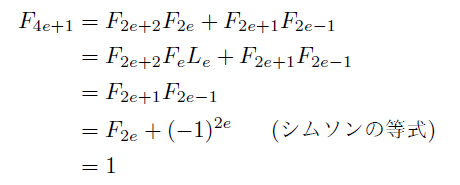
行列で計算すればすっきりするところをまわりくどくやっているだけではあるが,
フィボナッチ数列の関係式に立ち返ってみるのも悪くはない.

　上で定義した行列A[a,b]の行列式は, 系列を分類する上では本質的な意味を持つ. 同じ系列に含まれるという意味で同値な2つのFp×Fpの元は, 対応する行列式が等しいかちょうど(-1)倍になっている. (a,0)が含まれる系列では, 対応する行列式は±a^2であるから,(b,0)もまた含まれるならb^2=±a^2でなければならない. そのためこれを満たすbはaを含めて高々4個に制限されることになる.

　これで目標に掲げた(II)は部分的に示されたことになる. 先に示してしまったのは, 簡単なため.

　では目標に掲げた(I)を示そう.
カタランの公式を思い出すと, 奇素数pに対してp番目のフィボナッチ数は,

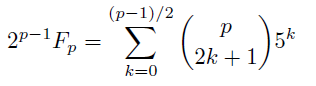
ただし今度の等号はp元体の元としての意味である. フェルマーの小定理から2^{p-1}=1, さらに2項係数について

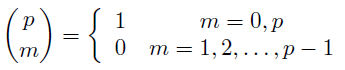
の関係を思い出すと,

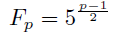
　再びフェルマーの小定理からこの値は±1であることは分かるが, そのどちらだろうか.ここで登場するのがルジャンドル記号である. つまり平方剰余が関わってくることになる.

平方剰余

　数論の基本的な内容ではあるが, 極めて重要なため平方剰余について一通り述べておこう. ここでは合同式の記号を使うことにする. またpは奇素数とする.

定義2.5
　pの倍数でないaに対して x^2≡a mod pを満たす整数xが存在するとき, aを(pに対する)平方剰余, 存在しないとき平方非剰余という.

　たとえば7に対して
1^2≡1, 2^2≡4, 3^2≡2, 4^2≡2, 5^2 ≡4, 6^2=1
から, 1,2,4は平方剰余, 3,5,6は平方非剰余である.

定義2.6
　ルジャンドル記号(a/p)は

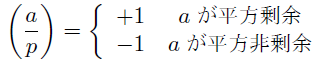
によって定められる.
法pにおいて平方剰余と平方非剰余はともに(p-1)/2個ずつ存在する.

命題2.2
　ルジャンドル記号に対して次の関係が成立する.ここでa,bはpの倍数でない整数, pとqは相異なる奇素数とする.

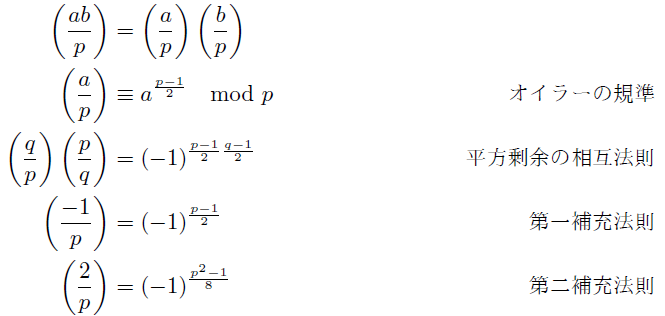
一番上の法則は
(平方剰余)×(平方剰余)=(平方剰余)
(平方非剰余)×(平方非剰余)=(平方剰余)
(平方剰余)×(平方非剰余)=(平方非剰余)
となることを言っている.

　平方剰余の相互法則はいわゆる初等数論の中でもっとも重要な定理の一つで, それを認識したガウスがそのいくつもの異なる証明を与えたことで有名である.

　平方剰余についてはとりあえずこれで十分. では中断していた証明に戻ろう
オイラーの規準からp元体Fpの元として

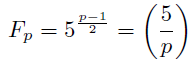
となるから, 5が平方剰余であるか否かを見ればいい. 5以外の奇素数pについて相互法則から,

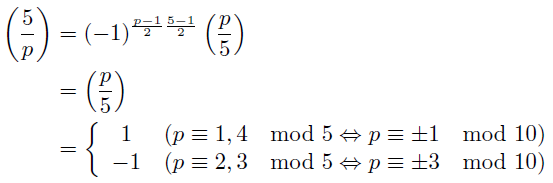
法10に置き換えられるのはpが奇数のため.

結局, 5以外の奇素数pに対して

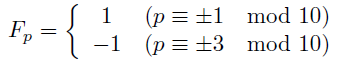
が示された.

　F[p-1],F[p+1]に対しても同じようにしてpに対する剰余を求められるが, やや煩雑である. そこで行列を使った方法を試みよう. *3

　Φに対して, ケーリー・ハミルトンの法則から,

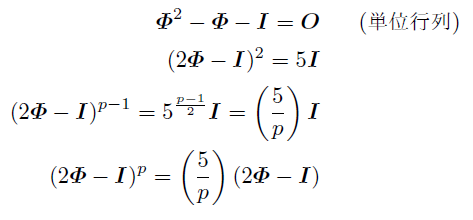
1行目から2行目で「平方完成」, 2行目から3行目で両辺(p-1)/2乗,
3行目から4行目で両辺に(2Φ-I)をかけた.
4行目の左辺を2項展開すると,

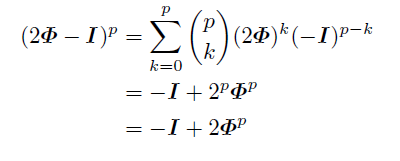
pについて場合分けすると,

(1)(5/p)=+1 ; 5が平方剰余であるとき

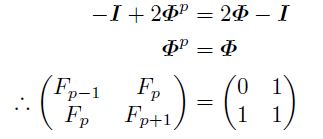
(2)(5/p)=-1; 5が平方非剰余であるとき

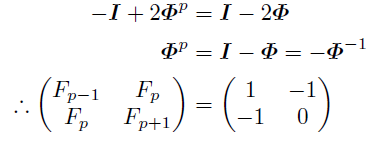
ルジャンドル記号(5/p)を使ってまとめると,

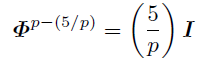
とも書ける.

　この結果は重要だ. 5が平方剰余のとき出現点も周期もp-1の約数になる.5が平方非剰余のとき出現点はp+1の約数, 周期は2p+2の(p+1以外の)約数になる.表を見ればこのことが確かめられるだろう.

　実は出現点そのものについて(この記事では)これ以上強い主張ができない. 前の記事の表を再び見ると, たとえばp=83では出現点はp+1=84, 周期は2p+2=168でたっぷりかかるパターンになっている. その一方p=89は11(p-1=88の約数)が出現点で, 周期も44と短い.表には載っていないが, 23番目のフィボナッチ数28657は素数であるため, 出現点23(28657+1を割り切って商は1246),周期92ともっと短い*4.

　この出現点と周期の性質については後で再び別証明が与えられることを見るだろう. では続いて目標に掲げた(II)(III)についてまとめて証明に入る.

対角化, ジョルダン標準形, 体の拡大

　(a,b)系列の周期cは

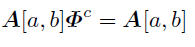
を満たす最小の自然数なのだった.

　行列で表したのだからΦを対角化しよう.固有値をλとして固有方程式を求めると,

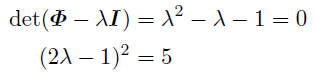
思い出さねばならないのはこれがp元体Fp上での方程式だということだ. 5が平方剰余のとき2つの異なる解が存在するが, pが平方非剰余のときFp上に解は存在せず, p=5のときは重解になる.

それぞれ場合分けして考える.

(1)5が平方剰余 ; p≡±1 mod 10のとき
　x^2=5はp元体上2つの解を持つからその一方を√5と書いてしまう. このときもう一方は-√5. そして分数を分母の逆元をかける意味で使うと結局実数の時と同じように2つの固有値は

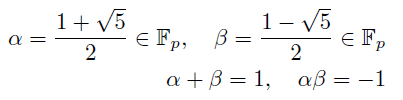
になる.2行目は解と係数の関係である.
たとえばp=19のときx^2=5の解は9,-9=10の2つで, 固有値は5,15の2つ.

　対角行列Λを次のように定めて, 各固有値に対応する固有ベクトルを並べた行列Pを用いてΦを対角化できる.

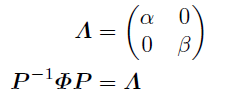
これを使ってΦのべき乗をとると周期cについて次のように書ける.

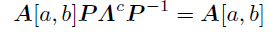
ここでA[a,b]=aI+bΦという関係があったことを思い出すと,

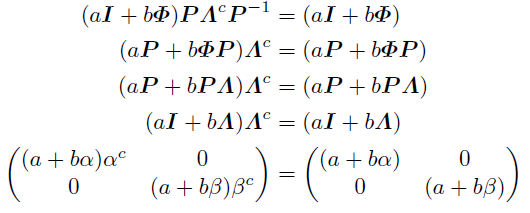
この成分を見てさらに場合分けする.

(イ)a+bα≠0かつa+bβ≠0のとき
(a+bα)(a+bβ)=a^2-ab-b^2≠0と表せて*5, cはα^c=1かつβ^c=1を満たす最小の自然数になる. ゆえにcはαとβの(Fpの乗法群での)位数の最小公約数ということになる.

(ロ)a+bα=0のとき
b=-a/α=βaで, この系列は a,βa,β^2a,β^3a… という「等比数列」になる. このときa+bβ=(2+β)a≠0(a,bがともに0とはなっていないことを仮定)だから, 周期はβの位数.

(ハ)a+bβ=0のとき
(ロ)と同様に周期はαの位数.

　αとβの位数の関係を考える. 位数の大きくないほうをα,その位数をkとする.*6

(i)kが奇数のとき

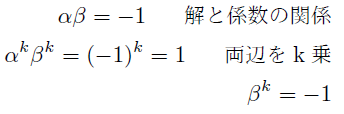
仮定よりβの位数はk以上であるため位数は2kになる. これらの公約数は2k. 結局,
a^2-ab-b^2≠0またはb=βaのとき周期2k,
b=αaのとき周期kと他のちょうど半分の長さになる.

(ii)kが偶数のとき
同様にして

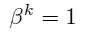
仮定からβの位数はk.
a^2-ab-b^2≠0,b=αa,b=βaいずれの場合にも周期はkになる.

　続けて出現点についても考える.出現点eはあるd≠0が存在して次の条件を満たす最小の自然数である.

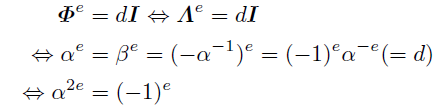
(i)eが奇数のとき
(α^e)^2=-1より-1が平方剰余になるから, 第一補充法則よりp≡1 mod 4
eはこれを満たす最小の自然数だから, αの位数はk=4e. すなわちαの位数が偶数の場合に相当し, 節数は4.

(ii)eが偶数のとき
α^2e=1となるが,α^e=-1, 1, またe≡0,2 mod 4(それぞれ自然数e'によりe=4e', e=4e'+2とおく)のときとでさらに分ける.

　　(ii-1)　α^e=-1 かつ e≡0 mod 4のとき
　　　k=2eでαの位数が偶数の場合に相当し, 節数は2.

　　(ii-2)　α^e=-1 かつ e≡2 mod 4のとき
　　
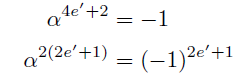
　　よりeの最小性に反す.

　　(ii-3)　α^e=1 かつ e≡0 mod 4のとき
　　
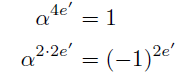
　　よりeの最小性に反す.

　　(ii-4)α^e=1 かつ e≡2 mod 4のとき
　　
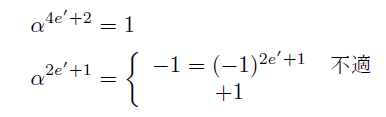
　　よってαの位数はk=2e'+1=e/2で, 奇数の場合に相当し節数は1

　まとめると
eが奇数のときk=4e, すべての系列で周期は等しく4e, 節数4
e≡0 mod4のときk=2e, すべての系列で周期は等しく2e, 節数2
e≡2 mod4のときk=e/2, (a, αa)系列で周期e/2, その他の系列は周期eで節数1

　ちなみにαとβに対してフェルマーの小定理を使うと,

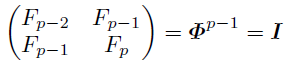
が言える.

(2)p=5のとき
　1つしかないわけだからわざわざ行列で見なくてもいいが統一的に扱う*7.
　固有方程式の解は

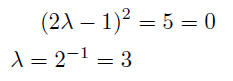
で重根を持ち対角化できないが, ジョルダン標準形には変形できる.
行列PとJが存在して, (1)と同様にして(a,b)系列の周期cを次のように表せる.

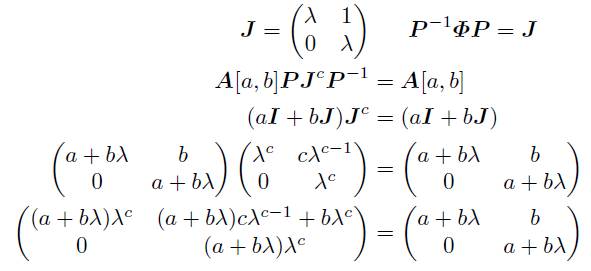
　(イ)a+bλ≠0; b≠3aのとき
　　行列の対角成分からλ^c=1. これを代入すると(1,2)成分から
　　
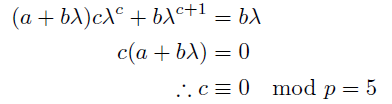
　　(「微分のような形」になって指数が肩から降りてきているため合同記号を使った.)
　　λの位数は3^2=4, 3^3=2, 3^4=1より4だから, cは4と5の最小公倍数で20.

　　　出現点eについて考えると, あるdが存在して
　　
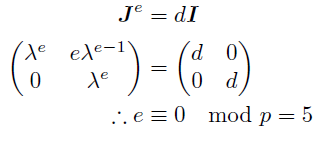
　　を満たす最小の自然数で, c=4e. 節数4.

　(ロ)a+bλ=0; b=3aのとき
　　行列の(1,2)成分からbλ^c=b. cはλの位数で4

……と, 特殊なp=5の場合もジョルダン標準形によって扱うことができた.ちなみにPを実際に求めてΦのべき乗をとるとF[n]=n・3^(n-1)と表せることがわかる.

(3)5が平方非剰余 ; p≡±3 mod 10のとき
　固有方程式はp元体の中に解を持たない. 言い換えると固有多項式はFp係数多項式環Fp[X]において既約である. そこで2次方程式の解が実数の中に存在しなかったとき虚数単位を導入したように, この固有多項式の根を「新しい数」として付け加えてしまうことを考える. 代数の言葉で言うと　X^2-X-1　の生成するイデアル(X^2-X-1)による剰余環Fp[X]/(X^2-X-1)$を考えるのだ. これは体になって, Fp上の2次元ベクトル空間, 拡大次数2の拡大体である. Xの代表する類 X+(X^2-X-1) をφとすると, φ^2-φ-1=0でこれが根の1つになる. <1,φ>はベクトル空間としての基底になり, 新しい体はFp+Fpφで表せる.
これはガロア体GF(p, 2)とも呼ばれるものである. この中で固有方程式はもう1つの解 1-φ を持つためこちらは φ* としよう. また, ここでは単純にFp^2とこの体を表すことにしよう.

　まわりくどい導入をしたが, 結局「5の平方根」をp元体上に付け加えるのと同じことである.

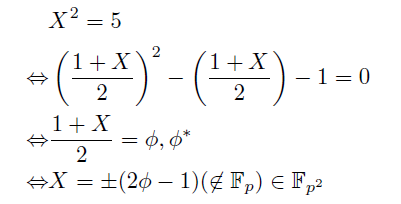
平方剰余と平方非剰余の積は平方非剰余だったから, 全ての平方非剰余がFp^2の中では異なる根を2つずつ持てることになる.

　これを使うことで, 行列ΦはFp^2上の行列として対角化することができる. 手順としては(1)の5が平方非剰余だったときとほとんど同じで, ただ単にαとβをφとφ*で置き換えれば済むので省略し, 周期cについて以下のような表し方を得る.

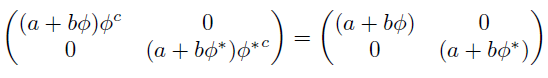
ただし今度はa+bφもa+bφ*も0とはならない. というのも, 仮に0になればaとbはともに0とはならないFpの元であるという仮定に反するためである. 1とφがFp上のベクトル空間の基底として一次独立だったことを思い出そう.

　つまり周期cは全ての系列でφとφ*の, 今度はFp^2の乗法群での位数の最小公倍数ということになる.

　出現点と周期の関係については短い周期の系列が現れない点のみ異なり, ほかは(1)と同様.

　ちなみに「p≡±3 mod 10のとき一般フィボナッチ数列の周期はフィボナッチ数列の周期に一致する」という命題はアメリカの数学者ドナルド・ウォールの名前から「ウォールの定理」と呼ばれるらしい.

　なお以下のようにして命題(II)が再度示される.
Fp^2の乗法群は元の個数が p^2-1 の巡回群であるから,

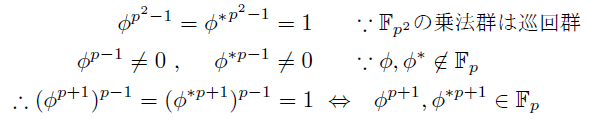
一方,

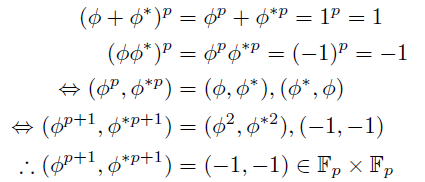
よって,

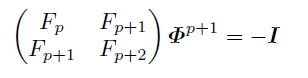
が言える.
これはφとφ*の位数が2(p+1)で割り切れ, (p+1)ではないことも意味する.

結論

　以上の考察から出現点による系列の分類ができた. まとめると, 出現点e, 周期c, (0,1)系列の節数eについて以下の関係が成り立つ. 周期が系列に依存する値であることに注意.

奇素数pに対して

• p≠5のとき
  • e ≡ ±1 mod 4 のとき全系列でc=4e, s=4
  • e ≡ 0 mod4 のとき全系列でc=2e, s=2
  • e ≡ 2 mod4のとき
    • e≡±1 mod 10 のとき　λ^2-λ-1=0の解がFp上に2つ存在し,位数が小さいほうαに対し(a, αa)系列でc=e/2, その他の系列はc=eでs=1
    • e≡±3 mod 10 のとき 全系列でc=e, s=1

• p=5のとき

　　　e=5,s=4で,c=20の系列とc=4の系列が存在.

系列の個数については単にFp×Fpから(0,0)を除いたp^2-1の元を周期で分けていけばいい.

目標に達したのでここで終える.
ここまで来ればどれも当たり前のように思えるが, フィボナッチ数列という単純な再帰数列を通じて整数の色々な性質や代数的な構造が現れてきたことには驚かされる. フィボナッチ数列やはりおもしろい.

　補遺でリュカ数列などについて述べる.

*1:「軌道」と言うほうがグローバルだったかもしれないが, 自分の中で「系列」で定着しすぎてしまったのでこう呼ぶ. しかしあまりローカルな言葉を生やしたくない気持ちもある.

*2:Zmは可換環だからZm上の行列から定義してもいいのだが

*3:この証明は中村滋『フィボナッチ数の小宇宙』(日本評論社, 2002年)p.215に載っている証明を部分的に変えたものである. その他この記事の多くの部分もこの本によるところが大きい.

*4:ちなみにフィボナッチ数列中に無限に素数が存在するか否かは未解決問題である(はず).

*5:これは単にdet(A)≠0を意味する.「行列式が0で無いならフィボナッチ数の周期と一致する」ということ自体はすぐに言えるがそうすると固有値が見えない.

*6:上でx^2=5の解の一方を√5として定めたが, 正負で分ける実数の場合と違ってどちらの解であるかを制限しない.

*7:一般の2階線形回帰数列を考えるときは必要になる.これについては次の記事で述べる.

一般フィボナッチ数列の周期について(1)

　祖先型の目で眺めたこの惑星は, 十分近づいても赤道と極以外に陸地が無いように見える.しかし周回軌道上でよく目を凝らせばその勘違いが, 青色と海を結びつける先入観に起因するものだと気付く. あるところでは群れをなし, またあるところでは毛羽立ち, 赤道では渦巻く白い雲の下にいくらか隠されながらも滑らかで穏やかな表面を見せるのが海洋だ.その一方で, 皺がよったようにわずかずつ異なる「青色」が縦横に走る領域があることが分かるだろう. 海に見えていた部分の3割は青い植物で覆われた大陸なのだ.

　伝統的な分類で主系列のF型星に属すこの系の太陽は我々の故郷のソルよりいくらか重く,その放つ光はやや明るい. そしてスペクトルのピークは短波長側にずれている. つまり少しだけ青い. 植物が持つクロロフィル――と相似な分子――が, もっともエネルギーに富む波長を選んでいないように見えるのはここでもどうやら同じようだ.

　といっても光合成の担い手が全て青いわけではない. やはり地球同様に植物の上陸が一度だけ起こったこの惑星では,現生の陸生青色植物の光合成色素は数億年間経った今でも高い一様性を保っている. しかし水中に目を転ずれば進化の試行錯誤の跡と多様性を見ることができるだろう. いくつもの系統樹の枝に渡って存在する単細胞の藻類は, この惑星を酸素で改造した祖先と微妙に異なる多様な光合成色素を持ち, 淡水海水に限らずあらゆる水圏で食物連鎖を支えていた. カルシウムの骨格を獲得したある藻類のグループはほとんど黒に近い紺色で, 浅瀬の動物に住処を与え生態系にとって重要な役割を果たしていた.

　我々が出会った緋色藻は, 高緯度地域の湖で赤く小さな体を漂わせる,そんな多くの興味深い藻類の中の1つだった.

[ライブラリ＞数学＞数論＞フィボナッチ数列]

　0,1,1,2,3,5,8,13,……言わずと知れたフィボナッチ数列.少し計算すると15番目の610で初めて最後の桁が0になる.さらに根気よく計算を続けていけば最後の桁の数がある周期を持つことに気付くだろう.と言っても21番目の10946に至ってもまだ一巡りしない.そこで最後の桁の数だけで計算を続けてみよう.

0,1,1,2,3,5,8,3,1,4,5,9,4,3,7,0,7,7,4,1,5,6,1,7,8,5,3,8,1,9,
0,9,9,8,7,5,2,7,9,6,5,1,6,7,3,0,3,3,6,9,5,4,9,3,2,5,7,2,9,1,
0,1,1,…

と60番目で0, 61番目で1が出てきて以降は繰り返されることが分かる.すなわち周期は60である.*1.

　さて, 「最後の桁の数」は我々の手が10本(十進数で)の指を備えている事情から
見えているに過ぎない. 他の自然数*2
に対する剰余の周期も気になるところである.

mod 2 : 0,1,1,0,1,1,…
mod 3 : 0,1,1,2,0,2,2,1,0,1,1,….
mod 4 : 0,1,1,2,3,1,0,1,1,…
mod 5 : 0,1,1,2,3,0,3,3,1,4,0,4,4,3,2,0,2,2,4,1,0,1,1,…

こうなると更に気になるのは0,1以外から始めた場合だ.とりあえず法を素数に限るのが常套手段*3.

　上の列を見ると2,3では全ての組が尽くされているが, mod5で出てきていない組があることに気付く.探すとそれは0が出てこない周期4の列,

1,3,4,2,1,3,…

であることが分かる.これら2つでmod5は尽くされるのだ. ただし0,0,0,…は自明だからこの例に限らず除くとする.

　mod7ではどうか.

● 0, 1, 1, 2, 3, 5, 1, 6, 0, 6, 6, 5, 4, 2, 6, 1, 0, 1, …
● 0, 2, 2, 4, 6, 3, 2, 5, 0, 5, 5, 3, 1, 4, 5, 2, 0, 2, …
● 0, 3, 3, 6, 2, 1, 3, 4, 0, 4, 4, 1, 5, 6, 4, 3, 0, 3, …

これで7*7-1個の2つ組は尽くされた.

　mod11では?

● 0, 1, 1, 2, 3, 5, 8, 2, 10, 1, 0, 1, …
● 0, 2, 2, 4, 6, 10, 5, 4, 9, 2, 0, 2, …
● 0, 3, 3, 6, 9, 4, 2, 6, 8, 3, 0, 3, …
● 0, 4, 4, 8, 1, 9, 10, 8, 7, 4, 0, 4,…
● 0, 5, 5 ,10, 4, 3, 7, 10, 6, 5, 0, 5,…
● 0, 6, 6, 1, 7, 8, 4, 1, 5, 6, 0, 6, …
● 0, 7, 7, 3, 10, 2, 1, 3, 4, 7, 0, 7, …
● 0, 8, 8, 5, 2, 7, 9, 5, 3, 8, 0, 8, …
● 0, 9, 9, 7, 5, 1, 6, 7, 2, 9, 0, 9, …
● 0, 10, 10, 9, 8, 6, 3, 9, 1, 10, 0, 10, …

0の入る場合はこれで全てだ. しかし周期10*10=100組だけしか入っていない.
11*11のマス目に印を付けてみると, 出てこない組が分かる.

● 1, 4, 5, 9, 3, 1, 4, …
● 1, 8, 9, 6, 4, 10, 3, 2, 5, 7, 1, 8, …
● 2, 8, 10, 7, 6, 2, 8, …

周期5+10+5=20組. これで全てだ.

　mod13では

● 0, 1, 1, 2, 3, 5, 8, 0, 8, 8, 3, 11, 1, 12, 0, 12, 12, 11, 10, 8, 5, 0, 5, 5, 10, 2, 12, 1, 0, 1, …
● 0, 2, 2, 4, 6, 10, 3, 0, 3, 3, 6, 9, 2, 11, 0, 11, 11, 9, 7, 3, 10, 0, 10, 10, 7, 4, 11, 2, 0, 2, …
● 0, 4, 4, 8, 12, 7, 6, 0, 6, 6, 12, 5, 4, 9, 0, 9, 9, 5, 1, 6, 7, 0, 7, 7, 1, 8, 9, 4, 0, 4, …

0を含む列は周期28が3つ, ここに入る2つ組は84. 0を含まないものは

● 2, 1, 3, 4, 7, 11, 5, 3, 8, 11, 6, 4, 10, 1, 11, 12, 10, 9, 6, 2, 8, 10, 5, 2, 7, 9, 3, 12, 2, 1, …
● 4, 2, 6, 8, 1, 9, 10, 6, 3, 9, 12, 8, 7, 2, 9, 11, 7, 5, 12, 4, 3, 7, 10, 4, 1, 5, 6, 11, 4, 2, …
● 8, 4, 12, 3, 2, 5, 7, 12, 6, 5, 11, 3, 1, 4, 5, 9, 1, 10, 11, 8, 6, 1, 7, 8, 2, 10, 12, 9, 8, 4, …

周期28が3つ. 0を含むものと同じ形だ.

　観察のため, mod17, 19も続けてみる.

mod17

0を含むもの
●0, 1, 1, 2, 3, 5, 8, 13, 4, 0, 4, 4, 8, 12, 3, 15, 1, 16, 0, 16, 16, 15, 14, 12, 9, 4, 13, 0, 13, 13, 9, 5, 14, 2, 16, 1, …
●0, 2, 2, 4, 6, 10, 16, 9, 8, 0, 8, 8, 16, 7, 6, 13, 2, 15, 0, 15, 15, 13, 11, 7, 1, 8, 9, 0, 9, 9, 1, 10, 11, 4, 15, 2, …
●0, 3, 3, 6, 9, 15, 7, 5, 12, 0, 12, 12, 7, 2, 9, 11, 3, 14, 0, 14, 14, 11, 8, 2, 10, 12, 5, 0, 5, 5, 10, 15, 8, 6, 14, 3, …
●0, 6, 6, 12, 1, 13, 14, 10, 7, 0, 7, 7, 14, 4, 1, 5, 6, 11, 0, 11, 11, 5, 16, 4, 3, 7, 10, 0, 10, 10, 3, 13, 16, 12, 11, 6, …
周期36*4列.

0を含まないもの
●1, 3, 4, 7, 11, 1, 12, 13, 8, 4, 12, 16, 11, 10, 4, 14, 1, 15, 16, 14, 13, 10, 6, 16, 5, 4, 9, 13, 5, 1, 6, 7, 13, 3, 16, 2, …
●1, 4, 5, 9, 14, 6, 3, 9, 12, 4, 16, 3, 2, 5, 7, 12, 2, 14, 16, 13, 12, 8, 3, 11, 14, 8, 5, 13, 1, 14, 15, 12, 10, 5, 15, 3, …
●1, 7, 8, 15, 6, 4, 10, 14, 7, 4, 11, 15, 9, 7, 16, 6, 5, 11, 16, 10, 9, 2, 11, 13, 7, 3, 10, 13, 6, 2, 8, 10, 1, 11, 12, 6, …
●1, 9, 10, 2, 12, 14, 9, 6, 15, 4, 2, 6, 8, 14, 5, 2, 7, 9, 16, 8, 7, 15, 5, 3, 8, 11, 2, 13, 15, 11, 9, 3, 12, 15, 10, 8, …
周期36*4列.

mod19

0を含むもの
●0, 1, 1, 2, 3, 5, 8, 13, 2, 15, 17, 13, 11, 5, 16, 2, 18, 1, …
●0, 2, 2, 4, 6, 10, 16, 7, 4, 11, 15, 7, 3, 10, 13, 4, 17, 2, …
●0, 3, 3, 6, 9, 15, 5, 1, 6, 7, 13, 1, 14, 15, 10, 6, 16, 3, …
●0, 4, 4, 8, 12, 1, 13, 14, 8, 3, 11, 14, 6, 1, 7, 8, 15, 4, …
●0, 5, 5, 10, 15, 6, 2, 8, 10, 18, 9, 8, 17, 6, 4, 10, 14, 5, …
●0, 6, 6, 12, 18, 11, 10, 2, 12, 14, 7, 2, 9, 11, 1, 12, 13, 6, …
●0, 7, 7, 14, 2, 16, 18, 15, 14, 10, 5, 15, 1, 16, 17, 14, 12, 7, …
●0, 8, 8, 16, 5, 2, 7, 9, 16, 6, 3, 9, 12, 2, 14, 16, 11, 8, …
●0, 9, 9, 18, 8, 7, 15, 3, 18, 2, 1, 3, 4, 7, 11, 18, 10, 9, …
●0, 10, 10, 1, 11, 12, 4, 16, 1, 17, 18, 16, 15, 12, 8, 1, 9, 10, …
●0, 11, 11, 3, 14, 17, 12, 10, 3, 13, 16, 10, 7, 17, 5, 3, 8, 11, …
●0, 12, 12, 5, 17, 3, 1, 4, 5, 9, 14, 4, 18, 3, 2, 5, 7, 12, …
●0, 13, 13, 7, 1, 8, 9, 17, 7, 5, 12, 17, 10, 8, 18, 7, 6, 13, …
●0, 14, 14, 9, 4, 13, 17, 11, 9, 1, 10, 11, 2, 13, 15, 9, 5, 14, …
●0, 15, 15, 11, 7, 18, 6, 5, 11, 16, 8, 5, 13, 18, 12, 11, 4, 15, …
●0, 16, 16, 13, 10, 4, 14, 18, 13, 12, 6, 18, 5, 4, 9, 13, 3, 16, …
●0, 17, 17, 15, 13, 9, 3, 12, 15, 8, 4, 12, 16, 9, 6, 15, 2, 17, …
●0, 18, 18, 17, 16, 14, 11, 6, 17, 4, 2, 6, 8, 14, 3, 17, 1, 18, …
周期18*18列

0を含まないもの
●1, 5, 6, 11, 17, 9, 7, 16, 4, …
●1, 15, 16, 12, 9, 2, 11, 13, 5, 18, 4, 3, 7, 10, 17, 8, 6, 14, …
●2, 10, 12, 3, 15, 18, 14, 13, 8, …
周期9が2つ, 周期18が1つ.

こうして課題が見えてきた.
- 周期を決めるのは何か?
- 0が初めて現れるのはいつか?
- 0を含まない系列があるのはいかなる場合か?
- 0を含むとすれば循環節中にいくつ含むか?
- 他より短い周期の系列が生じるのはいつか?

　(0,1)から始まる系列において0が初めて出てくる番号は出現点(エントリーポイント)と呼ばれ, 周期と同様に重要である.また, 0を含む系列が1つ存在すれば, 各成分に対してある数をかけることで他の系列が全て得られることはほとんど明らかだろう.このことを踏まえ, 愚直にp*pのマス目にチェックを入れながら各系列について計算する方法で上の
項目についてもっと調べてみよう.

法p	0を含む系列	周期	出現点	0の数	0を含まない系列
2	1	3	3	1	0
3	1	8	4	2	0
5	1	20	5	4	1
7	3	16	8	2	0
11	10	10	10	1	2+1
13	3	28	7	4	3
17	4	36	9	4	4
19	18	18	18	1	2+1
23	11	48	24	2	0
29	28	14	14	1	32+2
31	30	30	30	1	2+1
37	9	76	19	4	9
41	20	40	20	2	22
43	21	88	44	2	0
47	23	32	16	2	46
53	13	108	27	4	13
59	58	58	58	1	2+1
61	15	60	15	4	47
67	33	136	68	2	0
71	70	70	70	1	2+1
73	18	148	37	4	18
79	78	78	78	1	2+1
83	41	168	84	2	0
89	22	44	11	4	158
97	24	196	49	4	24

　「0を含まない系列」の項の"+1","+2"は短い周期のものがその数だけ現れていることを示す. 表には書いていないが,その長さは他の系列のちょうど半分になっている.つまり短い系列はそれほどたくさん現れずどうやらその長さは他の半分らしい.

　……ただしp=5の場合は他とは異なる. 上で見たように, 0を4つ含む周期20の系列と1,3,4,2,…の周期4の系列が現れる. これは端的に5という数がフィボナッチ数において特殊な役割を果たしていることを表している.

　今から示していくのは, 実は出現点さえ分かればこの表の他の項目は埋められるということだ. p*pのマス目を埋めていく必要はないのだ.

　そのためにフィボナッチ数について定義や重要ないくつかの命題をまとめよう.

定義1.1 フィボナッチ数列{F[n]}とは,

によって定まる再帰数列である.

　この定義では添え字は非負整数に限っているが負数番への拡張は容易だ.単にn<0に対してはF[n]=F[n+2]-F[n+1]とすればいい. そして単に偶数番に負号が付くだけであることもすぐに分かる.一応命題として述べておこう.

命題1.1　n>0に対して

　しかし初項が(0,1)だけではあまりに窮屈だ.同じ形の再帰数列を, 初項を一般の整数の組にも拡げて「一般フィボナッチ数列」とまとめて呼ぼう.

定義1.2 初項が(a,b)∈Z^2の一般フィボナッチ数列{G[n]}を

によって定める.

　後に分かることだが, a=2, b=1の場合はフィボナッチ数列と「対」になると言える重要な数列である.これをリュカ数列*4と呼ぶ.

定義1.3
リュカ数列[L[n]}とは

によって定まる数列である.

最初の数項は2,1,3,4,7,11,18,29,…となる.

　さて, 一般フィボナッチ数列も何項か計算してみればすぐにその規則に気付くだろう.

a, b, a+b, a+2b, 2a+3b, 3a+5b, …

係数にフィボナッチ数が現れている. これを命題として述べよう.

命題1.2　初項(a,b)の一般フィボナッチ数列{G[n]}に対して

証明は略すが数学的帰納法からすぐに示せる.

　より一般的な形として

命題1.3　

さらにここから系として

命題1.4

も簡単に示される.

　この関係式から感じられるように, フィボナッチ数列は行列を使うと見通しが良くなる.線型回帰数列であるから当然のことではある.簡単のためこの2つ組を「進める」行列に記号Fを当てておき以後断りなく使う.

命題1.5
行列Φ,横ベクトルg[n]を以下のように定めると次の関係式が成り立つ.

さらに行列G[n]を定めると,　

特に,

ベクトルに対して後ろから行列を書ける形式にしたのは横ベクトルで使いたいことが理由で, 特に深い意味は無い.

行列式を比較することから次の命題が得られる.

命題1.6

3番目の等式はシムソンの等式と呼ばれている*5.

　この行列Fの対角化と累乗により次の有名な等式、ビネーの公式*6*7が得られる.

命題1.7(ビネーの公式)

λ^2-λ-1の2つの解をα,βとすると,

リュカ数列に対しても同様の等式が得られる.

命題1.8

　今でこそ当たり前の公式だが, やはり整数しか出てこない数列の一般項を無理数のべき乗の線形和で表せてしまうというのは驚きである. これが整数になることはもちろん帰納法からすぐに示せるが, 有理数であることなら「直接」示せるだろう. αとβのべき乗を足すと√5が「消える」ことを言えばよいのだ. そのために二項定理を使う.

　これはカタランの公式と呼ばれるものである.

命題1.9(カタランの公式)

　リュカ数についても同様の式が成り立つが, 特に直接用いることはないため省略.

　ここまでで以後用いるフィボナッチ数についての一般的な定義と命題については一通り述べ終えた. この準備を踏まえ, 次の記事から整除性と周期について述べる.

*1:この観察はラグランジュによるものとしてコクセター『幾何学入門』(ちくま学芸文庫)で紹介されている……もっと前から知られていそうな気はするが

*2:数論の話になるため自然数に0を含めない

*3:法10を導入にしておきながら…

*4:一般の二階線形回帰数列にも同じくフランスの数学者エドゥアール・リュカ(1842-1891)の名前が冠せられていたりするがこの名前で呼ぶ

*5:それ以前にカッシーニ、カタラン達も発見していたようである.

*6:J.P.M.ビネー(仏 1786-1856). この名で呼ばれることが多いこの公式は, しかしビネーによって「再発見」されたものに過ぎないことが今では知られているようだ. 約1世紀前にオイラー, ダニエル・ベルヌーイ, ド・モアブル達が既に得ていたらしい. このような発見者と名称の不一致は歴史上しばしば見られるが(誰が最初に言い出してどうやって広まるのだろう?), ここでは一応ビネーの公式の名で呼ぶことにする.

*7:多分発見当時は行列の対角化自体をしたわけではないと思う.