一般フィボナッチ数列の周期について(2)
(1)の続き.shironetsu.hatenadiary.com
(1)の記事で実数列としてのフィボナッチ数列について一通り説明した.
ここからは整数列としてのフィボナッチ数列の性質を見ていく.
用語の定義
そのまえに, 整除性の話を始めるために, ここから成分は特に述べない限り(指数や位数, 添え字を除いて)剰余環Zm=Z/mZで考えることにする. つまり前回定義した一般フィボナッチ数列はZm上の数列に, 行列ΦやGはZmに成分を持つ2×2行列の集合M(2;Zm)の元として扱うことになる. 等号はZmでの等号の意味で使うものと実数としての等号が混在することになるが, 文脈からどちらの意味か分かるようになっている(はず).
これを踏まえ, まず「周期」や「系列」の意味をはっきりさせてしまおう.
定義2.1
一般フィボナッチ数列{G[n]}の周期cは全てのnに対して
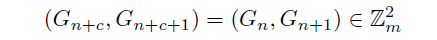
を満たす最小の自然数である.
このように定義すれば当然その存在性が問題になるが, 鳩の巣論法と,Zm上一般フィボナッチ数列の2つ組が前後に一対一であることから明らかだろう. また, 行列でこれと同値な定義を与えるとその意味は一層明確になる.

ΦがZm上可逆であることから結局周期とはこの最後の式を満たす最小の自然数であることが分かる. また, 同様の式を満たす自然数が全てcの倍数であり, その逆も成り立つこともほぼ明らかだろう.
同様に出現点についても定義しておく.
定義2.2
出現点eとは, F[e]=0 を満たす最小の自然数である.
出現点の存在性は周期が存在することから明らかである. ただしこちらにはF[e+1]についての制約が無い.
フィボナッチ数列では剰余について0を挟んだ両側は等しくなるから,行列を使って次のように言い換えることもできる.
出現点eとは, あるa≠0が存在して
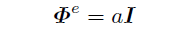
となる最小の自然数である.ただしIは単位行列.
注意すべきことは, 周期cは初項に依存するものであるのに対して出現点は(0,1)から始まるフィボナッチ数列にのみ意味を持つことだ. 思い出しておくと, この記事で述べることはその出現点, フィボナッチ数列で最初に0が出てくる番号さえ分かれば他の系列についても大体の性質が分かるということだった.
定義2.3
(a,b)∈Zm×Zmに対して, (a,b)系列*1とは
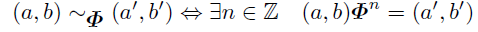
によって定まるZm×Zm上の同値関係"~Φ"による同値類である.
一応順序をなくした同値類として「系列」の意味を定めたが, 1つ代表元を取ってΦをかければすぐに復元できる. また, この言葉を使うと周期は系列の元の個数ということになる.
ところで0を含む系列と含まない系列があることを見たのだった. これらをそれぞれ「節有り」と「節無し」と呼び, 1周期の中に0を含む数を「節数」と呼ぼう.
定義2.4
(0,0)系列でない(a,b)系列Cの節数sとは
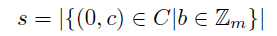
によって定まる非負整数である. このとき節有り系列は s>0 の系列であり, 節無し系列とは s=0 の系列である.
この記事で使う言葉についての定義はこれで終わった.
p元体上の一般フィボナッチ数列
一応一般の自然数に対して以上の用語を定めたが, ここからは専ら法は素数に限ることにする. そうするのはpに対して剰余環Zpがp元体(有限素体ともいう;記号Fpを使う)になって格段に調べやすくなるからに他ならない.
目標としてここで証明することを先に掲げてしまおう.
以下でpは5以外の奇素数とする.
(I) p≡±1 mod 10のとき F[p-1]≡0, F[p]≡1 mod p
p≡±3 mod 10のとき F[p]≡-1, F[p+1]≡0 mod p
(II)出現点eと節有り系列の節数sについて,
e≡0 mod 4のとき s=2
e≡±1 mod4 となるのは p≡1 mod 4のときに限り, s=4
e≡2 mod 4のときs=1
なお, 節有り系列の節数は全て一致している.
(III)p≡±3 mod10,またはe≡0,1 mod 4のとき
(0,0)系列を除く全ての系列の周期は(0,1)系列の周期に一致する.
p≡±1 mod10かつe≡2 mod 4のとき(0,0)系列を除いて
(0,1)系列の周期cより短い周期の系列が存在し, その周期はc/2
これらを使えば前回の記事の表が, 出現点を調べるだけで書けてしまう.
行列を使った表記については既に述べてきたが, ここからの話はp元体Fp上の2次正方行列が「主役」を演じることになる. *2
「系列」はFp×Fp上の同値関係から定められていたが, その中の元(a,b)と次のFp上の2次正方行列Aとの全単射により, 行列間の同値関係が誘導される.
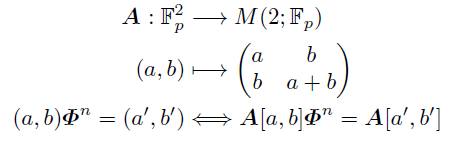
さらにこの行列をよく見ると,
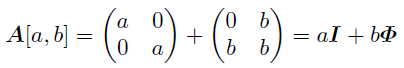
と分解できることが分かる. なお行列Aは以降もこの意味で用いることにする.
この関係からさらに興味深い構造が見えてくるが, とりあえずは素朴な数論から
示すべきことについて述べていこう.
まず周期と出現点,節の関係について簡単だが重要な関係を示す.
命題2.1
奇素数pに対して, (0,1)系列の周期cと出現点e,節数sについて
c=seで, s=1,2,4のいずれか.
(0,1)系列がフィボナッチ数列に対応することに注意.
証明
(0,1)系列の周期は
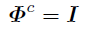
を満たす最小の自然数であり, また出現点eはあるa∈Fpが存在して
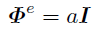
を満たす最小の自然数である.
cをeで割りc=qe+r (0≦r<e)とすると
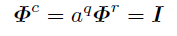
r≠0だとeの定義に反するためr=0でcはeの倍数. さらにqはa^q=1を満たす最小の自然数になる. F^e=aI, F^2e=a^2I,…,F^qe=Iよりqは節数sになるため, c=se. eとaの関係について, 行列式を比較すると,(-1)^e=a^2
(1)eが奇数のとき
a^2=-1から a≠1, a^2=-1≠1, a^3≠1, a^4=1よりs=4.
(ii)eが偶数のとき
a^2=1より a=1またはa=-1. よってs=1,2
(証明終)
「F[e]=0ならF[4e+1]=1」はもっと素朴に示すこともできる.
フィボナッチ数の「加法定理」から,
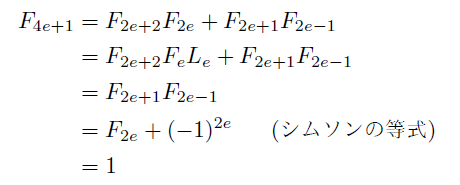
行列で計算すればすっきりするところをまわりくどくやっているだけではあるが,
フィボナッチ数列の関係式に立ち返ってみるのも悪くはない.
上で定義した行列A[a,b]の行列式は, 系列を分類する上では本質的な意味を持つ. 同じ系列に含まれるという意味で同値な2つのFp×Fpの元は, 対応する行列式が等しいかちょうど(-1)倍になっている. (a,0)が含まれる系列では, 対応する行列式は±a^2であるから,(b,0)もまた含まれるならb^2=±a^2でなければならない. そのためこれを満たすbはaを含めて高々4個に制限されることになる.
これで目標に掲げた(II)は部分的に示されたことになる. 先に示してしまったのは, 簡単なため.
では目標に掲げた(I)を示そう.
カタランの公式を思い出すと, 奇素数pに対してp番目のフィボナッチ数は,
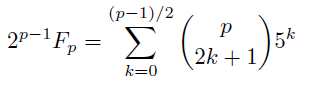
ただし今度の等号はp元体の元としての意味である. フェルマーの小定理から2^{p-1}=1, さらに2項係数について
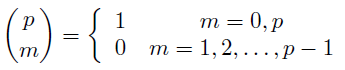
の関係を思い出すと,
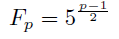
再びフェルマーの小定理からこの値は±1であることは分かるが, そのどちらだろうか.ここで登場するのがルジャンドル記号である. つまり平方剰余が関わってくることになる.
平方剰余
数論の基本的な内容ではあるが, 極めて重要なため平方剰余について一通り述べておこう. ここでは合同式の記号を使うことにする. またpは奇素数とする.
定義2.5
pの倍数でないaに対して x^2≡a mod pを満たす整数xが存在するとき, aを(pに対する)平方剰余, 存在しないとき平方非剰余という.
たとえば7に対して
1^2≡1, 2^2≡4, 3^2≡2, 4^2≡2, 5^2 ≡4, 6^2=1
から, 1,2,4は平方剰余, 3,5,6は平方非剰余である.
定義2.6
ルジャンドル記号(a/p)は
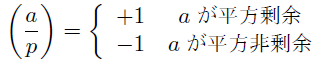
によって定められる.
法pにおいて平方剰余と平方非剰余はともに(p-1)/2個ずつ存在する.
命題2.2
ルジャンドル記号に対して次の関係が成立する.ここでa,bはpの倍数でない整数, pとqは相異なる奇素数とする.
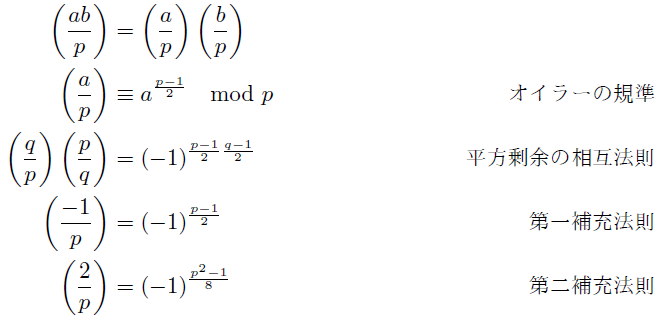
一番上の法則は
(平方剰余)×(平方剰余)=(平方剰余)
(平方非剰余)×(平方非剰余)=(平方剰余)
(平方剰余)×(平方非剰余)=(平方非剰余)
となることを言っている.
平方剰余の相互法則はいわゆる初等数論の中でもっとも重要な定理の一つで, それを認識したガウスがそのいくつもの異なる証明を与えたことで有名である.
平方剰余についてはとりあえずこれで十分. では中断していた証明に戻ろう
オイラーの規準からp元体Fpの元として
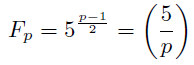
となるから, 5が平方剰余であるか否かを見ればいい. 5以外の奇素数pについて相互法則から,
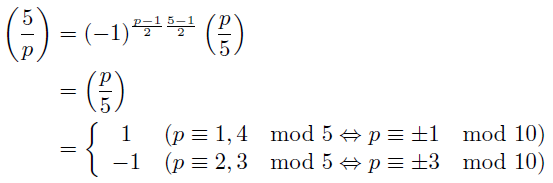
法10に置き換えられるのはpが奇数のため.
結局, 5以外の奇素数pに対して
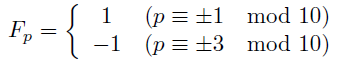
が示された.
F[p-1],F[p+1]に対しても同じようにしてpに対する剰余を求められるが, やや煩雑である. そこで行列を使った方法を試みよう. *3
Φに対して, ケーリー・ハミルトンの法則から,
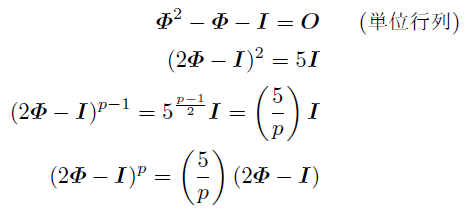
1行目から2行目で「平方完成」, 2行目から3行目で両辺(p-1)/2乗,
3行目から4行目で両辺に(2Φ-I)をかけた.
4行目の左辺を2項展開すると,
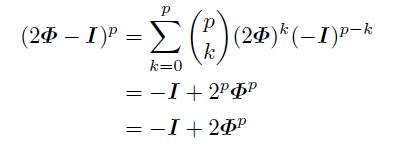
pについて場合分けすると,
(1)(5/p)=+1 ; 5が平方剰余であるとき
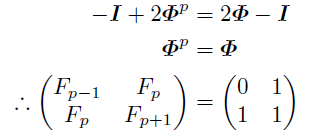
(2)(5/p)=-1; 5が平方非剰余であるとき
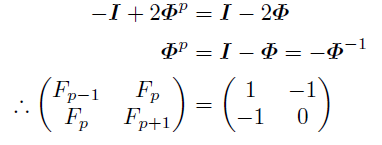
ルジャンドル記号(5/p)を使ってまとめると,
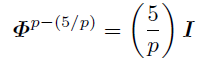
とも書ける.
この結果は重要だ. 5が平方剰余のとき出現点も周期もp-1の約数になる.5が平方非剰余のとき出現点はp+1の約数, 周期は2p+2の(p+1以外の)約数になる.表を見ればこのことが確かめられるだろう.
実は出現点そのものについて(この記事では)これ以上強い主張ができない. 前の記事の表を再び見ると, たとえばp=83では出現点はp+1=84, 周期は2p+2=168でたっぷりかかるパターンになっている. その一方p=89は11(p-1=88の約数)が出現点で, 周期も44と短い.表には載っていないが, 23番目のフィボナッチ数28657は素数であるため, 出現点23(28657+1を割り切って商は1246),周期92ともっと短い*4.
この出現点と周期の性質については後で再び別証明が与えられることを見るだろう. では続いて目標に掲げた(II)(III)についてまとめて証明に入る.
対角化, ジョルダン標準形, 体の拡大
(a,b)系列の周期cは
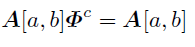
を満たす最小の自然数なのだった.
行列で表したのだからΦを対角化しよう.固有値をλとして固有方程式を求めると,
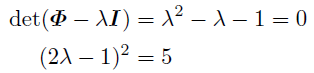
思い出さねばならないのはこれがp元体Fp上での方程式だということだ. 5が平方剰余のとき2つの異なる解が存在するが, pが平方非剰余のときFp上に解は存在せず, p=5のときは重解になる.
それぞれ場合分けして考える.
(1)5が平方剰余 ; p≡±1 mod 10のとき
x^2=5はp元体上2つの解を持つからその一方を√5と書いてしまう. このときもう一方は-√5. そして分数を分母の逆元をかける意味で使うと結局実数の時と同じように2つの固有値は
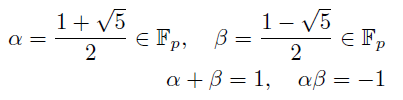
になる.2行目は解と係数の関係である.
たとえばp=19のときx^2=5の解は9,-9=10の2つで, 固有値は5,15の2つ.
対角行列Λを次のように定めて, 各固有値に対応する固有ベクトルを並べた行列Pを用いてΦを対角化できる.
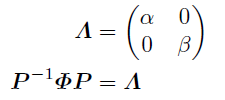
これを使ってΦのべき乗をとると周期cについて次のように書ける.
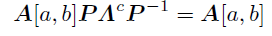
ここでA[a,b]=aI+bΦという関係があったことを思い出すと,
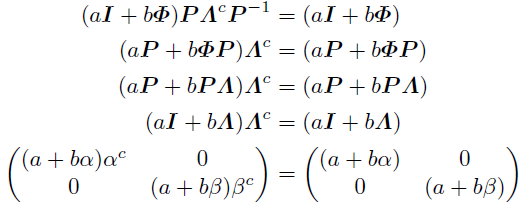
この成分を見てさらに場合分けする.
(イ)a+bα≠0かつa+bβ≠0のとき
(a+bα)(a+bβ)=a^2-ab-b^2≠0と表せて*5, cはα^c=1かつβ^c=1を満たす最小の自然数になる. ゆえにcはαとβの(Fpの乗法群での)位数の最小公約数ということになる.
(ロ)a+bα=0のとき
b=-a/α=βaで, この系列は a,βa,β^2a,β^3a… という「等比数列」になる. このときa+bβ=(2+β)a≠0(a,bがともに0とはなっていないことを仮定)だから, 周期はβの位数.
(ハ)a+bβ=0のとき
(ロ)と同様に周期はαの位数.
αとβの位数の関係を考える. 位数の大きくないほうをα,その位数をkとする.*6
(i)kが奇数のとき
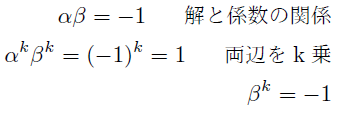
仮定よりβの位数はk以上であるため位数は2kになる. これらの公約数は2k. 結局,
a^2-ab-b^2≠0またはb=βaのとき周期2k,
b=αaのとき周期kと他のちょうど半分の長さになる.
(ii)kが偶数のとき
同様にして

仮定からβの位数はk.
a^2-ab-b^2≠0,b=αa,b=βaいずれの場合にも周期はkになる.
続けて出現点についても考える.出現点eはあるd≠0が存在して次の条件を満たす最小の自然数である.
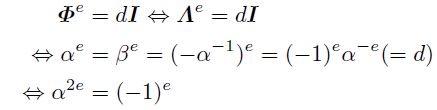
(i)eが奇数のとき
(α^e)^2=-1より-1が平方剰余になるから, 第一補充法則よりp≡1 mod 4
eはこれを満たす最小の自然数だから, αの位数はk=4e. すなわちαの位数が偶数の場合に相当し, 節数は4.
(ii)eが偶数のとき
α^2e=1となるが,α^e=-1, 1, またe≡0,2 mod 4(それぞれ自然数e'によりe=4e', e=4e'+2とおく)のときとでさらに分ける.
(ii-1) α^e=-1 かつ e≡0 mod 4のとき
k=2eでαの位数が偶数の場合に相当し, 節数は2.
(ii-2) α^e=-1 かつ e≡2 mod 4のとき
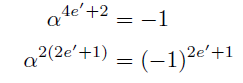
よりeの最小性に反す.
(ii-3) α^e=1 かつ e≡0 mod 4のとき
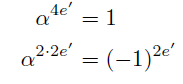
よりeの最小性に反す.
(ii-4)α^e=1 かつ e≡2 mod 4のとき
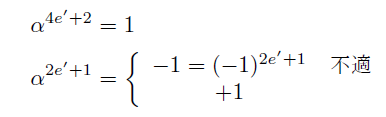
よってαの位数はk=2e'+1=e/2で, 奇数の場合に相当し節数は1
まとめると
eが奇数のときk=4e, すべての系列で周期は等しく4e, 節数4
e≡0 mod4のときk=2e, すべての系列で周期は等しく2e, 節数2
e≡2 mod4のときk=e/2, (a, αa)系列で周期e/2, その他の系列は周期eで節数1
ちなみにαとβに対してフェルマーの小定理を使うと,
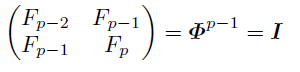
が言える.
(2)p=5のとき
1つしかないわけだからわざわざ行列で見なくてもいいが統一的に扱う*7.
固有方程式の解は
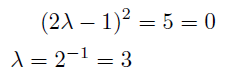
で重根を持ち対角化できないが, ジョルダン標準形には変形できる.
行列PとJが存在して, (1)と同様にして(a,b)系列の周期cを次のように表せる.
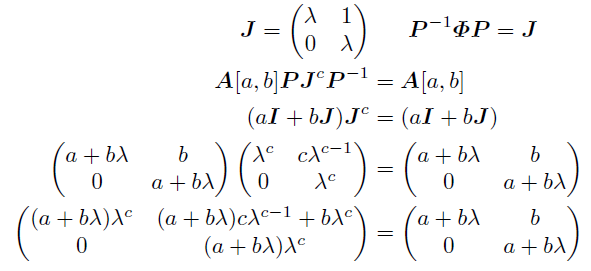
(イ)a+bλ≠0; b≠3aのとき
行列の対角成分からλ^c=1. これを代入すると(1,2)成分から
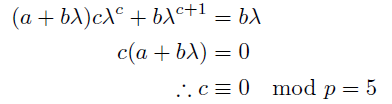
(「微分のような形」になって指数が肩から降りてきているため合同記号を使った.)
λの位数は3^2=4, 3^3=2, 3^4=1より4だから, cは4と5の最小公倍数で20.
出現点eについて考えると, あるdが存在して
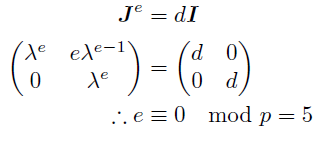
を満たす最小の自然数で, c=4e. 節数4.
(ロ)a+bλ=0; b=3aのとき
行列の(1,2)成分からbλ^c=b. cはλの位数で4
……と, 特殊なp=5の場合もジョルダン標準形によって扱うことができた.ちなみにPを実際に求めてΦのべき乗をとるとF[n]=n・3^(n-1)と表せることがわかる.
(3)5が平方非剰余 ; p≡±3 mod 10のとき
固有方程式はp元体の中に解を持たない. 言い換えると固有多項式はFp係数多項式環Fp[X]において既約である. そこで2次方程式の解が実数の中に存在しなかったとき虚数単位を導入したように, この固有多項式の根を「新しい数」として付け加えてしまうことを考える. 代数の言葉で言うと X^2-X-1 の生成するイデアル(X^2-X-1)による剰余環Fp[X]/(X^2-X-1)$を考えるのだ. これは体になって, Fp上の2次元ベクトル空間, 拡大次数2の拡大体である. Xの代表する類 X+(X^2-X-1) をφとすると, φ^2-φ-1=0でこれが根の1つになる. <1,φ>はベクトル空間としての基底になり, 新しい体はFp+Fpφで表せる.
これはガロア体GF(p, 2)とも呼ばれるものである. この中で固有方程式はもう1つの解 1-φ を持つためこちらは φ* としよう. また, ここでは単純にFp^2とこの体を表すことにしよう.
まわりくどい導入をしたが, 結局「5の平方根」をp元体上に付け加えるのと同じことである.
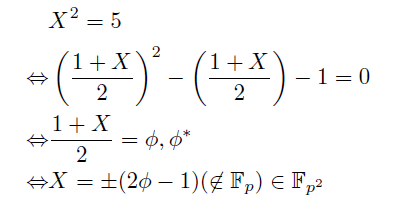
平方剰余と平方非剰余の積は平方非剰余だったから, 全ての平方非剰余がFp^2の中では異なる根を2つずつ持てることになる.
これを使うことで, 行列ΦはFp^2上の行列として対角化することができる. 手順としては(1)の5が平方非剰余だったときとほとんど同じで, ただ単にαとβをφとφ*で置き換えれば済むので省略し, 周期cについて以下のような表し方を得る.
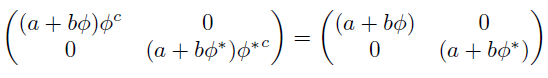
ただし今度はa+bφもa+bφ*も0とはならない. というのも, 仮に0になればaとbはともに0とはならないFpの元であるという仮定に反するためである. 1とφがFp上のベクトル空間の基底として一次独立だったことを思い出そう.
つまり周期cは全ての系列でφとφ*の, 今度はFp^2の乗法群での位数の最小公倍数ということになる.
出現点と周期の関係については短い周期の系列が現れない点のみ異なり, ほかは(1)と同様.
ちなみに「p≡±3 mod 10のとき一般フィボナッチ数列の周期はフィボナッチ数列の周期に一致する」という命題はアメリカの数学者ドナルド・ウォールの名前から「ウォールの定理」と呼ばれるらしい.
なお以下のようにして命題(II)が再度示される.
Fp^2の乗法群は元の個数が p^2-1 の巡回群であるから,
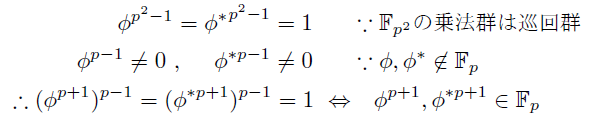
一方,
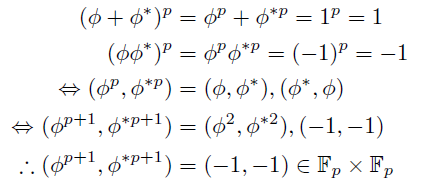
よって,
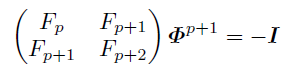
が言える.
これはφとφ*の位数が2(p+1)で割り切れ, (p+1)ではないことも意味する.
結論
以上の考察から出現点による系列の分類ができた. まとめると, 出現点e, 周期c, (0,1)系列の節数eについて以下の関係が成り立つ. 周期が系列に依存する値であることに注意.
奇素数pに対して
- p≠5のとき
- e ≡ ±1 mod 4 のとき全系列でc=4e, s=4
- e ≡ 0 mod4 のとき全系列でc=2e, s=2
- e ≡ 2 mod4のとき
- e≡±1 mod 10 のとき λ^2-λ-1=0の解がFp上に2つ存在し,位数が小さいほうαに対し(a, αa)系列でc=e/2, その他の系列はc=eでs=1
- e≡±3 mod 10 のとき 全系列でc=e, s=1
- p=5のとき
e=5,s=4で,c=20の系列とc=4の系列が存在.
系列の個数については単にFp×Fpから(0,0)を除いたp^2-1の元を周期で分けていけばいい.
目標に達したのでここで終える.
ここまで来ればどれも当たり前のように思えるが, フィボナッチ数列という単純な再帰数列を通じて整数の色々な性質や代数的な構造が現れてきたことには驚かされる. フィボナッチ数列やはりおもしろい.
補遺でリュカ数列などについて述べる.
*1:「軌道」と言うほうがグローバルだったかもしれないが, 自分の中で「系列」で定着しすぎてしまったのでこう呼ぶ. しかしあまりローカルな言葉を生やしたくない気持ちもある.
*2:Zmは可換環だからZm上の行列から定義してもいいのだが
*3:この証明は中村滋『フィボナッチ数の小宇宙』(日本評論社, 2002年)p.215に載っている証明を部分的に変えたものである. その他この記事の多くの部分もこの本によるところが大きい.
*4:ちなみにフィボナッチ数列中に無限に素数が存在するか否かは未解決問題である(はず).
*5:これは単にdet(A)≠0を意味する.「行列式が0で無いならフィボナッチ数の周期と一致する」ということ自体はすぐに言えるがそうすると固有値が見えない.
*6:上でx^2=5の解の一方を√5として定めたが, 正負で分ける実数の場合と違ってどちらの解であるかを制限しない.
*7:一般の2階線形回帰数列を考えるときは必要になる.これについては次の記事で述べる.