G2 ― ディンキン図形から7次元クロス積まで
ここに型のディンキン図形がある. 何も知らないふりをしてこの図が表すリー代数がどういう素性を持っているのか調べよう.
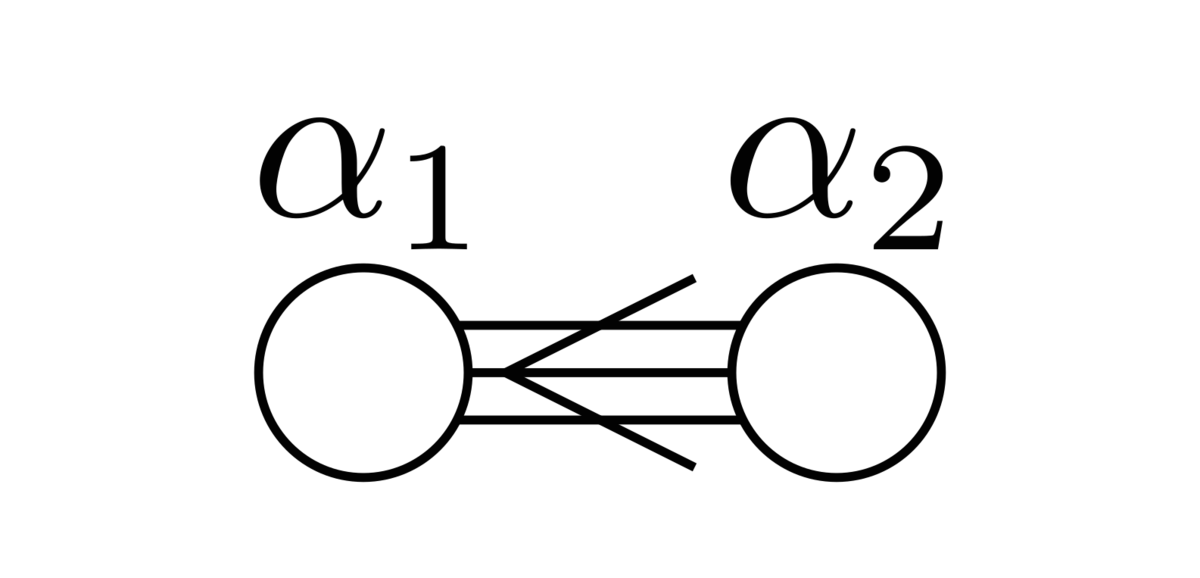
ふたつの頂点には上のように単純ルート を割り当てる. 間の線が3本なので,
\begin{align}
\frac{4(\alpha_1,\alpha_2)^2}{|\alpha_1|^2|\alpha_2|^2} = 3.
\end{align}
矢印は の向きについているから,
. 従って,
\begin{align}
\frac{2(\alpha_1,\alpha_2)}{|\alpha_2|^2} = -1,\ \ \
\frac{2(\alpha_2,\alpha_1)}{|\alpha_1|^2} = -3.
\end{align}
ここからカルタン行列 が復元される.
\begin{align}
C= \begin{pmatrix}
2 & -1\\
-3 & 2
\end{pmatrix},\ \ \
C_{ij} = \frac{2(\alpha_i,\alpha_j)}{|\alpha_j|^2}
\end{align}
続いて, ルート系全体 を復元する. 正ルートは,
\begin{align}
\begin{array}{|c|c|} \hline
\mbox{高さ} & \mbox{正ルート} \\ \hline
1 & \alpha_1,\ \alpha_2 \\ \hline
2 & \alpha_1 + \alpha_2 \\ \hline
3 & 2\alpha_1 + \alpha_2 \\ \hline
4 & 3\alpha_1 + \alpha_2 \\ \hline
5 & 3\alpha_1 + 2\alpha_2 \\ \hline
\end{array}
\end{align}
合わせて6本.
を正規直交基底にもつ2次元ユークリッド空間にルート系を埋め込もう.
と決めると,
\begin{align}
\alpha_1 = e_1,\ \ \ \alpha_2=-\frac{3}{2}e_1 + \frac{\sqrt{3}}{2}e_2
\end{align}
図にすると以下のようになる. ランクは2なので全部で14次元だと分かる.

既約表現を調べる. カルタン行列の逆を取ると,
\begin{align}
C^{-1} = \begin{pmatrix}
2 & 1\\
3 & 2
\end{pmatrix}
\end{align}
から, 基本ウェイトは,
\begin{align}
\omega_1 &= 2\alpha_1 + \alpha_2,\\
\omega_2 &= 3\alpha_1 + 2\alpha_2.
\end{align}
任意のウェイトはこの2つの基本ウェイトの整数係数線形和であって, と表せる. これを
と略記する.
最高ウェイトが であるような既約表現
の次元は, ワイルの次元公式から,
\begin{align}
{\rm dim}(V_\lambda)
=
\frac{\prod_{\alpha\in\Delta^+} (\lambda+\rho,\alpha)}
{\prod_{\alpha\in\Delta^+} (\rho,\alpha)}.
\end{align}
(参考 : Weyl character formula - Wikipedia)
ここに, は正ルート全体の集合,ワイルベクトル
は正ルート全体の和の1/2, すなわち,
\begin{align}
\rho = \frac{1}{2}\sum_{\alpha\in\Delta^+} \alpha= 5\alpha_1 + 3\alpha_2.
\end{align}
である.
\begin{gather}
\lambda = (2m_1+3m_2)\alpha_1+(m_1+2m_2)\alpha_2,\\
(\alpha_1,\alpha_1) = 1,\ (\alpha_1,\alpha_2) = -\frac{3}{2},\ (\alpha_2,\alpha_2) = 3
\end{gather}
を使って計算すると,
\begin{align}
&\prod_{\alpha\in\Delta^+} (\lambda+\rho,\alpha)\\
&=\left(\frac{1}{2}m_1+\frac{1}{2}\right)
\left(\frac{3}{2}m_2+\frac{3}{2}\right)
\left(\frac{1}{2}m_1+\frac{3}{2}m_2+2\right)
\left(m_1+\frac{3}{2}m_2+\frac{5}{2}\right)
\left(\frac{3}{2}m_1+\frac{3}{2}m_2+3\right)
\left(\frac{3}{2}m_1+3m_2+\frac{9}{2}\right)
\end{align}
これが分母. 分子はを代入して得られる.
\begin{align}
&\dim(V_\lambda)\\
&=\left(m_1+1\right)\left(m_2+1\right)
\left(\frac{1}{4}m_1+\frac{3}{4}m_2+1\right)
\left(\frac{2}{5}m_1+\frac{3}{5}m_2+1\right)
\left(\frac{1}{2}m_1+\frac{1}{2}m_2+1\right)
\left(\frac{1}{3}m_1+\frac{2}{3}m_2+1\right)
\end{align}
いくつかのに対して実際に値を求める.
\begin{align}
\begin{array}{|c|c|}\hline
(m_1,m_2) & {\rm dim} \\ \hline
(0,0) & 1\\ \hline
(1,0) & 7 \\ \hline
(0,1) & 14\\ \hline
(2,0) & 27\\ \hline
(1,1) & 64\\ \hline
(0,2) & 77\\ \hline
(3,0) & 77\\ \hline
(2,1) & 189\\ \hline
(1,2) & 286\\ \hline
(0,3) & 273\\ \hline
\end{array}
\end{align}
(参考: A104599 - OEIS 複素数上のG2型リー代数の既約表現の次元を昇順に並べた数列.)
自明表現を除けば最小の次元は7. ウェイトを求める.

長方形の中にウェイトのラベルが入っていて, 左に下がる方へ
, 右に下がる方へ
と単純ルートひとつぶん下がっていく. これを見ると, 重複度はどれも1であることが分かる.
既約表現をその次元(のボールド体)で表すことにする. つまり,最高ウェイトをに持つ既約表現は
, 最高ウェイトが
なら
という具合に.
表現同士のテンソル積(「合成系」と呼ぶ)
は対称部分と反対称部分に分けられて, それぞれ次元は
となっている.
最高ウェイトの既約表現が対称部分に含まれて, これは27次元である.従って残った1次元は自明表現.
反対称部分は最高ウェイトの既約表現を含んでいて,次元14. 随伴表現に一致するため,
を除いて重複度は2. 残された7次元は最高ウェイト
を含むので,
表現.
各空間のウェイトの重複度は以下のようになっている.
\begin{align}
\begin{array}{|c|c|c|c|c|}\hline
\mbox{ウェイト} & {\bf 27} & {\bf 1} &{\bf 14}&{\bf 7}\\ \hline
(2,0) & 1 &0& 0&0\\\hline
(0,1) & 1 &0& 1&0\\\hline
(-2,2) & 1 &0& 0&0\\\hline
(3,-1) & 1 &0& 1&0\\\hline
(1,0) & 2 &0& 1&1\\\hline
(-1,1) & 2 &0&1&1\\\hline
(4,-2) & 1 &0&0&0\\\hline
(-3,2) & 1 &0&1&0\\\hline
(2,-1) & 2 &0& 1&1\\\hline
(0,0) & 3 &1&2&1\\\hline
(-2,1) & 2 &0&1&1\\\hline
(3,-2) & 1 &0&1&0\\\hline
(-4,2) & 1 &0&0&0\\\hline
(1,-1) & 2 &0& 1&1\\\hline
(-1,0) & 2 &0& 1&1\\\hline
(-3,1) & 1 &0& 1&0\\\hline
(2,-2) & 1 &0& 0&0\\\hline
(0,-1) & 1&0&1&0\\\hline
(-2,0) & 1&0&0&0\\\hline
\end{array}
\end{align}
ふたつの7次元表現から7次元表現が出てくる. これに注目する.
実際に既約分解を行うことで詳しく調べる. 一般に, あるウェイトを持つ固有状態(量子力学ふうに)
とルート
に対して,
がウェイトであって
がウェイトでない
がウェイトであって
がウェイトでない
ような非負整数が存在する. このとき,
\begin{align}
\left|E_{-\alpha}|\mu\rangle\right|^2 = \frac{1}{2}q(p+1)(\alpha,\alpha).
\end{align}
ただし, ルートに対応するリー代数の元を
で表した.
表現のウェイト
に対応する状態を単に
で表すことにすると,
\begin{align}
E_{-\alpha1}|1,0\rangle & = \sqrt{\frac{1}{2}}|\!-\!1,1\rangle\\
E_{-\alpha2}|\!-\!1,1\rangle &= \sqrt{\frac{3}{2}}|2,\!-\!1\rangle\\
E_{-\alpha1}|2,\!-\!1\rangle &= |0,0\rangle\\
E_{-\alpha1}|0,0\rangle &= |\!-\!2,1\rangle\\
E_{-\alpha2}|\!-\!2,1\rangle &= \sqrt{\frac{3}{2}}|1,\!-\!1\rangle\\
E_{-\alpha1}|1,\!-\!1\rangle & = \sqrt{\frac{1}{2}}|\!-\!1,0\rangle\\
\end{align}
から全ての状態が得られる.
合成系はで表すことにする. まずは
表現を見る.
\begin{align}
|{\bf 14},0,1\rangle\!\rangle
&= \sqrt{\frac{1}{2}}
\Big(|1,0\rangle|\!-\!1,1\rangle-|\!-\!1,1\rangle|1,0\rangle\Big)\\
|{\bf 14},3,-1\rangle\!\rangle
&= \sqrt{\frac{2}{3}}E_{-\alpha2}|{\bf 14},0,1\rangle\!\rangle\\
&= \sqrt{\frac{2}{3}}
\sqrt{\frac{1}{2}}
\Big(|1,0\rangle\sqrt{\frac{3}{2}}|2,\!-\!1\rangle
-\sqrt{\frac{3}{2}}|2,\!-\!1\rangle|1,0\rangle\Big)\\
&=\sqrt{\frac{1}{2}}
\Big(|1,0\rangle|2,\!-\!1\rangle
-|2,\!-\!1\rangle|1,0\rangle\Big)\\
|{\bf 14},1,0\rangle\!\rangle &=\sqrt{\frac{2}{3}}E_{-\alpha1}|{\bf 14},3,-1\rangle\!\rangle\\
&=\sqrt{\frac{2}{3}}
\sqrt{\frac{1}{2}}
\Big(\sqrt{\frac{1}{2}}|\!-\!1,1\rangle|2,\!-\!1\rangle
+|1,0\rangle|0,0\rangle
-|0,0\rangle|1,0\rangle
-|2,\!-\!1\rangle\sqrt{\frac{1}{2}}|\!-\!1,1\rangle\Big)\\
&=\sqrt{\frac{1}{6}}\Big(|\!-\!1,1\rangle|2,\!-\!1\rangle-|2,\!-\!1\rangle|\!-\!1,1\rangle\Big)
+\sqrt{\frac{1}{3}}\Big(|1,0\rangle|0,0\rangle-|0,0\rangle|1,0\rangle\Big).
\end{align}
合成系の反対称部分のウェイトの空間は2次元なので,この中で
に直交するベクトルを取ればそれを
と決められる.
\begin{align}
|{\bf 7},1,0\rangle\!\rangle
= -\sqrt{\frac{1}{3}}\Big(|\!-\!1,1\rangle|2,\!-\!1\rangle-|2,\!-\!1\rangle|\!-\!1,1\rangle\Big)
+\sqrt{\frac{1}{6}}\Big(|1,0\rangle|0,0\rangle-|0,0\rangle|1,0\rangle\Big)
\end{align}
これを次々に下降させて合成系の表現全体を得る.
\begin{align}
|{\bf 7},-1,1\rangle\!\rangle
&=\sqrt{2}E_{-\alpha1}|{\bf 7},1,0\rangle\!\rangle\\
&=-\sqrt{\frac{1}{6}}\Big(|\!-\!1,1\rangle|0,0\rangle-|0,0\rangle|\!-\!1,1\rangle\Big)
+\sqrt{\frac{1}{3}}\Big(|1,0\rangle|\!-\!2,1\rangle-|\!-\!2,1\rangle|1,0\rangle\Big)\\
|{\bf 7},2,\!-\!1\rangle\!\rangle
&=\sqrt{\frac{2}{3}}E_{-\alpha2}|{\bf 7},-1,1\rangle\!\rangle\\
&=-\sqrt{\frac{1}{6}}\Big(|2,\!-\!1\rangle|0,0\rangle-|0,0\rangle|2,\!-\!1\rangle\Big)
+\sqrt{\frac{1}{3}}\Big(|1,0\rangle|1,\!-\!1\rangle-|1,\!-\!1\rangle|1,0\rangle\Big)\\
|{\bf 7},0,0\rangle\!\rangle
&=E_{-\alpha1}|{\bf 7},2,\!-\!1\rangle\!\rangle\\
&=-\sqrt{\frac{1}{6}}\Big(|2,-1\rangle|-2,1\rangle-|-2,1\rangle|2,-1\rangle\Big)\\
&+\sqrt{\frac{1}{6}}\Big(|-1,1\rangle|1,-1\rangle-|1,-1\rangle|-1,1\rangle\Big)
+\sqrt{\frac{1}{6}}\Big(|1,0\rangle|-1,0\rangle-|-1,0\rangle|1,0\rangle\Big)\\
|{\bf 7},-2,1\rangle\!\rangle
&=E_{-\alpha1}|{\bf 7},0,0\rangle\!\rangle\\
&=-\sqrt{\frac{1}{6}}\Big(|0,0\rangle|-2,1\rangle-|-2,1\rangle|0,0\rangle\Big)
+\sqrt{\frac{1}{3}}\Big(|-1,1\rangle|-1,0\rangle-|-1,0\rangle|-1,1\rangle\Big)\\
|{\bf 7},1,-1\rangle\!\rangle
&=\sqrt{\frac{2}{3}}E_{-\alpha1}|{\bf 7},-2,1\rangle\!\rangle\\
&=-\sqrt{\frac{1}{6}}\Big(|0,0\rangle|1,-1\rangle-|1,-1\rangle|0,0\rangle\Big)
+\sqrt{\frac{1}{3}}\Big(|2,-1\rangle|-1,0\rangle-|-1,0\rangle|2,-1\rangle\Big)\\
|{\bf 7},-1,0\rangle\!\rangle
&=\sqrt{2}E_{-\alpha1}|{\bf 7},1,-1\rangle\!\rangle\\
&=-\sqrt{\frac{1}{3}}\Big(|-2,1\rangle|1,-1\rangle-|1,-1\rangle|-2,1\rangle\Big)
+\sqrt{\frac{1}{6}}\Big(|0,0\rangle|-1,0\rangle-|-1,0\rangle|0,0\rangle\Big)
\end{align}
よく見るとだけ位置付けが明らかに異なっている. これを解消するためにユニタリ変換で
表現の基底を取り換える.
\begin{align}
|1,0\rangle &= \frac{-|1\rangle-i|7\rangle}{\sqrt{2}}\\
|-1,1\rangle &= \frac{i|2\rangle+|6\rangle}{\sqrt{2}}\\
|2,-1\rangle &= \frac{-|3\rangle-i|5\rangle}{\sqrt{2}}\\
|0,0\rangle &= -|4\rangle\\
|-2,1\rangle &= \frac{|3\rangle-i|5\rangle}{\sqrt{2}}\\
|1,-1\rangle &= \frac{-i|2\rangle+|6\rangle}{\sqrt{2}}\\
|1,0\rangle &= \frac{|1\rangle-i|7\rangle}{\sqrt{2}}
\end{align}
すると,
\begin{align}
|{\bf 7},1\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|2\rangle|3\rangle+|3\rangle|2\rangle
+|4\rangle|7\rangle+|5\rangle|6\rangle
-|6\rangle|5\rangle-|7\rangle|4\rangle\Big)\\
|{\bf 7},2\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(|1\rangle|3\rangle-|3\rangle|1\rangle
+|4\rangle|6\rangle-|5\rangle|7\rangle
-|6\rangle|4\rangle+|7\rangle|5\rangle\Big)\\
|{\bf 7},3\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|1\rangle|2\rangle+|2\rangle|1\rangle
-|4\rangle|5\rangle+|5\rangle|4\rangle
-|6\rangle|7\rangle+|7\rangle|6\rangle\Big)\\
|{\bf 7},4\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|1\rangle|7\rangle-|2\rangle|6\rangle
+|3\rangle|5\rangle-|5\rangle|3\rangle
+|6\rangle|2\rangle+|7\rangle|1\rangle\Big)\\
|{\bf 7},5\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|1\rangle|6\rangle+|2\rangle|7\rangle
-|3\rangle|4\rangle+|4\rangle|3\rangle
+|6\rangle|1\rangle-|7\rangle|2\rangle\Big)\\
|{\bf 7},6\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(|1\rangle|5\rangle+|2\rangle|4\rangle
+|3\rangle|7\rangle-|4\rangle|2\rangle
-|5\rangle|1\rangle-|7\rangle|3\rangle\Big)\\
|{\bf 7},7\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(|1\rangle|4\rangle-|2\rangle|5\rangle
-|3\rangle|6\rangle-|4\rangle|1\rangle
+|5\rangle|2\rangle+|6\rangle|3\rangle\Big)
\end{align}
ときれいになる. 更に置換の巡回記法でと数字を入れ替えて(きわめて恣意的だが...),
\begin{align}
|{\bf 7},1\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(|2\rangle|3\rangle-|3\rangle|2\rangle+|4\rangle|5\rangle
-|5\rangle|4\rangle+|6\rangle|7\rangle-|7\rangle|6\rangle\Big)\\
|{\bf 7},2\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|1\rangle|3\rangle+|3\rangle|1\rangle
-|4\rangle|6\rangle+|5\rangle|7\rangle+|6\rangle|4\rangle-|7\rangle|5\rangle\Big)\\
|{\bf 7},3\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(+|1\rangle|2\rangle-|2\rangle|1\rangle+|4\rangle|7\rangle
+|5\rangle|6\rangle-|6\rangle|5\rangle
-|7\rangle|4\rangle\Big)\\
|{\bf 7},4\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|1\rangle|5\rangle+|2\rangle|6\rangle-|3\rangle|7\rangle
+|5\rangle|1\rangle-|6\rangle|2\rangle
+|7\rangle|3\rangle\Big)\\
|{\bf 7},5\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(|1\rangle|4\rangle-|2\rangle|7\rangle-|3\rangle|6\rangle
-|4\rangle|1\rangle+|6\rangle|3\rangle+|7\rangle|2\rangle\Big)\\
|{\bf 7},6\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(-|1\rangle|7\rangle-|2\rangle|4\rangle+|3\rangle|5\rangle
+|4\rangle|2\rangle-|5\rangle|3\rangle+|7\rangle|1\rangle\Big)\\
|{\bf 7},7\rangle\!\rangle
&=\frac{i}{\sqrt{6}}\Big(|1\rangle|6\rangle+ |2\rangle|5\rangle+|3\rangle|4\rangle-|4\rangle|3\rangle-|5\rangle|2\rangle
-|6\rangle|1\rangle
\Big)
\end{align}
を得る.
定数倍を無視するとこれは7次元クロス積に他ならない.
Seven-dimensional cross product - Wikipedia
...........................
は八元数の自己同型群として知られる. 実部は不変なので,
への作用で7次元クロス積の自己同型群と考えてもいい. この事実からルート系を決めるまでは横田一郎『例外型単純リー群』(現代数学社)第1章に詳しく書かれている.
Ichiro Yokota "Exceptional Lie groups"
https://arxiv.org/abs/0902.0431
では逆に八元数なんて知らないふりをして, ディンキン図から「八元数の自己同型群」であることを知ることができるか...というと上にやった通り. 原理的には手順はほぼ決まっているので計算を頑張るだけではある. ここでやったのは7次元クロス積が出てくるまでなので微妙に届いていないが, もう少し頑張ると1次元表現から7次元ノルムが出てきて八元数そのものが見えてくるはず.
型についても複雑怪奇なベクトルの積が定義される変な空間があってその自己同型群を使って群が構成されているが, 同じようにしてその空間を発見することが可能ではあるのだろう. 手では厳しいけど.
歴史的には分類定理のあとに八元数との関係が見いだされたはずだが, 調べていないので迂闊なことは言えない.