『正多面体と素数』の計算をしましょう(4)―正二十面体・あいだの次数・p=59問題
つづき。今回の記事からは『正多面体と素数』に書かれていないことを調べていく。
ヒルベルト-ポアンカレ級数
一つ目の記事で概説したように、ヒルベルト-ポアンカレ級数は一次独立な正二十面体多項式が各次数にいくつあるかを教えてくれる。
改めて、
\begin{align}
P(t)
= \frac{1-t^{30}}{(1-t^6)(1-t^{10})(1-t^{15})}
= \sum_{i=0}^\infty d_i t^i
\end{align}
とおこう。 が次数
の一次独立な正二十面体多項式の個数になる。最初のいくつかの項は、
\begin{align}
P(t) =& 1+{{t}^{6}}+{{t}^{10}}+{{t}^{12}}+{{t}^{15}}+{{t}^{16}}+{{t}^{18}}+{{t}^{20}}+{{t}^{21}}+{{t}^{22}}+{{t}^{24}}+{{t}^{25}}\\
&+{{t}^{26}}+{{t}^{27}}+{{t}^{28}}+2 {{t}^{30}}+{{t}^{31}}+t^{32}+t^{33}+t^{34}+t^{35}+2t^{36}+\cdots
\end{align}
であって、 がそれぞれ頂点、面、辺に対する正二十面体多項式
に対応する。
の形を見ると分かるように、
を
の
なる整数解の個数とすると、
である。これは高次の正二十面体多項式を作る方法を考えると理解できる。
の積をとると
の形で 次数
の正二十面体多項式が作られるが、
の間にはひとつの一次の関係式があるため、そのぶん独立なものが減る、ということだ。
を変形すると
は 簡単な形で表せる。
\begin{align}
P(t) =& \frac{(1+t^6+t^{12}+t^{18}+t^{24})(1+t^{10}+t^{20})(1+t^{15})}{(1-t^{30})^2}\\
=& \left(\sum_{i \in A}t^i+t^{30}\sum_{i\in B}t^i\right) \sum_{i=0}^\infty (i+1)t^{30i}\,\\
A =& \left\{0,6,10,12,15,16,18,20,21,22,24,25,26,27,28\right\},\\
B =& \left\{1,2,3,4,5,7,8,9,11,13,14,17,19,23,29\right\}
\end{align}
と、 は排反かつ和集合が0以上30未満の全ての整数になるふたつの集合
を用いて書ける。これを使うと、
\begin{align}
d_i = \left\{
\begin{aligned}
&\left\lfloor\frac{i}{30}\right\rfloor + 1, & \mbox{if } i\!\!\mod 30 \in A,\\
&\left\lfloor\frac{i}{30}\right\rfloor, & \mbox{if } i\!\!\mod 30 \in B,
\end{aligned}
\right.
\end{align}
と書ける。ただし、 は
を超えない最大の整数。OEISでは、
- A008651 - OEIS: Molien series of binary icosahedral group.
- A307897 - OEIS: Dimensions of space of harmonic polynomials of each degree invariant under the icosahedral rotation group.
が登録されている。前者は二項正二十面体群のMolien級数の係数として、後者は正二十面体対称性を持つ球面調和調和関数の重ね合わせの個数として表現されているが、これらは一致する(ひょっとすると何か違うのかと一瞬思ったが、formulaの項にあるG.f.:母関数が一致しているので間違いない)。
重複度1
の明示式を使うと、重複度(同じ次数で線型独立なものの個数)1の正二十面体多項式の次数を列挙できる。
となるような
に対して
となる整数の全体だ。
\begin{gather}
0,\,\underline{12},\,\underline{20},\,\underline{24},\,\underline{30},\,\underline{32},\,36,\,40,\,\underline{42},\,\underline{44},\,\underline{48},\,\underline{50},\,52,\,\underline{54},\,56,\\
\underline{62},\,64,\,66,\,\underline{68},\,70,\,\underline{74},\,76,\,78,\,\underline{82},\,86,\,88,\,94,\,\underline{98},\,106,\,118.
\end{gather}
ある素数 と正整数
に対して
であるような整数には下線を引いた。なお、次数0は定数。下線を引いた整数のうち、
では、中間項の係数に
が現れることを見た。それ以外の整数
ではどうなっているだろうか?
まずV-座標系で見てみよう。3つ目の記事で扱った、頂点のひとつが立体射影で無限遠点に移るような座標の取り方である。
先の3つの記事では 次の正二十面体多項式は全て同じ記号
の形で表したが、V-座標系では
、F-座標系では元のまま
、E-座標系では
で置き換えることにする。V-座標系では
\begin{align}
V_{12}(x,y) =& x^{11}y - xy^{11}+11x^{6}y^{6},\\
V_{20}(x,y) =& x^{20} + y^{20}-2^2 \!\cdot\! 3 \!\cdot\! 19\left(x^{15}y^{5} - x^{5}y^{15}\right)+2 \!\cdot\! 13 \!\cdot\! 19x^{10}y^{10},\\
V_{30}(x,y) =& x^{30} + y^{30}+2 \!\cdot\! 3^2 \!\cdot\! 29\left(x^{25}y^{5} - x^{5}y^{25}\right)-3 \!\cdot\! 5 \!\cdot\! 23 \!\cdot\! 29\left(x^{20}y^{10} + x^{10}y^{20}\right)
\end{align}
が基本となる3つの正二十面体多項式で、これらの間には
\begin{align}
1728\, V_{12}^5+V_{20}^3-V_{30}^2 = 0
\end{align}
の関係がある。
さて、これらをもとに81を除いて実際に計算してみると
\begin{align}
V_{24} =& V_{12}^2
\\=&x^{22}y^{2} + x^{2}y^{22}
\\&+2 \!\cdot\! 11\left(x^{17}y^{7} - x^{7}y^{17}\right)
\\&+7 \!\cdot\! 17\,x^{12}y^{12},\\
V_{44} =& V_{12}^2V_{20}
\\=&x^{42}y^{2} + x^{2}y^{42}
\\&-2 \!\cdot\! 103\left(x^{37}y^{7} - x^{7}y^{37}\right)
\\&-7 \!\cdot\! 17 \!\cdot\! 37\left(x^{32}y^{12} + x^{12}y^{32}\right)
\\&-2 \!\cdot\! 7 \!\cdot\! 31 \!\cdot\! 37\left(x^{27}y^{17} - x^{17}y^{27}\right)
\\&+2^2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 31 \!\cdot\! 37\,x^{22}y^{22},\\
V_{48} =& V_{12}^4
\\=&x^{44}y^{4} + x^{4}y^{44}
\\&+2^2 \!\cdot\! 11\left(x^{39}y^{9} - x^{9}y^{39}\right)
\\&+2 \!\cdot\! 19^2\left(x^{34}y^{14} + x^{14}y^{34}\right)
\\&+2^3 \!\cdot\! 11 \!\cdot\! 59\left(x^{29}y^{19} - x^{19}y^{29}\right)
\\&+5 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 29\,x^{24}y^{24},\\
V_{54} =& V_{12}^2V_{30}
\\=&x^{52}y^{2} + x^{2}y^{52}
\\&+2^5 \!\cdot\! 17\left(x^{47}y^{7} - x^{7}y^{47}\right)
\\&+2 \!\cdot\! 17 \!\cdot\! 47\left(x^{42}y^{12} + x^{12}y^{42}\right)
\\&-2 \!\cdot\! 41^2 \!\cdot\! 47\left(x^{37}y^{17} - x^{17}y^{37}\right)
\\&-17 \!\cdot\! 37 \!\cdot\! 41 \!\cdot\! 47\left(x^{32}y^{22} + x^{22}y^{32}\right),\\
V_{68} =& V_{12}^4V_{20}
\\=&x^{64}y^{4} + x^{4}y^{64}
\\&-2^3 \!\cdot\! 23\left(x^{59}y^{9} - x^{9}y^{59}\right)
\\&-2^4 \!\cdot\! 19 \!\cdot\! 29\left(x^{54}y^{14} + x^{14}y^{54}\right)
\\&-2^2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 29 \!\cdot\! 79\left(x^{49}y^{19} - x^{19}y^{49}\right)
\\&-2^3 \!\cdot\! 3^2 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 29\left(x^{44}y^{24} + x^{24}y^{44}\right)
\\&-2^4 \!\cdot\! 7 \!\cdot\! 43 \!\cdot\! 59\left(x^{39}y^{29} - x^{29}y^{39}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 7^2 \!\cdot\! 19 \!\cdot\! 37 \!\cdot\! 43\,x^{34}y^{34},\\
V_{74} =& V_{12}^2V_{20}V_{30}
\\=&x^{72}y^{2} + x^{2}y^{72}
\\&+2^2 \!\cdot\! 79\left(x^{67}y^{7} - x^{7}y^{67}\right)
\\&-2^2 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 67\left(x^{62}y^{12} + x^{12}y^{62}\right)
\\&-2 \!\cdot\! 31 \!\cdot\! 61 \!\cdot\! 67\left(x^{57}y^{17} - x^{17}y^{57}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 31 \!\cdot\! 47 \!\cdot\! 61 \!\cdot\! 67\left(x^{52}y^{22} + x^{22}y^{52}\right)
\\&+2^5 \!\cdot\! 7^2 \!\cdot\! 31 \!\cdot\! 61 \!\cdot\! 67\left(x^{47}y^{27} - x^{27}y^{47}\right)
\\&-7 \!\cdot\! 11 \!\cdot\! 43 \!\cdot\! 47 \!\cdot\! 61 \!\cdot\! 67\left(x^{42}y^{32} + x^{32}y^{42}\right),\\
V_{98} =& V_{12}^4V_{20}V_{30}
\\=&\left(x^{94}y^{4} + x^{4}y^{94}\right)
\\&+2 \!\cdot\! 13^2\left(x^{89}y^{9} - x^{9}y^{89}\right)
\\&-17 \!\cdot\! 29 \!\cdot\! 233\left(x^{84}y^{14} + x^{14}y^{84}\right)
\\&-2^2 \!\cdot\! 3 \!\cdot\! 29 \!\cdot\! 8329\left(x^{79}y^{19} - x^{19}y^{79}\right)
\\&+3 \!\cdot\! 5^2 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 29 \!\cdot\! 79\left(x^{74}y^{24} + x^{24}y^{74}\right)
\\&+2 \!\cdot\! 37 \!\cdot\! 73 \!\cdot\! 79 \!\cdot\! 2243\left(x^{69}y^{29} - x^{29}y^{69}\right)
\\&+13 \!\cdot\! 37 \!\cdot\! 43 \!\cdot\! 67 \!\cdot\! 73 \!\cdot\! 79\left(x^{64}y^{34} + x^{34}y^{64}\right)
\\&+2^3 \!\cdot\! 47 \!\cdot\! 61 \!\cdot\! 67 \!\cdot\! 73 \!\cdot\! 79\left(x^{59}y^{39} - x^{39}y^{59}\right)
\\&-2 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 61 \!\cdot\! 67 \!\cdot\! 73 \!\cdot\! 79\left(x^{54}y^{44} + x^{44}y^{54}\right)
\end{align}
という具合で、 の中間項の係数の因数には
が見当たらない。完全に回避している。これはいったいどういうことだろう。
除いた で起こることは少し興味深い。
\begin{align}
V_{82}
=& V_{12}V_{20}^2V_{30}\\
=&x^{81}y - xy^{81}
\\&+7 \!\cdot\! 11\left(x^{76}y^{6} + x^{6}y^{76}\right)
\\&-2^2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 41 \!\cdot\! 79\left(x^{71}y^{11} - x^{11}y^{71}\right)
\\&+5^2 \!\cdot\! 17 \!\cdot\! 23 \!\cdot\! 43 \!\cdot\! 71\left(x^{66}y^{16} + x^{16}y^{66}\right)
\\&-2 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 23 \!\cdot\! 31 \!\cdot\! 53 \!\cdot\! 71\left(x^{61}y^{21} - x^{21}y^{61}\right)
\\&-3 \!\cdot\! 7 \!\cdot\! 29 \!\cdot\! 31 \!\cdot\! 59 \!\cdot\! 61 \!\cdot\! 71\left(x^{56}y^{26} + x^{26}y^{56}\right)
\\&+2^2 \!\cdot\! 11 \!\cdot\! 41 \!\cdot\! 53 \!\cdot\! 59 \!\cdot\! 61 \!\cdot\! 71\left(x^{51}y^{31} - x^{31}y^{51}\right)
\\&-5 \!\cdot\! 7 \!\cdot\! 47 \!\cdot\! 53 \!\cdot\! 59 \!\cdot\! 61 \!\cdot\! 71\left(x^{46}y^{36} + x^{36}y^{46}\right)
\end{align}
中間項のうち、 の指数がともに3の倍数ではない項の係数には 3 が現れ、そうでないとき現れない。しかしE,F-座標系では同様の現象は起こらない(かなり長大な式になるのでここには載せない)ので、一般化して語るには少し苦しい。
重複度2
重複度2の場合を考える。重複度1の場合で列挙した整数に60を加えればよい。
\begin{gather}
\underline{60},\,\underline{72},\,\underline{80},\,\underline{84},\,\underline{90},\,92,\,96,\,100,\,\underline{102},\,\underline{104},\,\underline{108},\,\underline{110},\,112,\,\underline{114},\,116,\,\\
\underline{122},\,124,\,\underline{126},\,\underline{128},\,130,\,134,\,136,\,\underline{138},\,142,\,146,\,148,\,154,\,\underline{158},\,166,\,178,\,
\end{gather}
同様に素数冪 には下線を引いた。
V- 座標系
今度もV-座標系を見る。まず考えるべきは60次だろう。素数59は現れるだろうか?重複度2以上では正20面体多項式は複数存在するため、適当にラベルを付けて区別する。
\begin{align}
V_{60A} =& V_{12}^5
\\=&\,x^{55}y^{5} - x^{5}y^{55}
\\&+5 \!\cdot\! 11\left(x^{50}y^{10} + x^{10}y^{50}\right)
\\&+5 \!\cdot\! 241\left(x^{45}y^{15} - x^{15}y^{45}\right)
\\&+2 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 17\left(x^{40}y^{20} + x^{20}y^{40}\right)
\\&+3 \!\cdot\! 5 \!\cdot\! 4639\left(x^{35}y^{25} - x^{25}y^{35}\right)
\\&+11 \!\cdot\! 12251\,x^{30}y^{30},\\
V_{60B} =& V_{20}^3
\\=&\,x^{60} + y^{60}
\\&-2^2 \!\cdot\! 3^2 \!\cdot\! 19\left(x^{55}y^{5} - x^{5}y^{55}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 19 \!\cdot\! 1381\left(x^{50}y^{10} + x^{10}y^{50}\right)
\\&-2^2 \!\cdot\! 3^4 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 37\left(x^{45}y^{15} - x^{15}y^{45}\right)
\\&+3 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 737719\left(x^{40}y^{20} + x^{20}y^{40}\right)
\\&-2^3 \!\cdot\! 3^2 \!\cdot\! 19 \!\cdot\! 83 \!\cdot\! 1151\left(x^{35}y^{25} - x^{25}y^{35}\right)
\\&-2^2 \!\cdot\! 19 \!\cdot\! 436999\,x^{30}y^{30},\\
V_{60C} =& V_{30}^2
\\=&\,x^{60} + y^{60}
\\&+2^2 \!\cdot\! 3^2 \!\cdot\! 29\left(x^{55}y^{5} - x^{5}y^{55}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 29 \!\cdot\! 1451\left(x^{50}y^{10} + x^{10}y^{50}\right)
\\&-2^2 \!\cdot\! 3^3 \!\cdot\! 5 \!\cdot\! 23 \!\cdot\! 29^2\left(x^{45}y^{15} - x^{15}y^{45}\right)
\\&+3 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 23 \!\cdot\! 29 \!\cdot\! 1429\left(x^{40}y^{20} + x^{20}y^{40}\right)
\\&-2^3 \!\cdot\! 3^2 \!\cdot\! 29 \!\cdot\! 5003\left(x^{35}y^{25} - x^{25}y^{35}\right)
\\&+2^2 \!\cdot\! 5323 \!\cdot\! 9377\,x^{30}y^{30}
\end{align}
ここに59はなし。この3つに の一次の関係があることは既に述べたとおり。ところで、
は
の最高次の係数が55で、
は60である。後者に前者の定数倍を加えることで、最高次の係数を1にしたまま55次の項を消す方法がただひとつだけ存在する。それが以下の
だ;
\begin{align}
V_{60I}
=& V_{60B} + 2^2\cdot 3^2\cdot 19\, V_{60A}\\
=& V_{60C} - 2^2\cdot 3^2\cdot 29\, V_{60B}
\\=&x^{60} + y^{60}
\\&+2 \!\cdot\! 3 \!\cdot\! 19 \!\cdot\! 29 \!\cdot\! 59\left(x^{50}y^{10} + x^{10}y^{50}\right)
\\&-2^3 \!\cdot\! 3^2 \!\cdot\! 5 \!\cdot\! 19 \!\cdot\! 29 \!\cdot\! 59\left(x^{45}y^{15} - x^{15}y^{45}\right)
\\&+3 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 29 \!\cdot\! 37 \!\cdot\! 59\left(x^{40}y^{20} + x^{20}y^{40}\right)
\\&-2^2 \!\cdot\! 3^2 \!\cdot\! 19 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 71\left(x^{35}y^{25} - x^{25}y^{35}\right)
\\&+2^3 \!\cdot\! 5^2 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 263\,x^{30}y^{30}
\end{align}
何ということだろう。中間項の係数に59が現れたではないか。
ちなみにこの構成法には、アイゼンシュタイン級数を組み合わせてリーチ格子のテータ関数を得る方法を思わせるところがある。詳細は以下の記事を参照。正20面体多項式の係数にも組合せ論的な解釈がありうるのだろうか?
shironetsu.hatenadiary.com
同様に、 次ではそれぞれ中間項の係数に素数
が現れる。
\begin{align}
V_{72I}
=&V_{12}\left(673\,V_{12}^5+V_{20}^3\right)
\\=&x^{71}y - xy^{71}
\\&+7 \!\cdot\! 17 \!\cdot\! 23 \!\cdot\! 71\left(x^{61}y^{11} - x^{11}y^{61}\right)
\\&-3 \!\cdot\! 5 \!\cdot\! 17 \!\cdot\! 23^2 \!\cdot\! 71\left(x^{56}y^{16} + x^{16}y^{56}\right)
\\&-11 \!\cdot\! 23 \!\cdot\! 71 \!\cdot\! 2383\left(x^{51}y^{21} - x^{21}y^{51}\right)
\\&+3^2 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 17 \!\cdot\! 71 \!\cdot\! 887\left(x^{46}y^{26} + x^{26}y^{46}\right)
\\&-5 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 17 \!\cdot\! 23 \!\cdot\! 71 \!\cdot\! 89\left(x^{41}y^{31} - x^{31}y^{41}\right)
\\&+3 \!\cdot\! 7 \!\cdot\! 23 \!\cdot\! 41 \!\cdot\! 71 \!\cdot\! 569\,x^{36}y^{36},\\
V_{80I} =& V_{20}\left(2^4\cdot 3\cdot 19 V_{12}^5+V_{20}^3\right)
\\=&x^{80} + y^{80}
\\&+2^3 \!\cdot\! 13 \!\cdot\! 19 \!\cdot\! 79\left(x^{70}y^{10} + x^{10}y^{70}\right)
\\&-2^5 \!\cdot\! 3 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 37 \!\cdot\! 79\left(x^{65}y^{15} - x^{15}y^{65}\right)
\\&+2^2 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 17 \!\cdot\! 59 \!\cdot\! 79 \!\cdot\! 97\left(x^{60}y^{20} + x^{20}y^{60}\right)
\\&-2^4 \!\cdot\! 3 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 19 \!\cdot\! 29 \!\cdot\! 79 \!\cdot\! 137\left(x^{55}y^{25} - x^{25}y^{55}\right)
\\&+2^3 \!\cdot\! 13 \!\cdot\! 19 \!\cdot\! 79 \!\cdot\! 179 \!\cdot\! 2039\left(x^{50}y^{30} + x^{30}y^{50}\right)
\\&-2^4 \!\cdot\! 3^3 \!\cdot\! 7 \!\cdot\! 13 \!\cdot\! 19 \!\cdot\! 79 \!\cdot\! 563\left(x^{45}y^{35} - x^{35}y^{45}\right)
\\&+2 \!\cdot\! 7^2 \!\cdot\! 43 \!\cdot\! 79 \!\cdot\! 41543\,x^{40}y^{40},\\
V_{90I} =& V_{30}\left(-2\cdot 3^3\cdot 29V_{12}^5+V_{30}^2\right)
\\=&x^{90} + y^{90}
\\&-3^2 \!\cdot\! 5 \!\cdot\! 29 \!\cdot\! 89\left(x^{80}y^{10} + x^{10}y^{80}\right)
\\&+2^3 \!\cdot\! 3^3 \!\cdot\! 11 \!\cdot\! 13 \!\cdot\! 29 \!\cdot\! 89\left(x^{75}y^{15} - x^{15}y^{75}\right)
\\&-2 \!\cdot\! 3^2 \!\cdot\! 5^2 \!\cdot\! 29 \!\cdot\! 89 \!\cdot\! 6907\left(x^{70}y^{20} + x^{20}y^{70}\right)
\\&+2 \!\cdot\! 3^3 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 89 \!\cdot\! 193 \!\cdot\! 557\left(x^{65}y^{25} - x^{25}y^{65}\right)
\\&-2^4 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 89 \!\cdot\! 40272443\left(x^{60}y^{30} + x^{30}y^{60}\right)
\\&+2^3 \!\cdot\! 3^3 \!\cdot\! 5 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 79 \!\cdot\! 89 \!\cdot\! 101\left(x^{55}y^{35} - x^{35}y^{55}\right)
\\&-2 \!\cdot\! 3^2 \!\cdot\! 29 \!\cdot\! 41 \!\cdot\! 53 \!\cdot\! 59 \!\cdot\! 89 \!\cdot\! 103\left(x^{50}y^{40} + x^{40}y^{50}\right),\\
V_{102I} =& V_{12}V_{30}\left(-19\cdot 83\,V_{12}^5+V_{30}^2\right)
\\=&x^{101}y - xy^{101}
\\&-2 \!\cdot\! 101 \!\cdot\! 607\left(x^{91}y^{11} - x^{11}y^{91}\right)
\\&+3 \!\cdot\! 11 \!\cdot\! 101 \!\cdot\! 131 \!\cdot\! 179\left(x^{86}y^{16} + x^{16}y^{86}\right)
\\&-5 \!\cdot\! 11^2 \!\cdot\! 13 \!\cdot\! 101 \!\cdot\! 8999\left(x^{81}y^{21} - x^{21}y^{81}\right)
\\&+2^2 \!\cdot\! 3^3 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 101 \!\cdot\! 91121\left(x^{76}y^{26} + x^{26}y^{76}\right)
\\&+2^2 \!\cdot\! 3^2 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 61 \!\cdot\! 101 \!\cdot\! 78893\left(x^{71}y^{31} - x^{31}y^{71}\right)
\\&-3 \!\cdot\! 71 \!\cdot\! 101 \!\cdot\! 385651667\left(x^{66}y^{36} + x^{36}y^{66}\right)
\\&+2 \!\cdot\! 3^2 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 71 \!\cdot\! 101 \!\cdot\! 353 \!\cdot\! 4211\left(x^{61}y^{41} - x^{41}y^{61}\right)
\\&-2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 17 \!\cdot\! 59 \!\cdot\! 61 \!\cdot\! 71 \!\cdot\! 101 \!\cdot\! 599\left(x^{56}y^{46} + x^{46}y^{56}\right),\\
V_{110I} =& V_{20}V_{30}\left(-2\cdot 3\cdot 223\,V_{12}^5+V_{30}^2\right)
\\=&x^{110} + y^{110}
\\&-109 \!\cdot\! 331\left(x^{100}y^{10} + x^{10}y^{100}\right)
\\&+2^4 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 109 \!\cdot\! 281\left(x^{95}y^{15} - x^{15}y^{95}\right)
\\&-5 \!\cdot\! 7 \!\cdot\! 53 \!\cdot\! 109 \!\cdot\! 157 \!\cdot\! 857\left(x^{90}y^{20} + x^{20}y^{90}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 47 \!\cdot\! 109 \!\cdot\! 263 \!\cdot\! 787\left(x^{85}y^{25} - x^{25}y^{85}\right)
\\&-3 \!\cdot\! 5^3 \!\cdot\! 109 \!\cdot\! 337 \!\cdot\! 1019 \!\cdot\! 3001\left(x^{80}y^{30} + x^{30}y^{80}\right)
\\&+2^2 \!\cdot\! 3^2 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 79 \!\cdot\! 109 \!\cdot\! 4340993\left(x^{75}y^{35} - x^{35}y^{75}\right)
\\&-2^2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 7^2 \!\cdot\! 73 \!\cdot\! 79 \!\cdot\! 109 \!\cdot\! 173 \!\cdot\! 2081\left(x^{70}y^{40} + x^{40}y^{70}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 67 \!\cdot\! 73 \!\cdot\! 79 \!\cdot\! 109 \!\cdot\! 42751\left(x^{65}y^{45} - x^{45}y^{65}\right)
\\&-2 \!\cdot\! 3 \!\cdot\! 7 \!\cdot\! 29 \!\cdot\! 61 \!\cdot\! 67^2 \!\cdot\! 73 \!\cdot\! 79 \!\cdot\! 109\left(x^{60}y^{50} + x^{50}y^{60}\right)
\end{align}
の場合には
と似たことが起こり、中間項のうち
の指数が11の倍数である場合には係数は11で、そうでない場合は
で割り切れる。
\begin{align}
V_{122I} =& V_{12}V_{20}V_{30}\left(379V_{12}^5+V_{20}^3\right)
\\=&x^{121}y - xy^{121}
\\&-2^3 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 13\left(x^{111}y^{11} - x^{11}y^{111}\right)
\\&+3 \!\cdot\! 5 \!\cdot\! 11^2 \!\cdot\! 44983\left(x^{106}y^{16} + x^{16}y^{106}\right)
\\&-2 \!\cdot\! 3^2 \!\cdot\! 11^2 \!\cdot\! 13^2 \!\cdot\! 71333\left(x^{101}y^{21} - x^{21}y^{101}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 7 \!\cdot\! 11^3 \!\cdot\! 73 \!\cdot\! 424147\left(x^{96}y^{26} + x^{26}y^{96}\right)
\\&-2^6 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 11^3 \!\cdot\! 233 \!\cdot\! 28477\left(x^{91}y^{31} - x^{31}y^{91}\right)
\\&-2 \!\cdot\! 3^2 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 11^3 \!\cdot\! 13 \!\cdot\! 113 \!\cdot\! 149767\left(x^{86}y^{36} + x^{36}y^{86}\right)
\\&+5 \!\cdot\! 7 \!\cdot\! 11^3 \!\cdot\! 43 \!\cdot\! 631 \!\cdot\! 1951951\left(x^{81}y^{41} - x^{41}y^{81}\right)
\\&-2^3 \!\cdot\! 3^2 \!\cdot\! 7 \!\cdot\! 11^2 \!\cdot\! 13 \!\cdot\! 79 \!\cdot\! 8161 \!\cdot\! 13729\left(x^{76}y^{46} + x^{46}y^{76}\right)
\\&+2^2 \!\cdot\! 3^2 \!\cdot\! 11^2 \!\cdot\! 13 \!\cdot\! 73 \!\cdot\! 79 \!\cdot\! 1627 \!\cdot\! 13177\left(x^{71}y^{51} - x^{51}y^{71}\right)
\\&-3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 61 \!\cdot\! 67 \!\cdot\! 71 \!\cdot\! 73 \!\cdot\! 79 \!\cdot\! 10111\left(x^{66}y^{56} + x^{56}y^{66}\right)
\end{align}
一方、 では同じことは起こらない。たとえば84次では
\begin{align}
V_{84I}(x,y) =& V_{12}^2\left(2\cdot 331\,V_{12}^5+V_{20}^3\right)
\\=&x^{82}y^{2} + x^{2}y^{82}
\\&+3 \!\cdot\! 11^2 \!\cdot\! 13 \!\cdot\! 41\left(x^{72}y^{12} + x^{12}y^{72}\right)
\\&-2 \!\cdot\! 3^3 \!\cdot\! 41 \!\cdot\! 3373\left(x^{67}y^{17} - x^{17}y^{67}\right)
\\&-2^3 \!\cdot\! 3^4 \!\cdot\! 13 \!\cdot\! 41 \!\cdot\! 431\left(x^{62}y^{22} + x^{22}y^{62}\right)
\\&+2^3 \!\cdot\! 7^2 \!\cdot\! 31 \!\cdot\! 41 \!\cdot\! 823\left(x^{57}y^{27} - x^{27}y^{57}\right)
\\&+3^3 \!\cdot\! 11 \!\cdot\! 23 \!\cdot\! 41 \!\cdot\! 31069\left(x^{52}y^{32} + x^{32}y^{52}\right)
\\&-2^3 \!\cdot\! 3^2 \!\cdot\! 7^2 \!\cdot\! 13 \!\cdot\! 41 \!\cdot\! 5669\left(x^{47}y^{37} - x^{37}y^{47}\right)
\\&+2^2 \!\cdot\! 3^2 \!\cdot\! 11 \!\cdot\! 13 \!\cdot\! 19 \!\cdot\! 47 \!\cdot\! 2297\,x^{42}y^{42}
\end{align}
となっている。素数83は見当たらない。
ただ は少し特殊で、中間項の係数には 5 が現れたり現れなかったりする。
\begin{align}
V_{126I} =& V_{12}^3V_{30}\left(-3\cdot 13\cdot 41 V_{12}^5+V_{30}^2\right)
\\=&x^{123}y^{3} - x^{3}y^{123}
\\&-3 \!\cdot\! 5 \!\cdot\! 13 \!\cdot\! 17 \!\cdot\! 41\left(x^{113}y^{13} - x^{13}y^{113}\right)
\\&+5 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 41 \!\cdot\! 1741\left(x^{108}y^{18} + x^{18}y^{108}\right)
\\&-2 \!\cdot\! 3^2 \!\cdot\! 13 \!\cdot\! 41 \!\cdot\! 569599\left(x^{103}y^{23} - x^{23}y^{103}\right)
\\&-3 \!\cdot\! 11 \!\cdot\! 17 \!\cdot\! 41 \!\cdot\! 3111013\left(x^{98}y^{28} + x^{28}y^{98}\right)
\\&+5 \!\cdot\! 17 \!\cdot\! 41 \!\cdot\! 97 \!\cdot\! 2087 \!\cdot\! 2549\left(x^{93}y^{33} - x^{33}y^{93}\right)
\\&+2 \!\cdot\! 3 \!\cdot\! 5 \!\cdot\! 13 \!\cdot\! 41 \!\cdot\! 67 \!\cdot\! 97 \!\cdot\! 283 \!\cdot\! 757\left(x^{88}y^{38} + x^{38}y^{88}\right)
\\&-3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 17 \!\cdot\! 97 \!\cdot\! 13879 \!\cdot\! 14173\left(x^{83}y^{43} - x^{43}y^{83}\right)
\\&-3 \!\cdot\! 17 \!\cdot\! 41 \!\cdot\! 83 \!\cdot\! 97 \!\cdot\! 40540037\left(x^{78}y^{48} + x^{48}y^{78}\right)
\\&+2^2 \!\cdot\! 3^2 \!\cdot\! 11 \!\cdot\! 41 \!\cdot\! 83 \!\cdot\! 97 \!\cdot\! 13748939\left(x^{73}y^{53} - x^{53}y^{73}\right)
\\&-3^2 \!\cdot\! 5 \!\cdot\! 7^3 \!\cdot\! 41 \!\cdot\! 47 \!\cdot\! 71 \!\cdot\! 73 \!\cdot\! 83 \!\cdot\! 97\left(x^{68}y^{58} + x^{58}y^{68}\right)
\end{align}
ところで、もし法5で である素数冪でこのような現象が引き続き起こる(と予想するには尚早だが)なら、逆に起こらないのは
に限られる。
は6次交代群と同型という極めて例外的な性質を持つ。
F-座標系
F-座標系(二つ目の記事を参照)では60次の場合だけ見る。基本となる正二十面体多項式3つは、
\begin{align}
F_{12}
=&x^{12} + y^{12}
\\&+11\sqrt{5}\left(x^{9}y^{3} - x^{3}y^{9}\right)
\\&-3 \!\cdot\! 11\,x^{6}y^{6},\\
F_{20}
=&x^{19}y - xy^{19}
\\&-\frac{3 \!\cdot\! 19\sqrt{5}}{2^3}\left(x^{16}y^{4} + x^{4}y^{16}\right)
\\&-\frac{3 \!\cdot\! 19}{2}\left(x^{13}y^{7} - x^{7}y^{13}\right)
\\&-\frac{13 \!\cdot\! 19\sqrt{5}}{2^2}\,x^{10}y^{10},\\
F_{30}
=&x^{30} + y^{30}
\\&-\frac{5 \!\cdot\! 29\sqrt{5}}{2}\left(x^{27}y^{3} - x^{3}y^{27}\right)
\\&+\frac{3^3 \!\cdot\! 5 \!\cdot\! 29}{2^3}\left(x^{24}y^{6} + x^{6}y^{24}\right)
\\&-\frac{3 \!\cdot\! 5 \!\cdot\! 23 \!\cdot\! 29\sqrt{5}}{2^2}\left(x^{21}y^{9} - x^{9}y^{21}\right)
\\&-\frac{3 \!\cdot\! 5 \!\cdot\! 19 \!\cdot\! 23 \!\cdot\! 29}{2^3}\left(x^{18}y^{12} + x^{12}y^{18}\right)
\end{align}
であって、これらの間には
\begin{align}
F_{12}^5-200\sqrt{5}\,F_{20}^3-F_{30}^2 =0
\end{align}
の関係がある。V-座標系の場合と同様に、最高次から2番目の次数の係数が消えるようにすると、
\begin{align}
F_{60I}
=& F_{12}^5 - 5\cdot 11\sqrt{5}\, F_{20}^3\\
=& F_{30}^2 + 5 \cdot 29\sqrt{5}\, F_{20}^3\\
=&+\left(x^{60} + y^{60}\right)
\\&+\frac{5 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 59}{2^3}\left(x^{54}y^{6} + x^{6}y^{54}\right)
\\&+\frac{3 \!\cdot\! 5^2 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 59\sqrt{5}}{2^6}\left(x^{51}y^{9} - x^{9}y^{51}\right)
\\&+\frac{3^3 \!\cdot\! 5 \!\cdot\! 7 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 457}{2^9}\left(x^{48}y^{12} + x^{12}y^{48}\right)
\\&+\frac{3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 59^2\sqrt{5}}{2^7}\left(x^{45}y^{15} - x^{15}y^{45}\right)
\\&-\frac{3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 83 \!\cdot\! 349}{2^8}\left(x^{42}y^{18} + x^{18}y^{42}\right)
\\&+\frac{3^3 \!\cdot\! 5 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 3797\sqrt{5}}{2^7}\left(x^{39}y^{21} - x^{21}y^{39}\right)
\\&+\frac{3 \!\cdot\! 5 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 1231 \!\cdot\! 2423}{2^9}\left(x^{36}y^{24} + x^{24}y^{36}\right)
\\&-\frac{5 \!\cdot\! 7^2 \!\cdot\! 11 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 379\sqrt{5}}{2^5}\left(x^{33}y^{27} - x^{27}y^{33}\right)
\\&+\frac{3^4 \!\cdot\! 11 \!\cdot\! 59 \!\cdot\! 820349}{2^7}\,x^{30}y^{30}
\end{align}
を得る。今度も中間項の係数には59が現れた。
E-座標系
E-座標系(最初の記事を参照)では、基本の正二十面体多項式3つは
\begin{align}
E_{12} =& x^{12} + y^{12}
\\&-\frac{2 \!\cdot\! 11}{\sqrt{5}}\left(x^{10}y^{2} + x^{2}y^{10}\right)
\\&-3 \!\cdot\! 11\left(x^{8}y^{4} + x^{4}y^{8}\right)
\\&+\frac{2^2 \!\cdot\! 11}{\sqrt{5}}\,x^{6}y^{6},\\
E_{20} =& x^{20} + y^{20}
\\&+\frac{2 \!\cdot\! 19\sqrt{5}}{3}\left(x^{18}y^{2} + x^{2}y^{18}\right)
\\&-19\left(x^{16}y^{4} + x^{4}y^{16}\right)
\\&+2^3 \!\cdot\! 19\sqrt{5}\left(x^{14}y^{6} + x^{6}y^{14}\right)
\\&-2 \!\cdot\! 13 \!\cdot\! 19\left(x^{12}y^{8} + x^{8}y^{12}\right)
\\&-\frac{2^2 \!\cdot\! 13 \!\cdot\! 19\sqrt{5}}{3}\,x^{10}y^{10},\\
E_{30} =& x^{29}y - xy^{29}
\\&+\frac{2^2 \!\cdot\! 29}{3^2\sqrt{5}}\left(x^{27}y^{3} - x^{3}y^{27}\right)
\\&+\frac{29 \!\cdot\! 61}{5^2}\left(x^{25}y^{5} - x^{5}y^{25}\right)
\\&-\frac{2^4 \!\cdot\! 29}{\sqrt{5}}\left(x^{23}y^{7} - x^{7}y^{23}\right)
\\&+\frac{3 \!\cdot\! 23 \!\cdot\! 29}{5}\left(x^{21}y^{9} - x^{9}y^{21}\right)
\\&+\frac{2^2 \!\cdot\! 23 \!\cdot\! 29}{3\sqrt{5}}\left(x^{19}y^{11} - x^{11}y^{19}\right)
\\&+\frac{19 \!\cdot\! 23 \!\cdot\! 29}{5}\left(x^{17}y^{13} - x^{13}y^{17}\right)
\end{align}
で、これらの間には
\begin{align}
E_{12}^5-E_{20}^3+60\sqrt{5}\,E_{30}^2 = 0
\end{align}
の関係がある。同様に、60次の正二十面体多項式として
\begin{align}
E_{60I} =& E_{12}^5+2\cdot 11\,\sqrt{5}\,E_{30}^2
\\=& E_{20}^3-2\cdot 19\,\sqrt{5}\,E_{30}^2
\\=&x^{60} + y^{60}
\\&+\frac{11 \!\cdot\! 19 \!\cdot\! 59}{3^2}\left(x^{56}y^{4} + x^{4}y^{56}\right)
\\&+\frac{2^5 \!\cdot\! 11 \!\cdot\! 13 \!\cdot\! 19 \!\cdot\! 59}{3^4 \!\cdot\! 5\sqrt{5}}\left(x^{54}y^{6} + x^{6}y^{54}\right)
\\&-\frac{11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 409}{3^2 \!\cdot\! 5^2}\left(x^{52}y^{8} + x^{8}y^{52}\right)
\\&+\frac{2^7 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 691}{3^2 \!\cdot\! 5^3\sqrt{5}}\left(x^{50}y^{10} + x^{10}y^{50}\right)
\\&+\frac{7 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 179}{3 \!\cdot\! 5^2}\left(x^{48}y^{12} + x^{12}y^{48}\right)
\\&-\frac{2^6 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 557}{3^3 \!\cdot\! 5^2\sqrt{5}}\left(x^{46}y^{14} + x^{14}y^{46}\right)
\\&-\frac{11 \!\cdot\! 19 \!\cdot\! 29 \!\cdot\! 59 \!\cdot\! 17789}{3^2 \!\cdot\! 5^2}\left(x^{44}y^{16} + x^{16}y^{44}\right)
\\&+\frac{2^7 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 1033}{3 \!\cdot\! 5^2\sqrt{5}}\left(x^{42}y^{18} + x^{18}y^{42}\right)
\\&-\frac{7 \!\cdot\! 11 \!\cdot\! 59 \!\cdot\! 557611}{3^2 \!\cdot\! 5}\left(x^{40}y^{20} + x^{20}y^{40}\right)
\\&-\frac{2^5 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 286043}{3^3 \!\cdot\! 5^2\sqrt{5}}\left(x^{38}y^{22} + x^{22}y^{38}\right)
\\&+\frac{7 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 967 \!\cdot\! 1523}{3 \!\cdot\! 5^2}\left(x^{36}y^{24} + x^{24}y^{36}\right)
\\&+\frac{2^8 \!\cdot\! 7 \!\cdot\! 11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 4673}{3^2 \!\cdot\! 5^2\sqrt{5}}\left(x^{34}y^{26} + x^{26}y^{34}\right)
\\&-\frac{11 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 737641}{3 \!\cdot\! 5}\left(x^{32}y^{28} + x^{28}y^{32}\right)
\\&-\frac{2^7 \!\cdot\! 11^2 \!\cdot\! 19 \!\cdot\! 59 \!\cdot\! 365983}{3^4 \!\cdot\! 5^3\sqrt{5}}\,x^{30}y^{30}
\end{align}
を得て、やはり中間項の係数には59が現れる。
今回の観察結果の何が喜ばしいかというと、正多面体と素数の関わりが有限個で閉じたものではない可能性が出てきたことだ。重複度3以上の場合はどうなるだろうか?既に数式処理ソフト頼りとはいえ、対話式で計算していくには少々厳しくなってきたので、準備をしてから取り組みたい。
球面調和関数
60次の場合を球面調和関数として見ておく。
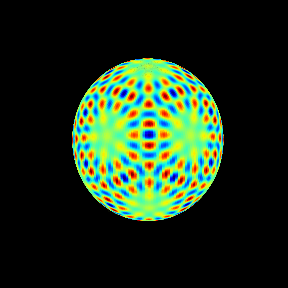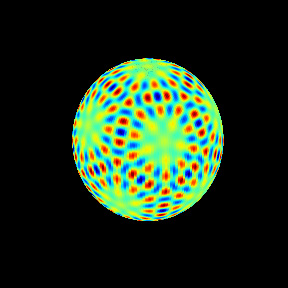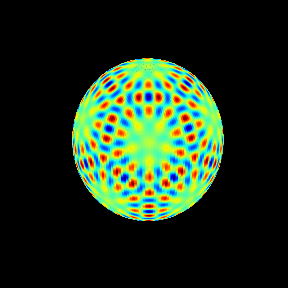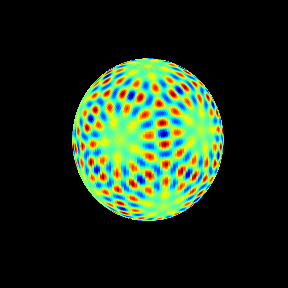
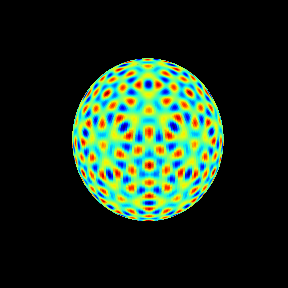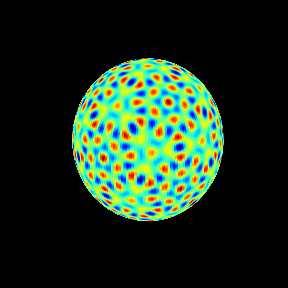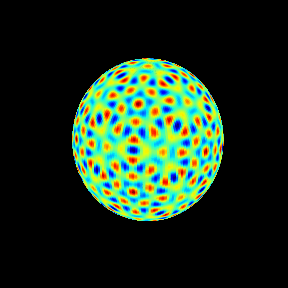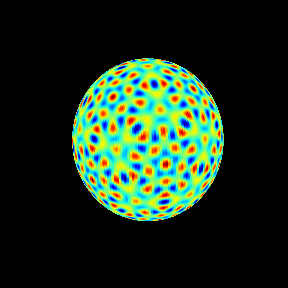

今回はここまで。次は重複度3以上の場合、 の根(リーマン球面上の基本領域にひとつ存在する)などを調べてゆきたい。
計算ノートは以下のリポジトリに順次追加予定です。