このマグロがすごい！2023─『マグロちゃんは食べられたい！』最新話の何がすごいか

釣り上げたマグロが少女に変わる。元マグロ少女と生活を共にすることになる。価値観の違いに振り回されつつコメディが進行する。やがて第二、第三の元マグロ少女が現れ更に主人公の周囲を賑やかにする。

やや色物の、「素朴に」とか「しみじみと」といったタイプの面白さのある漫画に見えて、実際それもそうなのだけれど、連載最新話で急激に「芯」のある面白さを感じはじめたので紹介したい。

髪が赤いのがみさき（釣り主、人間）で、髪が白いのがまぐろちゃん（釣り上げられた元マグロ）

漫画の連載を雑誌で追っていると、それまでしっかり向き合っていなかった漫画の面白さを再発見する回というものにしばしば遭遇する。部屋の隅に積んであるバックナンバーを遡る。単行本を頭から読み通す。読んだことのある回の、あの描写この台詞の深みに気付く。

『マグロちゃんは食べられたい！』最新話がそうだった。

◤きららMAX4月号の大人気連載◢

『マグロちゃんは食べられたい！』では、
みさきの両親から大荷物が届いた模様🐟
どうやらまぐろちゃんとの関係♥を
思いっきり勘違いされてるみたいですね♥

【無料マグロ、あり🐟】https://t.co/YRyOVwDmJC pic.twitter.com/SGIwPXNbbm
— まんがタイムきらら編集部 (@mangatimekirara) February 16, 2023

みさきさんと同じ服を着て
同じ布団で眠って
同じ暮らしをして

それだけでこんなに満たされた気持ちになるなら
本当の意味でいっしょになったらどんなに幸せなんでしょうか

このしっとりとした語りが、いかにもカラッとして朗らかな元マグロ少女まぐろちゃんの心の内でつぶやかれる。

この台詞はすごい。ここまで積み上げてきたエピソードたちがこのモノローグに文字面だけでない意味を与えて、逆にこの台詞がこれまでのエピソードの細部の造型に気付かせてくれる。

どうすごいか。

すごさ1. お揃いのパジャマを着るというプチイベントからこの台詞が発生する。

前提として、「本当の意味でいっしょになったら」はこのまぐろちゃん（元マグロ）がみさき（生まれつき人間）に食べられることを言う。この作品ではみさきの「血肉になりたい」という言葉がまぐろちゃんから繰り返し発せられる。 自分を釣り上げた人間に食べられて血肉を捧げる、というのが「マグロの掟」で、まぐろちゃんはどこまでもそれに従おうとする。

そこへある日サイズも色も同じ2セットのひらひらのパジャマが届く。洗濯するとどっちがどっちか分からない、という現実的な心配をみさきがする一方、まぐろちゃんはみさきと向かい合い両手のひらを合わせて、

こうすると鏡を見ているみたいです

今はまだみさきさんに食べて頂けませんけど…

これを着ていると一緒になれたみたいで嬉しいです

と、感じたことを無邪気に率直に伝える。

で、その晩の台詞が「本当の意味でいっしょになったらどんなに幸せなんでしょうか」で、いっしょのパジャマを着ていっしょに生活するだけでこんなに幸せなら、本当の意味でいっしょになる=食べられて血肉になればもっと幸せだろう、という全く人間とは異質なロジックが展開されている。すごい。まぐろちゃんという生き物の感性を丁寧にトレースすること生まれた表現。

これを実は結構怖いことを言っていることに気付かせないくらいの、ごく明るい調子で発する。それが味わい深い。

すごさ2. 一方でそのすぐ後の「アンタは家族みたいなもんよ」というみさきの言葉を全く受け入れない。

人間としてはこれほど愛のこもった台詞はない。が、まぐろちゃんは「そんなの嫌です！」と即応する。なぜ？（ウミガメのスープ）

家族みたいに受け入れてくれることは元マグロにとって幸福のひとつの形ですらない。なぜならマグロは血縁で群れを作らないから。いつか自分のことを食べてほしいのに、「家族」なんかに思われるのは嫌なのだ。

なお、定番ギャグのひとつである「共食い」をこの漫画でもやっている。マグロの寿司は「昔食べた兄弟の味を思い出」すらしい（筆者がいちばんすきなコマのひとつ……）。元マグロにとって、血縁は愛や幸福と全く結びつかない。

すごさ3. みさきはまぐろに対して、食べられたいという願いを忘れてしまうよう本心から迫っている。

遡って2022年12月号の掲載回にあるみさきの台詞。

人間の世界にはまだまだ美味しいものがたくさんあるわ
魚だけじゃないしたのしいこともいっぱいあるの
だからさ…

やめちゃわない？
私に食べられるの

みさきさん私を食べてください！→食べないから！という、コメディ調の掛け合いがお決まりの流れになっているところに、意を決したみさきが放った言葉。文字だけ書き起こすと改めて感じる。重い……。

この改まった提案をまぐろちゃんは断る。

確かにみさきさんと一緒にいるのは楽しいです
でも
食べて頂けない限り　いつか必ずお別れが来るじゃないですか

（中略）

私は貴方に食べられたいんです
みさきさんにとって私が運命の魚じゃなくても
私の運命の人はみさきさんだけですから

このやりとりはここで終わる。終わるが、みさきはここであきらめたわけではなく、「あの子自身の気持ちを私が見つけて見せるわ」と意を新たにする。

そこへ「本当の意味でいっしょになったらどんなに幸せなんでしょうか」が投じられる。みさきの決意をよそに、まぐろちゃんは普通の人間として生きる喜びに気付くどころか、食べられて一緒になることへの願望をより一層募らせていた。まぐろちゃん自身の気持ちは今のところ全く「みさきと一緒に過ごすこと」に向かっていない。むしろ、ただ「釣り上げられた人間に食べられる」という掟に「縛られる」段階を脱していて、そのなかに自分自身で新たに意味を発見している。

また別の回（きららMAX2023/02号）でまぐろちゃんはこうも言う。

みさきさんが私を食べたくないなら
食べずにはいられないような至高のマグロを目指さなきゃ

まぐろちゃんもまた、みさきが心変わりすることを望んでいる。一緒に日々を過ごすのではなくて、自分を食べたくなるように。

みさきはまぐろちゃんのことを突然できた妹のような存在に感じている。ただ一緒に暮らすことに既に幸せを見出している。対して、まぐろちゃんは自分を釣り上げたみさきに対して崇拝めいた感情で向き合って、こうして早く食べられることを願っている。

お互いに相手の幸せのあり方が塗り替わることを求める。どちらもそれぞれ相手のことを慮りつつも利己的で、お互いが目指す幸福の形を認めていない。

膠着状態。「私の幸せと貴方の幸せが両立しない」って……「綺麗」だ……。

すごさ4. 「一緒になるのと一緒にいるのは全然別のことだ」という台詞がもっと前の回に出ている。

アンサーか？と思うところだが、これが出てきたのはもっと前の第5話（最新話が15話だから、10回前）。同じく元マグロ少女（正確にはバショウカジキ）のカジキちゃんから発せられたもの。すごい、本質的な台詞がずっと前に出ていた。

そう、まぐろちゃんは一緒になるのと一緒にいることを同一視している。この指摘は一顧だにされないまま今に至るわけだが、まぐろちゃんが気付くかもしれないし気付かないかもしれないテーマは既に提示されていたことになる。

ところでカジキちゃんもまたみさきの幼馴染なぎさ（生まれつき人間）と生活を共にすることになる。この2人はみさき＆まぐろと逆に、元魚のカジキの方がずっと一緒でいることを望んでいて、対照的な関係になっている。そのことを認識するとまた見え方が変わってきて……というのは割愛。

こうして読み返すと新たに発見があるもので、この「マグロちゃんは食べられたい！」という漫画は、「食べられたい！」という願望を色々な角度から眺めて、それとない風に真剣かつ丁寧に扱っている。それを日常コメディの中に織り交ぜるのが非常にうまい。

紹介と言いつつ連載最新話までめちゃめちゃネタバレした（自己弁護するとこれくらいのネタバレで読む楽しみが減じるような漫画じゃない。結局のところ、文字で伝わる4コマ漫画の魅力というものは一側面に過ぎない）。みさきとまぐろの行く先がどうなるのか、連載を読んで、今一番ライブで追ってほしい漫画です。

【無料マグロ、あり🐟】

seiga.nicovideo.jp

www.dokidokivisual.com

2023-01-22

ベジェルとウル・コーマは北京五輪で何番目に入場するか？

ベジェルとウル・コーマ
北京オリンピックの開会式
笔顺编号
漢字と近代文明
ソートプログラム
贝歇尓と乌库姆
リファレンス

ベジェルとウル・コーマ

厚かましく自信たっぷりなベジェルとウル・コーマの検閲体制が寛容なのか、それとも無能なのか、リンク先のアドレスに ".uq" ".zb" がついているものがたくさんあった

チャイナ・ミエヴィル『都市と都市』（早川書房）p.156

架空の国家の……トップレベルドメイン……！！　「ベジェル」（Besźel）が".zb"[1]で、「ウル・コーマ」（Ul Qoma）が".uq"。日本なら".jp"とつくあれです。

[1] ちなみにベジェルが".bz"や".be"でないのは、それぞれベリーズやベルギーの実在のドメインと被るため。

ベジェル企業は ".zb" ドメインにホームページを開設し、ウル・コーマの人々は "Amazon.co.uq" で買い物を楽しむ。たったこれだけの設定とはいえ、現代を生きる両国民の息遣いが感じられないでしょうか。

小説『都市と都市』には、2つの架空の都市国家「ベジェル」（Besźel）と「ウル・コーマ」（Ul Qoma）のリアリティを高めるための設定がこの他にもたくさん詰め込まれています。

www.hayakawa-online.co.jp

極め付けは5章の冒頭。ベジェルで使われる「ベジェル語」とウル・コーマの「イリット語」に関して、

ベジェル語のベジェル文字は三十四字からなるアルファベットで、左から右に書き、キリル文字に見た目が似る。
イリット語はかつて右から左へ書く固有の文字を有していたが、1923年の「ヤー・イルサ改革」でラテンアルファベットに置き換えられた。
ヤー・イルサ改革は、アタテュルクによるトルコ語の言語改革に影響を与えている。公式の表記をアラビア文字からラテン文字に置き換えたもの。

という「歴史的事実」が簡潔に説明されます。現実との絡め方が絶妙で、ここで読者は「設定を鑑賞すること」の歓喜に打ち震えることでしょう。言語は国家の基礎をなすもの。設定面からもこの2つの国家に強度が与えられ、一層のリアリティを帯びて迫ってきます。

さて、『都市と都市』を読み終えると、この類の空想を楽しむ余地がまだまだ残されていることに気付きます。つまり、ベジェルとウル・コーマに関する"IF"を考えるという楽しみです。

一例としてこういう場面を考えます。

ある日サッカーワールドカップの試合結果を目にする―― 「ここにもしベジェルとウル・コーマが参加していたら……」―― しかし両国のサッカー事情を想像するのは難しい―― オリンピックならどうか―― 直近で開催されたのは北京開催の冬季オリンピック――

「ベジェルとウル・コーマは北京オリンピックの開会式で何番目に入場するか？」

北京オリンピックの開会式

なぜ北京オリンピックの開会式での入場順を考えるのか。それは、異なる文字文化の衝突が鮮やかに現れる場であるためです。「ベジェルとウルコーマの北京オリンピックでの入場順」は、「この2か国がどう東洋文明と干渉するか」という大きすぎて想像するには難しい"IF"の片鱗を味わうのにちょうど良い題材です。

さて、オリンピックの開会式の入場行進では、選手団が参加国・地域ごとにまとまって会場に入場します。ではその順番はどのように決まるか？

先に簡単な例として、2012年ロンドンオリンピックでの順番を見ましょう。日本の前後5か国を下表に示します。

入場順	国名（英語）	国名（日本語）
90	Iraq	イラク
91	Ireland	アイルランド
92	Israel	イスラエル
93	Italy	イタリア
94	Jamaica	ジャマイカ
95	Japan	日本
96	Jordan	ヨルダン
97	Kazakhstan	カザフスタン
98	Kenya	ケニア
99	Kiribati	キリバス
100	Republic of Korea	韓国

順番を決める規則は明らかです。英語で表記した国名のアルファベット順になっています。

ただし、重要な例外として、ギリシャ（Greece）は1番目、イギリス（Great Britain）は最後の205番目です。その他、表中にもある韓国（Republic of Korea）が "Korea" として扱われるなど、細かな例外が含まれます。

2012年ロンドンオリンピックの開会式の入場行進 - Wikipedia

この規則は、国際オリンピック委員会による指針、

代表団の入場は、開催国の言語のアルファベット順とする。ただし、ギリシャは最初に、開催国は最後に入場する。

The-opening-ceremony-of-the-Games-of-the-Olympiad.pdf

に従うものです。

アルファベット順？

では2022年冬季北京オリンピックではどうだったか。

入場順	国名（簡体字中国語）	国名（日本語）
5	马来西亚	マレーシア
6	厄瓜多尔	エクアドル
7	厄立特里亚	エリトリア
8	牙买加	ジャマイカ
9	比利时	ベルギー
10	日本	日本
11	中华台北	台湾（中華台北）
12	中国香港	香港（中国香港）
13	丹麦	デンマーク
14	乌克兰	ウクライナ
15	乌兹别克斯坦	ウズベキスタン

2022年北京オリンピックの開会式 - Wikipedia

頭文字が同じなら隣接しているので、簡体字中国語表記に何らかの順序が入っているのはまあ明らかでしょう。しかし漢字はアルファベットではない。「アルファベット順」なるものは、そもそも存在しません。

では何が基準か。

漢字の順序と言えば、日本語話者に慣れ親しまれているのは漢字辞典にあるそれでしょう。普通、日本語の漢字辞典では

康熙字典に基づく部首順
部首が同じなら、残りの部分の画数順

で漢字が順序付けられています。日本工業規格（JIS）で割り振られた番号や、それを基にしたユニコード等の規格でも概ねこの順序が採用されているため、文字に関する技術を扱う人々にとっても馴染み深いものでしょう。

ですが、北京オリンピックの入場順はそれとは異なります。日本の漢字辞典の順序ではありません。順番を決める第一の基準は、部首ではなく各文字の画数です。Wikipedia曰く、

中国語の標準漢字（簡体字）による各国国名の最初の漢字の画数の順番に行進。

というのが、ここにある規則です。「马」（「馬」の簡体字」）の3画に対して「厄」が4画だから、5番目の马来西亚（マレーシア）より後に6番目の厄瓜多尔（エクアドル）が来るというわけです。

ロンドンオリンピックでは95番目と中盤の入場だった日本も、北京では序盤の10番目です。

しかしすぐに分かる通り、画数だけでは説明の半分にもなりません。7番目の厄立特里亚（エリトリア）と8番目の牙买加（ジャマイカ）は頭文字が同じ4画。この前後関係は何から決まるか。

答えは 笔顺编号（ビーシュンビアンハオ） です[2]。日本語の新字体表記では「筆順編号」。直訳では「書き順番号」といったところです。

[2]なお公式の文書としては公開されているものが見つけられなかった。有料記事になるが、朝日新聞の記者が大会広報に問いあわせた内容が開会式の入場順のなぜ…　中国の担当者「その質問は対面で答える」 - 2022北京オリンピック：朝日新聞デジタルにある。「笔顺编号」という語こそ出てこないものの、「順番が先になるのは、横線▽縦棒▽はらい▽点▽折れ線――の順」との記述があり、以下の笔顺编号の説明と一致する。このような順序の決め方は「政府が定めた規則」である、との記述もある。

笔顺编号

笔顺编号_百度百科

日本ではあまり馴染みのない笔顺编号ですが、なかなか合理的です。「筆でどのように書くか」を基準とする点は画数と共通していますが、今度は数ではなく筆の運び方に注目します。

笔顺编号では、筆の一なぞり（1画分）を5種類に分類して1-5の番号を振ります。すなわち、横（ハン）、竖（シュー）、撇（ピエ）、捺（ナー）、折（ジョー）の5つです。

番号	名前	形	意味
1	横	一	横画
2	竖	丨	縦画
3	撇	丿	左はらい
4	捺	㇏	右はらい
5	折	㇕	折れ

筆画のひとつひとつをこの5つのうちのどれかに対応させ、画数の順に並べるとその文字の笔顺编号が得られます。

「厄」を例にして笔顺编号がどう決まるか見てみます。

「厄」は

筆番	筆形	番号
1画目	㇐	横=1
2画目	㇓	撇=3
3画目	㇆	折=5
4画目	㇟	折=5

のように書くから、笔顺编号は "1355" になります。注意として、「折れ」は向きに寄りません。

同様に、「牙」の場合、

筆番	筆形	番号
1画目	㇐	横=1
2画目	㇗	折=5
3画目	㇚	竖=2
4画目	㇒	撇=3

で笔顺编号は "1523" です。3画目にハネがありますが、これは「折れ」とはみなしません。

この2つの笔顺编号を辞書式順序で比較します[3]。すると、厄="1355" < 牙="1523" だから、「厄」は「牙」より先に来ます。

[3]画数で比較してから辞書式順序で比較しているので、実は笔顺编号を10進法表記された整数値と見て大小を比較するだけでも良い

こうして、厄立特里亚（エリトリア）が牙买加（ジャマイカ）より先に入場した理由を説明することができました。[4]

[4] ご察しの通り、画数と笔顺编号でも順序が決まらない場合がある。例えば、「力」と「刀」は両方とも画数2で笔顺编号は53。「札」が"12345"で「朰」が"12345"という衝突もある。つまり漢字全体から笔顺编号全体への写像は単射ではない。これは笔顺编号が漢字を符号化する方法としては不適格であることも意味する。

幸い、北京オリンピック開催国の異なる国名同士で、全ての文字の笔顺编号が一致するペアは存在しない。

「刀礼」国と「力朰」国の参加を想像する場合には問題になるが、あとで登場する実装では安定ソートとすることで妥協した。

なお、笔顺编号（Stroke Order Code）は以下の辞書サイトから調べることができます。

漢字と近代文明

画数も笔顺编号も「漢字に内在する性質」です。借りもののアルファベットや工業規格ではなく、それぞれの文字がそもそも持っている性質だけを利用して、漢字を整列させることができるのです。

ソートは情報処理の基本。 O(n)をO(log(n))に変える魔法の原理です。「漢字の形に基づく順序付け」が中国で考案されたのも、大量の文字データのなかから目的のものを探しあてるための「検字法」開発が源流にあります[5]。

[5]「漢字の形に基づく順序付け」は現代にも生きている。中国語キーボードの入力方式としてはピンインによるものが主流だが、「五筆字型入力方法」は本質的に笔顺编号に基づく入力法である。また日本でも、諸橋轍次による日本最大の漢和辞典『大漢和辞典』には、「四角号碼」という、漢字の形状に基づく索引が付いている。

漢字は近代化の中でたびたび廃止に向けた攻撃に晒されてきました。日本では当用漢字の制定、中国でも簡体字の制定は教育上の利便性や情報処理の効率化を目指した「漢字制限」の結果として行われたものです。

そうした歴史を踏まえると、漢字に自然な順序付けが可能であるという性質が宿っていたというのはなかなか愉快なことではないでしょうか。北京オリンピックの入場式は、漢字が近代化の波を乗り越えて生き残ったことを、高らかに世界に向けて示したのでした。

漢字と技術のせめぎあいの歴史については、トーマス・S・マラニー（比護遥訳）『チャイニーズ・タイプライター』（中央公論新社、2021年）が非常に詳しいです。

www.chuko.co.jp

漢字の欠点――あまりにも多すぎる――を克服してタイプライターを開発するためにどんなことが考えられてきたか、エキサイティングな歴史が綴られています。この項の内容も、2008年北京オリンピック入場式の描写から始まる「序論　そこにアルファベットはない」に大きく依っています[6]

[6]ただし永字八法に基づく「筆画による順序付け」の説明はややミスリーディング。永字八法に含まれる8種の筆遣いへの漢字の分割はどうにも無理がある。

ソートプログラム

規則が分かればそれをプログラムとして表現することが可能です。

えいっと書いてwebアプリにします。

技術的な概要：

笔顺编号のデータがYQ-YSY/stroke-seq_MBにある（GPLv3.0）のでこれをmapとしてRustクレートに埋め込む。
char をラップした ChineseCharacter 構造体に、そのmapを利用して PartialOrd, Ord トレイトを実装する。
ChineseCharacter の配列として文字列をソートする関数を定義する。
それを取り込んでWebAssembly（wasm）としてエクスポートする。巨大なルックアップテーブルを内包するのでちょっと時間がかかる。
ViteでReactアプリを初期化してwasmを取り込む。
Vercelへデプロイ。楽だ～～～

北京オリンピック開会式入場順ソート

ソースは

github.com

で公開しています。

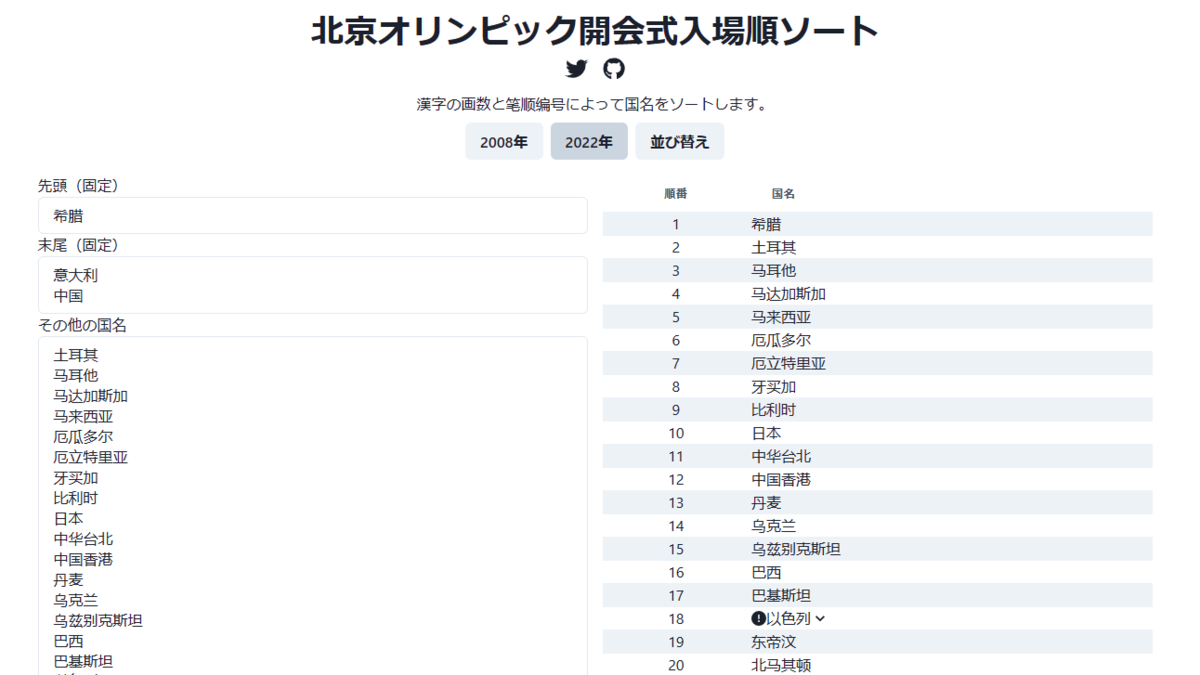
あとは入力して「並び替え」を押してやるだけです。

贝歇尓と乌库姆

ここに『都市と都市』の簡体字中国語訳『城与城』があります。

目次を開きます。

すると、日本語版の第1部のタイトル「ベジェル」、第2部「ウル・コーマ」に対応して、それぞれ簡体字版では「贝歇尓」「乌库姆」と表記されることが分かります。

贝、乌、库はそれぞれ貝・烏・庫に対応する簡体字です。「乌」はウーロン（乌龙茶）茶のウーです。「贝」も「貝」を音読みで「バイ」と読むので、何となく音が対応していることが分かります。ピンインでは贝歇尓は bèi-xiē-ěr、乌库姆は　wū-kù-mǔ となります。

英語	日本語	簡体字中国語
Besźel	ベジェル	贝歇尓
Ul Qoma	ウル・コーマ	乌库姆

ようやく初めの問い、「ベジェルとウル・コーマは北京オリンピックで何番目に入場するか？」に答える準備が整いました。

まずは2022年冬季オリンピックから。

「2022年」ボタンを押すと、現実の参加国が自動で入力されます。

希腊（ギリシャ）は先頭で固定、中国は開催国、意大利（イタリア）は次回2026年冬季オリンピックの開催国であるため、中国の1つ前です[7]。

[7]2020東京オリンピックから、将来の開催国も開催年の逆順で入場するようになった。2020年東京オリンピックの開会式 - Wikipedia

そして「その他の国名」欄に「贝歇尓」と「乌库姆」を追加します。最後に「並べ替え」をクリック。

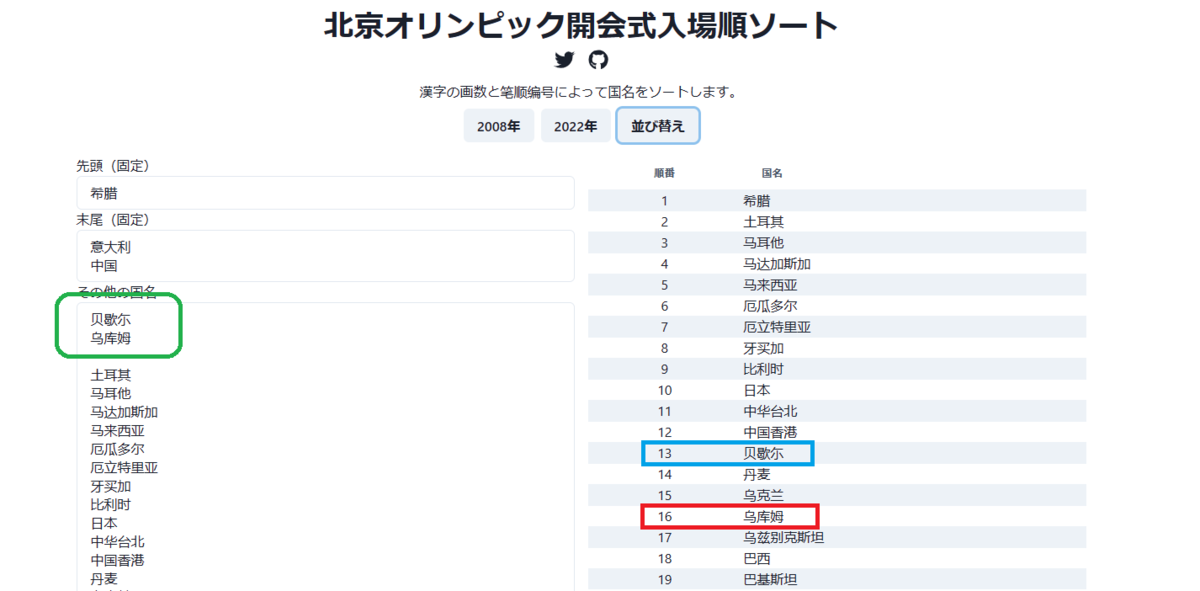
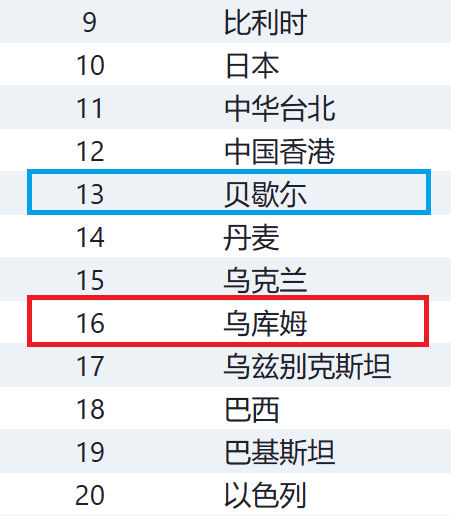
結果は、

贝歇尓は13番目で中国香港と丹麦（デンマーク）の間
乌库姆は16番目で乌克兰（ウクライナ）と乌兹别克斯坦（ウズベキスタン）の間

でした。偶然とはいえ非常に近い。

念のため笔顺编号を見ておきます。

順番	国名	各文字の笔顺编号
12	中国香港	2512, 25112141, 312342511, 441122134515
13	贝歇尓	2534, 2511353453534, 31234
14	丹麦	3541, 1121354
15	乌克兰	3551, 1225135, 43111
16	乌库姆	3551, 4131512, 53155414
17	乌兹别克斯坦	3551, 431554554, 2515322, 1225135, 122111343312, 12125111

正しく画数と笔顺编号の順序で並んでいます。乌克兰と乌库姆は1文字目が同じ、2文字目も画数まで一致するため、2画目の笔顺编号を比較して初めて前後関係が決まっています。

2008年夏季オリンピックも同様に調べると、

順番	国名（簡体字中国語）	国名（日本語）
28	贝宁	ベナン
29	贝歇尓	ベジェル
30	毛里求斯	モーリシャス
31	毛里塔尼亚	モーリタニア
32	丹麦	デンマーク
33	乌干达	ウガンダ
34	乌克兰	ウクライナ
35	乌库姆	ウル・コーマ
36	乌拉圭	ウルグアイ

のように、ベジェルが29番目、ウル・コーマが35番目になります[8]。

[8]実はプログラム通りに並べるとそれぞれこれらより1つ小さい番号に出る。どうも以色列（イスラエル）の頭文字の「以」の笔顺编号が想定の5434ではなくて2434として扱われているらしい。1画目の「㇙」を「折れ」ではなくて「縦」として扱っているということ。2022大会では想定通り5434の位置にいるので、何か基準が変わったか、単純にミスかもしれない。この他にも明らかに漢字以外の事情による例外があり、ソートのロジックに組み込むことは諦めて注として示すことにしている。

こうして、北京オリンピック開会式の入場行進のベジェルとウル・コーマの入場順が明らかになりました。まとめると、

2008年大会ではベジェルが13番目、ウル・コーマが16番目
2022年対大会ではベジェルが29番目、ウル・コーマが35番目

です。

ベジェル時間2022年2月4日の昼下がり。〈クロスハッチ〉地区のダプリールカフェにかけられたテレビは遠く中国北京で始まったオリンピックの開会式を映す。日本、台湾、香港の極東3地域が続いたあとに入場するのはベジェルの選手たち。のどかな午後を過ごしていた客たちは顔を上げる。

同時刻、ウル・コーマの総体局所的（グロストピカリー）にほど近いカフェ。甘くて濃いお茶を啜りつつスマートフォンで開会式を眺めていた客は、ベジェルの入場と〈見ない〉でいる人々のざわめきを無意識化で結びつける。デンマーク、ウクライナ――ロシアが戦争を始めるのはこの3週間後のこと――そしてウル・コーマ。今度はこちらからあちらへ、甘いシナモンの香りにのって微かなざわめきが伝わっていく。

ベジェルとウル・コーマの入場順がこんなに近付くことの珍しさに、この輪の中にいる誰かが気付くかもしれないし気付かないかもしれない。

リファレンス

China Miéville The City & The City（Del Rey、2009年）（Kindle版）
チャイナ・ミエヴィル（日暮雅通訳）『都市と都市』（早川書房、2011年）
柴纳・米耶维（胡绍晏訳）『城与城』（重庆出版社、2021年）
トーマス・S・マラニー（比護遥訳）『チャイニーズ・タイプライター　漢字と技術の近代史』（中央公論新社、2021年）
三上喜貴『文字符号の歴史　アジア編』（共立出版、2002年）

2022-05-06

十六進表記が十進法でも読めると嬉しい

十六進法で表記されたハッシュ値を扱っていると、たまに十進法でも有効な文字列になっていることがある。
つまり、十六進表記だがどの桁も0から9のいずれかで、aからfを含まないということ。実例として、

${ \begin{align} (123456)_{16} = (1193046)_{10} \end{align} }$

など。反対に、

${ \begin{align} (\rm{bc614e})_{16} = (12345678)_{10} \end{align} }$

は ${1, 5, 6}$ 桁目にそれぞれ ${\rm{e, c, b}}$ を含むため十進法で読めない。

このような性質を満たす数のことを 偽十進法整数 と呼ぶことにする。すなわち、 ${n}$ が偽十進法整数であるとは、 ${0}$ 以上 ${9}$ 以下の整数の列

${ \begin{align} a_0, a_1, a_2,\cdots, a_{m} \end{align} }$

が存在して、

${ \begin{align} n = a_0 + a_1 \cdot 16 + a_2 \cdot 16^2 + \cdots a_{m} \cdot 16^m \end{align} }$

を満たすということ。

7桁程度の偽十六進整数ならさして珍しくないことは、 ${(16)^7}$ の数のうち、割合として

${ \begin{align} \left(\frac{10}{16}\right)^6 = 0.037\cdots \end{align} }$

がこの性質を満たすことから分かる。gitのログで表示されるコミットハッシュの短縮形のデフォルト桁数がこの7桁*1なので、目にする機会も多い。

さて、偽十進法整数は具体的にどれくらい存在するだろうか。非負整数 ${n}$ 以下の非負の偽十進法整数の個数を ${p_n}$ で表すことにする。なお、特に進数表記をしていない限り以下では十進法。

${ \begin{align} \begin{array}{|r|r|} \hline n & p_n \\ \hline\hline 0 & 1 \\ \hline 1 & 2 \\ \hline 2 & 3 \\ \hline \vdots & \vdots \\ \hline 10 & 10 \\ \hline 100 & 65 \\ \hline 1000 & 400 \\ \hline 10000 & 2711 \\ \hline 100000 & 18700 \\ \hline 1000000 & 100000 \\ \hline 10000000 & 989681 \\ \hline 100000000 & 6000000 \\ \hline \end{array} \end{align} }$

${p_{n}/n}$ が ${n\rightarrow \infty}$ で ${0}$ に漸近することはほぼ明らか。では、 ${n}$ 以下の偽十進法非負整数とそうでない数が同数になるのはいつだろうか。すなわち、

${ \begin{align} n+1-p_{n} = p_{n} \end{align} }$

となるのはいつか。計算すると、 ${n=199}$ ただひとつがこの性質を満たすことが分かる。

少し一般化して、

${ \begin{align} n+1 = k\,p_n \end{align} }$

を満たすような整数 ${k}$ が存在する ${n}$ を探そう。 ${k=2}$ が上で調べた場合にあたる。 ${10^9}$ 以下での結果が下表。

${ \begin{align} \begin{array}{|r|r|r|} \hline n & p_n & k \\\hline\hline 0 & 1 & 1 \\ \hline 1 & 2 & 1 \\ \hline 2 & 3 & 1 \\ \hline 3 & 4 & 1 \\ \hline 4 & 5 & 1 \\ \hline 5 & 6 & 1 \\ \hline 6 & 7 & 1 \\ \hline 7 & 8 & 1 \\ \hline 8 & 9 & 1 \\ \hline 9 & 10 & 1 \\ \hline 199 & 100 & 2 \\ \hline 2999 & 1000 & 3 \\ \hline 3999 & 1000 & 4 \\ \hline 4151 & 1038 & 4 \\ \hline 4159 & 1040 & 4 \\ \hline 7999 & 2000 & 4 \\ \hline 8311 & 2078 & 4 \\ \hline 8319 & 2080 & 4 \\ \hline 8399 & 2100 & 4 \\ \hline 8471 & 2118 & 4 \\ \hline 8479 & 2120 & 4 \\ \hline 11999 & 3000 & 4 \\ \hline 12631 & 3158 & 4 \\ \hline 12639 & 3160 & 4 \\ \hline 12799 & 3200 & 4 \\ \hline 15999 & 4000 & 4 \\ \hline 16791 & 4198 & 4 \\ \hline 16799 & 4200 & 4 \\ \hline 16951 & 4238 & 4 \\ \hline 16959 & 4240 & 4 \\ \hline 19999 & 5000 & 4 \\ \hline 21111 & 5278 & 4 \\ \hline 21119 & 5280 & 4 \\ \hline 21199 & 5300 & 4 \\ \hline 21271 & 5318 & 4 \\ \hline 21279 & 5320 & 4 \\ \hline 23999 & 6000 & 4 \\ \hline 25431 & 6358 & 4 \\ \hline 25439 & 6360 & 4 \\ \hline 25599 & 6400 & 4 \\ \hline 27999 & 7000 & 4 \\ \hline 29591 & 7398 & 4 \\ \hline 29599 & 7400 & 4 \\ \hline 29751 & 7438 & 4 \\ \hline 29759 & 7440 & 4 \\ \hline 31999 & 8000 & 4 \\ \hline 33911 & 8478 & 4 \\ \hline 33919 & 8480 & 4 \\ \hline 33999 & 8500 & 4 \\ \hline 34071 & 8518 & 4 \\ \hline 34079 & 8520 & 4 \\ \hline 35999 & 9000 & 4 \\ \hline 38231 & 9558 & 4 \\ \hline 38239 & 9560 & 4 \\ \hline 38399 & 9600 & 4 \\ \hline 39999 & 10000 & 4 \\ \hline 49999 & 10000 & 5 \\ \hline 59999 & 10000 & 6 \\ \hline 74879 & 12480 & 6 \\ \hline 74999 & 12500 & 6 \\ \hline 119999 & 20000 & 6 \\ \hline 149999 & 25000 & 6 \\ \hline 152639 & 25440 & 6 \\ \hline 179999 & 30000 & 6 \\ \hline 227999 & 38000 & 6 \\ \hline 230399 & 38400 & 6 \\ \hline 239999 & 40000 & 6 \\ \hline 699999 & 100000 & 7 \\ \hline 799999 & 100000 & 8 \\ \hline 899999 & 100000 & 9 \\ \hline 999999 & 100000 & 10 \\ \hline 1079999 & 108000 & 10 \\ \hline 1099999 & 110000 & 10 \\ \hline 1122999 & 112300 & 10 \\ \hline 1123079 & 112308 & 10 \\ \hline 1397339 & 155260 & 9 \\ \hline 1439999 & 160000 & 9 \\ \hline 1799999 & 200000 & 9 \\ \hline 1999999 & 200000 & 10 \\ \hline 2999999 & 300000 & 10 \\ \hline 3369999 & 337000 & 10 \\ \hline 3399999 & 340000 & 10 \\ \hline 3999999 & 400000 & 10 \\ \hline 4494399 & 449440 & 10 \\ \hline 4499999 & 450000 & 10 \\ \hline 4999999 & 500000 & 10 \\ \hline 5658739 & 565874 & 10 \\ \hline 5659999 & 566000 & 10 \\ \hline 5660799 & 566080 & 10 \\ \hline 5699999 & 570000 & 10 \\ \hline 5999999 & 600000 & 10 \\ \hline 6783879 & 678388 & 10 \\ \hline 6783999 & 678400 & 10 \\ \hline 6799999 & 680000 & 10 \\ \hline 6999999 & 700000 & 10 \\ \hline 7948339 & 794834 & 10 \\ \hline 7949999 & 795000 & 10 \\ \hline 7950399 & 795040 & 10 \\ \hline 7999999 & 800000 & 10 \\ \hline 10999999 & 1000000 & 11 \\ \hline 11999999 & 1000000 & 12 \\ \hline 12999999 & 1000000 & 13 \\ \hline 13999999 & 1000000 & 14 \\ \hline 14999999 & 1000000 & 15 \\ \hline 15999999 & 1000000 & 16 \\ \hline 17279999 & 1080000 & 16 \\ \hline 17599999 & 1100000 & 16 \\ \hline 17967999 & 1123000 & 16 \\ \hline 17969279 & 1123080 & 16 \\ \hline 20215499 & 1347700 & 15 \\ \hline 20249999 & 1350000 & 15 \\ \hline 23799999 & 1700000 & 14 \\ \hline 24359999 & 1740000 & 14 \\ \hline 27999999 & 2000000 & 14 \\ \hline 29999999 & 2000000 & 15 \\ \hline 31999999 & 2000000 & 16 \\ \hline 40466249 & 2697750 & 15 \\ \hline 40499999 & 2700000 & 15 \\ \hline 44999999 & 3000000 & 15 \\ \hline 47999999 & 3000000 & 16 \\ \hline 53919999 & 3370000 & 16 \\ \hline 54399999 & 3400000 & 16 \\ \hline 63999999 & 4000000 & 16 \\ \hline 71910399 & 4494400 & 16 \\ \hline 71999999 & 4500000 & 16 \\ \hline 79999999 & 5000000 & 16 \\ \hline 90539839 & 5658740 & 16 \\ \hline 90559999 & 5660000 & 16 \\ \hline 90572799 & 5660800 & 16 \\ \hline 91199999 & 5700000 & 16 \\ \hline 95999999 & 6000000 & 16 \\ \hline 108542079 & 6783880 & 16 \\ \hline 108543999 & 6784000 & 16 \\ \hline 108799999 & 6800000 & 16 \\ \hline 111999999 & 7000000 & 16 \\ \hline 127173439 & 7948340 & 16 \\ \hline 127199999 & 7950000 & 16 \\ \hline 127206399 & 7950400 & 16 \\ \hline 127999999 & 8000000 & 16 \\ \hline 169999999 & 10000000 & 17 \\ \hline 179999999 & 10000000 & 18 \\ \hline 189999999 & 10000000 & 19 \\ \hline 199999999 & 10000000 & 20 \\ \hline 209999999 & 10000000 & 21 \\ \hline 219999999 & 10000000 & 22 \\ \hline 229999999 & 10000000 & 23 \\ \hline 239999999 & 10000000 & 24 \\ \hline 249999999 & 10000000 & 25 \\ \hline 259999999 & 10000000 & 26 \\ \hline 292499999 & 11700000 & 25 \\ \hline 292562049 & 11702482 & 25 \\ \hline 299999999 & 12000000 & 25 \\ \hline 303202499 & 12128100 & 25 \\ \hline 323447999 & 13477000 & 24 \\ \hline 323999999 & 13500000 & 24 \\ \hline 367999999 & 16000000 & 23 \\ \hline 395929599 & 17996800 & 22 \\ \hline 395999999 & 18000000 & 22 \\ \hline 417999999 & 19000000 & 22 \\ \hline 420199999 & 19100000 & 22 \\ \hline 439999999 & 20000000 & 22 \\ \hline 459999999 & 20000000 & 23 \\ \hline 479999999 & 20000000 & 24 \\ \hline 499999999 & 20000000 & 25 \\ \hline 519999999 & 20000000 & 26 \\ \hline 599999999 & 24000000 & 25 \\ \hline 606434149 & 24257366 & 25 \\ \hline 647459999 & 26977500 & 24 \\ \hline 647999999 & 27000000 & 24 \\ \hline 719999999 & 30000000 & 24 \\ \hline 749999999 & 30000000 & 25 \\ \hline 779999999 & 30000000 & 26 \\ \hline 898999999 & 35960000 & 25 \\ \hline 899027074 & 35961083 & 25 \\ \hline 899999999 & 36000000 & 25 \\ \hline 909999999 & 36400000 & 25 \\ \hline 999999999 & 40000000 & 25 \\ \hline \end{array} \end{align} }$

github.com

${n}$ は十進で下位に9が並ぶ傾向があるが、完全ではない。実際、

${n=4151, 8311, 8471}$ 等で一の位が ${1}$
${n=899027074}$ で一の位が ${4}$

となっていることが観察できる。

この「傾向」はどう説明付けられるだろうか。 ${p_n}$ の振る舞いを見よう。

${ \begin{align} \begin{array}{|r|r|r|} \hline n\,(\rm{dec}) & n\,(\rm{hex}) & p_{n}\,(\rm{dec}) \\ \hline \hline (3)_{10} & (\rm{3})_{16} & (4)_{10}\\\hline (31)_{10} & (\rm{1f})_{16} & (20)_{10}\\\hline (314)_{10} & (\rm{13a})_{16} & (140)_{10}\\\hline (3141)_{10} & (\rm{c45})_{16} & (1000)_{10}\\\hline (31415)_{10} & (\rm{7ab7})_{16} & (8000)_{10}\\\hline (314159)_{10} & (\rm{4cb2f})_{16} & (50000)_{10}\\\hline (3141592)_{10} & (\rm{2fefd8})_{16} & (300000)_{10}\\\hline (31415926)_{10} & (\rm{1df5e76})_{16} & (2000000)_{10}\\\hline (314159265)_{10} & (\rm{12b9b0a1})_{16} & (13000000)_{10}\\\hline \end{array} \end{align} }$

じっと見ると、 ${p_n}$ を簡単に計算する方法が分かる。

たとえば、

${ \begin{align} (314159265)_{10} = (\rm{12b9b0a1})_{16} \end{align} }$

以下の偽十進非負整数は、

${ \begin{align} (12999999)_{16} < (\rm{12b9b0a1})_{16} < (1300000)_{16} \end{align} }$

の関係が成り立つから、

${ \begin{align} (0)_{16}, (1)_{16}, \cdots , (12999999)_{16} \end{align} }$

の ${(1300000)_{10}}$ 個である。

言葉で説明しよう。 ${n}$ を十六進表記で上の位から見て、最初に見つかる ${9}$ より大きい文字（aからf）とそれ以下の桁の文字を全て ${9}$ で置き換えると、それが ${n}$ を超えない最大の偽十進法整数である（十六進法で読む）。その文字列を十進法で読み替えて1を加えれば ${p_n}$ を得る。

${ \begin{align} (3141592653589793238462643)_{10} &= (\rm{299421439a0abd72cb0b3})_{16} \\ p_n &= (299421439999999999999)_{10} + (1)_{10}\\ &= (299421440000000000000)_{10} \end{align} }$

という具合に。

${n+1 = k\,p_n}$ を満たす ${n}$ の下位の桁に9が並びがちな傾向はこのことから理解できる。そもそも ${p_n}$ は ${10}$ の大きな冪を約数に持ちやすく、そのため ${n=k\,p_n-1}$ は下位の桁に多くの9が並ぶ。非常に粗いヒューリスティックな議論ではあるが。

さて、未解決の問題がある。 ${n+1=k\,p_n}$ を満たす ${n}$ が、10で割って ${1,4,9}$ 以外の剰余を持つことはあるだろうか？（たぶん存在すると思う）

*1:`--abbrev` オプションで変更できる。

2022-05-03

ピンクのハートはなぜ無いか - シャニマスとユニコード絵文字（１）

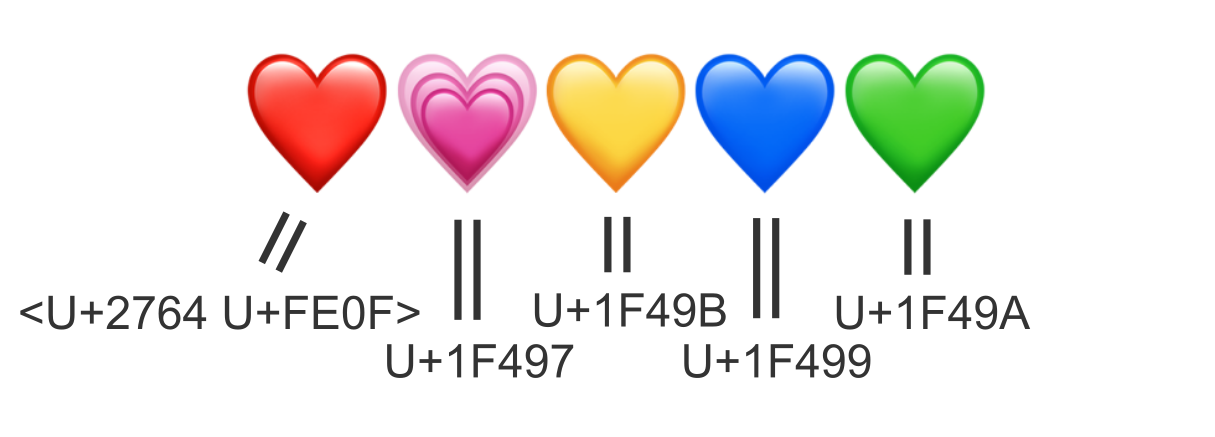
放課後クライマックスカラーのハートと符号位置 — 図1 放課後クライマックスガールズカラーのハートと符号位置

和泉愛依カラーのハート
園田智代子カラーのハート
ピンクのハートはどこに？
文字コードとは
ASCIIとJIS規格
ユニコード
絵文字
Unicode emojiへ
省略されたピンク色
赤色のハート
追加された色付きのハート
Unicode 15.0
シャニマスと絵文字
リファレンス
- 雑誌・書籍
- Webサイト

和泉愛依カラーのハート

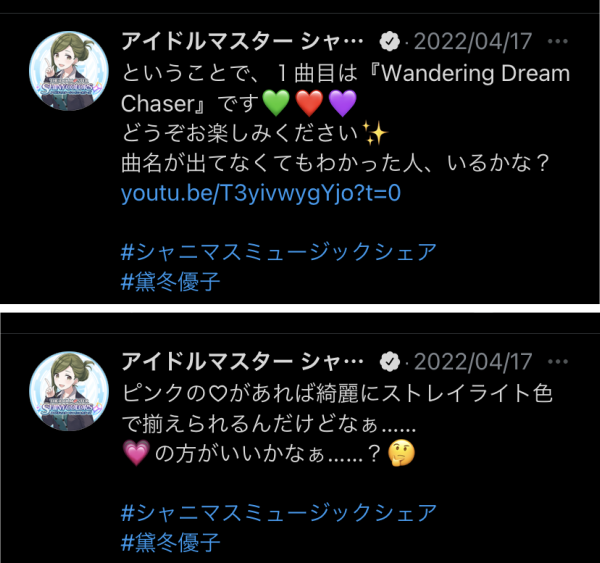
1週間後に4thライブを控えた2022年4月16日から翌17日の2日間、「シャニマスミュージックシェア」と題する、シャニマス公式ツイッター @imassc_official上での企画が行われた。内容は、ツイッター上に投稿されたファンのコメントをアイドル本人達が読み上げるという形で、過去の楽曲を紹介するというもの。

その中の一幕。ストレイライトからユニットを代表して黛冬優子が楽曲"Wandering Dream Chaser"を紹介する。

ストレイライト各メンバーのイメージカラーは、

黛冬優子: 緑
芹沢あさひ：赤
和泉愛依: マゼンタ

で、それぞれの衣装などにも取り入れられている。

Straylight (ストレイライト) | アイドルマスターシャイニーカラーズ(シャニマス)

しかし、緑と赤はあってもマゼンタに近いピンクのハートの絵文字がない。比較的色味の近い紫のハートによる代用は馴染まなかったのか、一案を講じてピンク色だが動きの付いているハート💗に変えようとしている（この後実際に一度💗にしてから再び紫に戻している）。

園田智代子カラーのハート

ピンクのハートの不在は他のユニットにも影響している。

黛冬優子の前日、放課後クライマックスガールズ（放クラ）を代表して登場した小宮果穂によるツイート。

放クラ各メンバーのイメージカラーは

小宮果穂：赤
園田智代子：ピンク
西城樹里：黄
杜野凛世：青
有栖川夏葉：緑

で、やはりこちらでもピンクが動きの付いたハート💗によって代用されている。放クラの場合、戦隊ものがオマージュ元にあるため赤とピンクははっきりと分かれているし、紫に代えることもできない。ピンクのハートの不在はストレイライトより一層重大だ。

ピンクのハートはどこに？

ピンクのハートは本当にないのだろうか。iOSの絵文字キーボードを開いてみよう。

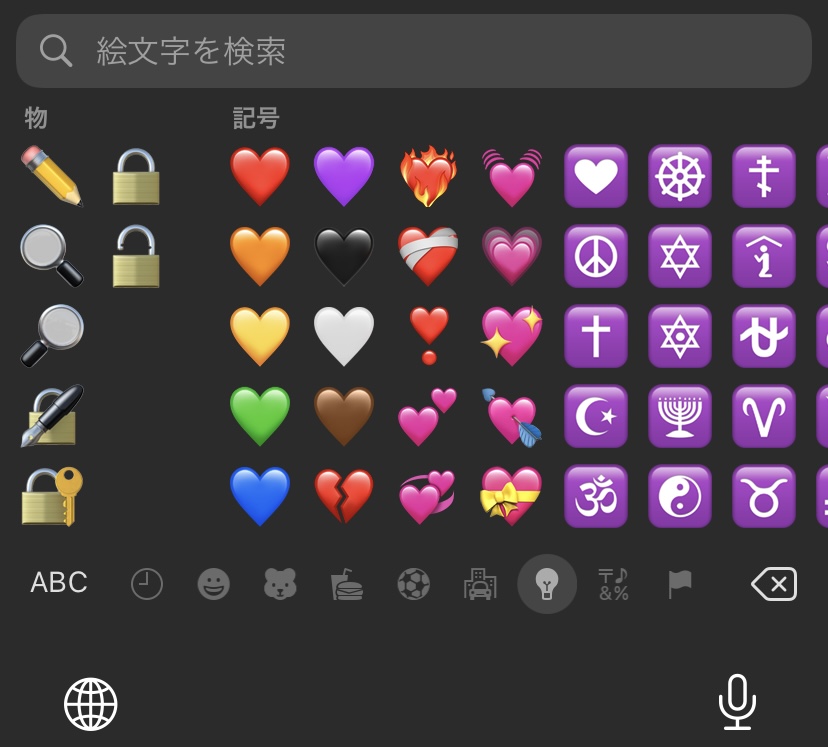
赤、橙、黄、緑、青、紫、黒、白、茶まで同じ形状のハートが並ぶ。その後に続くのは、割れていたり💔燃えていたり❤️‍🔥、特殊な形状のハートたち。そのうち、動きが付いていたり💗、キラキラしているハート💖はピンク色だが、「ただのピンクのハート」は確かにない。

ではキーボードに並んでいないだけで入力はできるのかというと、そういうわけでもない。

これは絵文字の「規格」を定めた文書からの抜粋。

The Unicode Standard, Version 14.0 p.1602（100Mと大きいので注意）

表の上ではモノクロだが、

BLUE HEART
GREEN HEART
YELLOW HEART
ORANGE HEART
PURPLE HEART

などが見て取れる。

しかし、"PINK HEART"はどこにもない。

なぜピンクのハートはないのだろうか。そしてこの「仕様」は何だろうか。

文字コードとは

歴史を辿ろう。

文字はもともと石や紙に「形」として刻まれたものを、直接人が見て認識するものだった。ところが、コンピュータで扱う（伝える・保存する・入力する……etc）には「形」そのままを扱うわけにはいかない。そこで、コンピュータの内部では0と1の列（ビット）として表現し、人の目に触れる段階になって初めて「形」として表現する方法が編み出された。これが文字の符号化である。

具体的には、例えば

十進法	二進法	十六進法	文字
0	0	00	a
1	1	01	b
2	10	02	c
…	…	…
25	11001	19	z

のようにa-zの26文字に0から順に整数値を割り当てる。

こうすれば、例えば"hello"は 07 04 0b 0b 0e というバイトの列で伝送したり保存したりすることが可能になる。こういった文字列を符号化する取り決めのことを文字コードと呼ぶ。また、ある文字に対応する数値を符号位置（コードポイント）という。たとえば、この仮想の文字コードにおいて、cの符号位置は 02、zの符号位置は 19（それぞれ16進法）になる。

文字コードは、文字をやり取りする2者の間で共有されていなくてはならない。例えば、こちらがa-zに対して0から25まで順に整数値を割り当てている一方で、相手が逆順に（aは25に、bは24に…）割り当てていれば、こちらから送った"hello"は相手側では"svool"という意味をなさない語として読み取られてしまう。 文字化けである。

もちろん、自分が作成したテキストを保存するときと読み取るときで文字コードが異なっていても困る。

ASCIIとJIS規格

文字コードが食い違うことによる混乱を避けるため、広く共有することを目的として種々の文字コードが作られてきた。

代表的かつ基本的なのは、アメリカの規格として作られたASCIIである。

ASCIIではa-zの小文字、大文字に加え、/（スラッシュ）や:（コロン）等の記号、制御文字が全て7ビットで表現されている。

すぐに気付くように、ASCIIは専ら英語を表現するために作られているため、他の言語を扱うには別の文字コードが必要になる。

日本語用の文字コードは、国内で日本産業規格（JIS）で定められた規格として作られてきた。

ASCIIをベースに、（俗にいう）半角カタカナを追加した文字コードがJIS X 0201である。全ての文字を1バイトで表すため、最大でも256文字しか含むことができず、当然漢字は表現できない。

後継のJIS X 0208は2バイトの文字コードで、 2^16=65536 という十分な広さの符号空間（文字の表現に使える数値の全体）が確保されたことで、日常的に用いられる漢字を収録できるようになった。

ユニコード

各言語用の文字コードが日本に限らず世界の各地域で策定される一方、世界中の文字を収録した一つの文字コードを作るという壮大な試みがアメリカのIT企業を中心に動いていた。ユニコードである。

ユニコードには、ラテンアルファベットベースの文字、日中韓の膨大な漢字、アラビア文字、インド系文字、様々な少数民族の言語の文字、更には古代文字が収録されている。

数学記号や音楽記号、チェスの駒♔♕♖♗♘♙やドミノのタイル🁴🀻もカバー対象。そして、絵文字を使うことができるのもこのユニコードのおかげだ。

ユニコードでは、各文字には一意な（そして一度決まれば原則的に不変の）符号位置と名前が与えられている。たとえば、

符号位置	名前	文字
U+53	LATIN CAPITAL LETTER S	S
U+3042	HIRAGANA LETTER A	あ
U+9EDB	CJK UNIFIED IDEOGRAPH-9EDB	黛
U+1F41F	FISH	🐟

といった具合に。なお、ユニコードの符号位置は、慣習的に U+ のあとに16進法で数値を置くことで表示する。

大きい符号位置を持つ傾向にあるとはいえ、ユニコードの世界において、絵文字はラテンアルファベットやひらがな、漢字と対等な存在なのだ。

絵文字

元々絵文字は日本の携帯会社が、国内規格であるJIS X 0208（をベースにした符号化方式のShift_JISなど）の未割当の領域に文字と同等の扱いにできるように割り当てたことで生まれた。公的な規格としては文字が存在しない符号位置を、企業の私的な運用を目的として利用したということ。いわゆる機種依存文字である。

2000年代初頭、当時は通信速度の制約が大きく、今でいう「スタンプ」のように画像をやりとりするのは困難だったため、その解決策としてはうまくいった。携帯メールの爆発的な普及に伴い絵文字も浸透し、コミュニケーションに欠かせない要素になるまでにそう時間はかからなかった。

しかし、絵文字はあくまでも各企業の私的な規格である。公的な規格でも統一の業界ルールでもないため、キャリアを跨ぐやりとりは文字化けを引き起こす。これを解消するため、企業間で絵文字の変換ルールが定められた。この方法はまずまずうまくいった。とはいえ、いわば各社用の独自の文字コードが乱立したままであることに変わりはなく、状況は混沌としていた。

Unicode emojiへ

キャリア各社がめいめいに絵文字を実装してた混乱の中にグーグルが踏み込んでくる。モバイル版gメールを提供するためである。

日本の誰が絵文字を表示してくれないメールを使うだろうか？それほどまでに絵文字は普及していた。日本のユーザーに使ってもらうためには何としても絵文字を扱う必要がある。

ユニコードを策定する団体、ユニコード・コンソーシアムにおいて主導的な立場にあるグーグルは、国際規格であるユニコードに絵文字を組み込むことを提案した。これは実は兼ねてよりキャリア各社も求めていたことであった。私的な規格に過ぎないため当初は却下されてしまったが、絵文字の普及とグーグルの参入によって遂に検討されるに至った。 2007年のことである。

絵文字の収録においては、それまでに使われていたキャリア各社の絵文字との互換性の維持が大前提とされ、既存の仕様で区別されているものはユニコードでも引き続き区別されることが提案の基礎となっていた。日中韓の漢字の字体を統合してきたユニコードの世界において、これは破格の好待遇を求めるようなものだった。

省略されたピンク色

グーグルによる提案に含まれるデータが公開されている。

L2/08-080 Emoji Proposal Data (PDF)

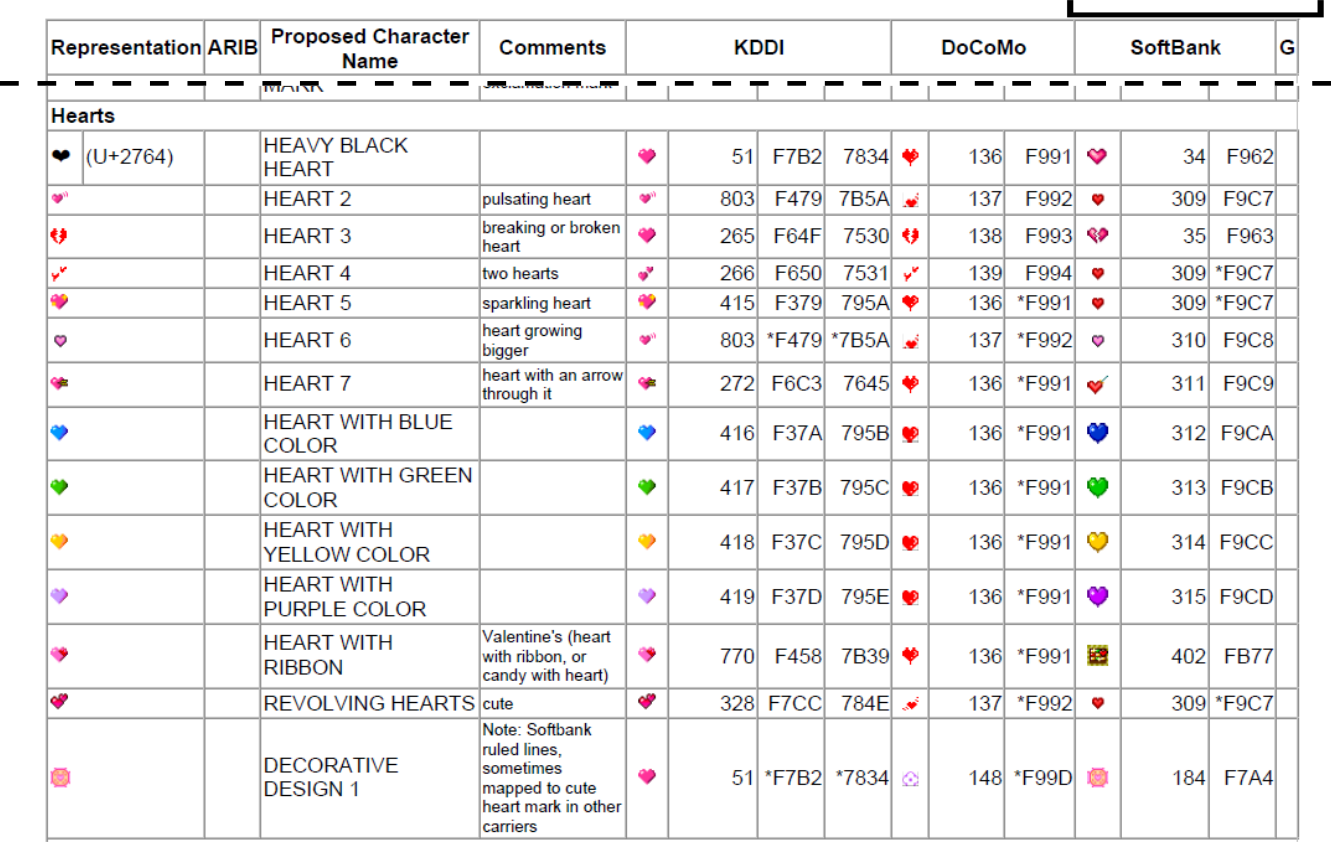
その中から、ハートの絵文字について記された箇所を加工の上抜粋した（図7）。右半分にKDDI・DoCoMo・SoftBank3社の絵文字が並んでいる。 "Representation"の列は3つを代表する形、"Proposed Character Name"はユニコードに登録する際の文字名の案が書かれている。

青・緑・黄・紫のハートはそれぞれ HEART WITH （色名） COLOR の名前を付けてユニコードに含めることが提案されている。この4つはKDDI、SoftBankで絵文字が存在することに対応したもの。 DoCoMoは対応するものがないが、変換ルール上すべて赤っぽいハートで代用されていたことが分かる。

一方、表の項目1行目、3社がピンク～赤色のハートとして表現していたものは、左端で黒塗りのハートで表現されている。付記されたU+2764は"HEAVY BLACK HEART"という当時既に存在していた飾り文字を示している。

そう、ピンク～赤色のハートの絵文字は「ベースライン」のハートであるため、その色は提案の段階で無視されることになったのだ。これはいたずらに文字を増やさないために、同一視できるものは統一するというユニコードの基本的な方針に則ったもの。漢字の数多ある字体もこの原則に従って可能な限り統合されている*1。「ベースライン」のハートと青色のハートの区別は保たれるから、互換性維持の方針には反していない。

結局、提案は若干の修正を受けた後、

符号位置	名前	文字
U+1F499	BLUE HEART	💙
U+1F49A	GREEN HEART	💚
U+1F49B	YELLOW HEART	💛
U+1f49D	PURPLE HEART	💜

として他の数百の絵文字とともに色付きのハートたちが登録されることになった。上で見た「規格」はこの時決まったもの。 Unicodeバージョン6.0、2010年のことである。

赤色のハート

ところで、赤色のハートはどこにあるのだろうか。

そもそも、ユニコードの仕様では色についてカラーコード等で明確に定めていない。あくまでも参考情報として名前に色名が付いているだけである。形でさえも「例示字形」といって「だいたいこんな形」と示されているだけで、具体的なデザインはフォントの作成者に任されている。

上述の通り、「基本」のハートの絵文字は既に存在していたU+2764 "HEAVY BLACK HEART" と統合された。しかし「絵文字らしい」ハートも欲しい。

そこで、漢字の異体字と同じ仕組みで、それ自体は表示されない*2特殊な文字、異体字セレクタによってテキストスタイルと絵文字スタイルの記号を出しわける方法が考案された。具体的には、U+2764 の直後に U+FE0F を置くと「絵文字らしい」ハートになることが決められている。一方、U+FE0Eなら黒塗りのハートのままだ（図8）。

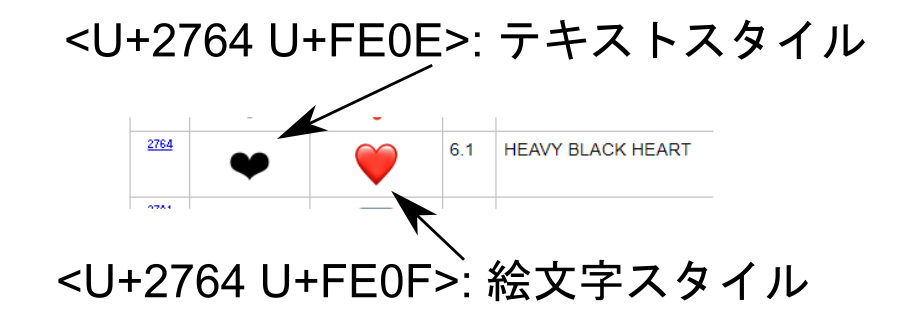
参考：Emoji Presentation Sequences, v14.0

この、絵文字スタイルの "HEAVY BLACK HEART" が普通赤色のハートとして利用されているものである。

日本と欧米の文化的な差だろうか、確かなところは分からないが「普通の」ハートは赤色と決まってしまったらしい。

Unicode emojiを網羅的に収録している辞書的なウェブサイト、Emojipediaの"red heart"の項目を見ると、Apple, Google, Twitterなど、絵文字用のフォントのほとんどの実装で赤色をこの<U+2764 U+FE0F>の組合せに当てていることが分かる。

その一方、U+1F497 のGROWING HEART（大きくなるハート）💗やSPARKLING HEART（きらきら輝くハート）💖は元になった携帯電話の絵文字を踏襲してかピンク系が付けられているものが多い。小宮果穂や黛冬優子のツイートでピンクを表現するために代用されていたのがこのGROWING HEARTのほうだ。

追加された色付きのハート

明示的に色が指定されたハートの絵文字は、最初は青・緑・黄・紫の4つだったが、その後、携帯電話の絵文字にはなかった黒・橙・白・茶が追加されて8つとなっている。

符号位置	名前	文字	追加されたバージョン
U+1F5A4	BLACK HEART	🖤	9.0
U+1F9E1	ORANGE HEART	🧡	10.0
U+1F90D	WHITE HEART	🤍	12.0
U+1F90E	BROWN HEART	🤎	12.0

参考：What Every Heart Emoji Really Means

現行のUnicodeのバージョンは14.0で、既にTwitter等でもよく見るようになった U+1FAF6 HEART HANDS🫶（【きゅん♡コメ】八宮めぐる）や U+1FAE0 MELTING FACE🫠 がこのバージョンで新しく加わっている。

参考：What's New in Unicode 14.0

オレンジ色のハートを追加するための提案に含められた理由の一つが虹を構成するために欠けた色だったことであったことは注目に値する。紫💜青💙緑💚黄💛橙🧡赤❤の6色で虹ができるということ。 283プロの7ユニットのカラーで虹を作りたい我々にとってはこれでは足りない。やはりアルストロメリアのピンクだけが欠けている。

ではピンク色のハートはどうなっているかというと、一般ユーザーの根強い要望にもかかわらず、最新のバージョン14.0でも追加はならなかった。

以上が黛冬優子のツイート

ピンクの♡があれば綺麗にストレイライト色で揃えられるんだけどなぁ……

💗の方がいいかなぁ……？🤔

の裏にある歴史的背景である。簡単にまとめると、

Twitter上では文字コードとしてユニコードの使用が前提となっている
ユニコードには日本で携帯電話メールを提供する三大キャリア（DoCoMo・au・SoftBank）の絵文字が取り込まれた
青・緑・黄・紫色のハートはauとSoftBankを引き継いで独自の色を持つものとみなされた一方、ピンク～赤色は「ベースライン」のハートとみなされた
その結果、ユニコードにおいてピンク色のハートの絵文字は仕様として定められず、絵文字スタイルのハートは専ら赤に塗られるようになった

ということ。ゲーム本編ではないとはいえ、キャラクターが実在の規格に起因する事情に言及する貴重なシーンである。

「ガラケー」はもはやアニメや漫画のキャラクターが持つことはなくなった。けいおん！！22話で中野梓が先輩4人からの合格の報せを桜の絵文字4つで表したシーンは、理解に歴史学的な知識を要するものになりつつある。そんな時代の名残がこうして黛冬優子のツイートに現れているとは、何とも奇妙で面白いことのように思う。

Unicode 15.0

さて、この記事を書いている時点でピンクのハートの絵文字は存在しない。しかし状況は変わりつつある。

Emojipediaの記事 "Pink Heart Emoji Might Finally Become Reality"（ついにピンク色のハートの絵文字が実現するかもしれない）では、ユニコードの次期バージョン15.0にピンク・グレー・薄青の3色のハートが追加される事に関して、かなり希望的な観測が述べられている。順調にいけば2022年9月に正式に発行され、その後半年程度で各プラットフォームがそれに対応したフォントを実装していくことになる。

背景にあるのは、この3色がハートの絵文字たちによるの色相環上の空白地帯になっていることや、ハートによって所属やアイデンティティを表現するという需要の高まり。青と黄のハート💙💛でウクライナへの連帯を表すという用途は一度ならず目にしたことだろう。

ピンクのハートを表現できないという悩みもまた、1年以内に過去のものになるかもしれない。

シャニマスと絵文字

シャニマスは他のツイッター上の企画（特に2021年8月30日のノクチルツイッター企画以後）でも積極的にユニコード絵文字を利用している。次の記事ではシャニマスがユニコード絵文字をどう取り込んでいるか、他の実例を見る。

リファレンス

雑誌・書籍

矢野啓介『［改訂新版］プログラマのための文字コード技術入門』（2019年、技術評論社）
小林龍生『ユニコード戦記　文字符号の国際標準化バトル』（2011年、東京電機大学出版局）
グレッチェン・マカロック（千葉敏生訳）『インターネットは言葉をどう変えたか　デジタル時代の〈言語〉地図』（2021年、フィルムアート社）
小形克宏「絵文字のユニコード符号化をめぐって」『日本語学』、vol.31、no.2、pp.44-65（2012年、明治書院）

Webサイト

小形克宏「特集 : 絵文字が開いてしまった『パンドラの箱』」、2022年5月3日閲覧
UTS #51: Unicode Emoji、2022年5月3日閲覧
Unicode Symbols、2022年5月3日閲覧
📙 Emojipedia — 😃 Home of Emoji Meanings 💁👌🎍😍、2022年5月3日閲覧

*1:とはいえ、慣習上別の字として扱われる「桜」と「櫻」は区別されているし、異体字セレクタで微妙な差異を表現するための方法も用意されている。

*2:こういった表示上の幅がなく、他の文字と組み合わせて一つの単位となるような文字の存在がユニコードで「文字数」を数えることを難しくしている。人が見て「1文字」と認識する単位のことを書記素クラスタという。カーソルの移動一つ分は書記素クラスタ1個分になる。書記素クラスタはユニコードの仕様として厳密に定まっているため、適切なライブラリさえ使えば問題は回避できる。

2021-12-30

西暦13446204年には素数がない

物理・数学 Rust

この記事はなに
用語の約束
経緯
適当な数の総積による構成
中国剰余定理
- 全ての日に制約（367桁）
- 関係式を減らす + 乱択（~9桁）
0から探す（8桁：13446204）
なぜこんなに小さいか？

この記事はなに

グレゴリオ暦の年月日を十進法で表現された数として読むと素数になることがある（例：2022年1月3日→20220103は素数）。グレゴリオ暦が未来永劫に有効であるとして、このような素数が含まれない年は13446204年に初めて訪れる。本記事では、この値を最終的に発見するまでに試みた探索の過程を説明する。

コードは
github.com
に上げています。

バージョンは、

Rust: 1.55.0
Python: 3.8.10

用語の約束

素数日
年月日を十進法で読むと素数になる日。上述の2022年1月3日など。各年の素数日の数の列が A296008 - OEIS に登録されている。

合成数日
年月日を十進法で読むと合成数になる日。2021年12月28日は明らかに合成数日である。

無素数年
素数日を含まない年（その年の全ての日が合成数日である年）。13446204は最初の無素数年である。

「グレゴリオ暦」
歴史的にはグレゴリオ暦は1582年に導入されている。また、日付と時刻に関する国際規格であるISO8601では9999年以降の扱いに関しては定めていない。本記事で「グレゴリオ暦」（西暦）という場合、西暦0年から無期限にこの暦法が適用されると仮定する。すなわち、各月に含まれる日数や閏年・閏日に関する扱いは現状に準じる*1。なお、負数（紀元前）は考えない。

経緯

@tsujimotterさんによる記事「カレンダーの上の素数〜素数には毎年出会えるか？〜」において、年月日を十進法で読んだときに素数になる日（以下「素数日」）を含む個数の期待値が1を下回る年の見積もりとして、 ${10^{154}}$ 年が与えられている。

tsujimotter.hatenablog.com

最初の目標は、具体的に無素数年を構成することでこの評価を改良することにあった。

ところが、計算を進めるうちにこの上限がどんどん下がり、愚直な探索で最初の無素数年が見つけられることが判明、ついに13446204が実際に最初の年であることが分かった*2。

結果としては最初から愚直な探索を回せばよかったものの、この宝石探しそれ自体が楽しいものだった。そのツイートを見てくださったtsujimotterさんご本人からもコメント*3をいただき、簡単にまとめることにした。

適当な数の総積による構成

具体的に無素数年を探していく。年 ${y}$ に対して、 ${10000\, y + d}$ が全て合成数なら無素数年になる。ただし、 ${d}$ はmmdd形式の月日を十進法で読んだ数で、具体的には（カレンダーを書き下すだけだが）平年（common year）なら以下の ${D_{\rm common}}$ の要素。

${ \begin{aligned} D_{\rm common} = \{ & 101, \cdots , 131, 201, \cdots , 228, 301, \cdots , 331,\\ & 401, \cdots , 430, 501, \cdots, 531, 601, \cdots, 630,\\ & 701, \cdots, 731, 801, \cdots, 831, 901, \cdots, 930, \\ & 1001, \cdots, 1031, 1101, \cdots, 1130, 1201, \cdots, 1231 \} \end{aligned} }$

閏年（leap year）なら、閏日に対応する ${229}$ を加えて、 ${D_{\rm leap}}$ の要素を取る。

${ \begin{align} D_{\rm leap} = D_{\rm common} \cup \{ 229 \} \end{align} }$

つまり、年 ${ y }$ が平年か閏年かに応じて、

${ \begin{align} Y_{t} &= \left\{ 10000\,y + d \mid d \in D_{t} \right\} & (t = {\rm common}, {\rm leap}) \end{align} }$

で定義される ${ Y_{t} }$ の要素すべてが合成数になればよい。

アプローチのひとつは、 ${y}$ が全ての ${d}$ と2以上の公約数を持つような ${y}$ を作ることである。

1231 !（3272桁）

コード

まず、無素数年の自明な例として ${1231!}$ がある。実際に計算すると、

${ 1231! \simeq 2.7 \times 10^{3271} }$

と3272桁の無素数年が得られる。こうして無素数年が存在することが示された。

mmddの総積（1001桁）

コード

階乗による構成は明らかに無駄を含んでいる。2月30日は存在しない*4 から、積を取るとき 230 は除外してよい。

平年のmmddすべての積を

${ y = \prod_{d \in D_{\rm common}} d \simeq 8.2 \times 10^{1000} }$

によってとると、1001桁の無素数年になる。なお、平年を取ったのは、こうして得られる数が明らかに400で割り切れるから。

2か5の倍数を除いたmmddの総積（412桁）

コード

20211230, 20220102, 20220105, ...は明らかに合成数。 ${d}$ が 2 または 5 を約数に持てば、 ${10000\,y+d}$ もそれを約数に持つため。だから、積から 2 か 5 の倍数は除いてもいい。

${ E = \{ d \in D_{\rm common} \mid {\rm gcd}(d,10) = 1 \} }$

として ${E}$ の総積を取ると、

${ y = \prod_{d \in E} d \simeq 2.3 \times 10^{411} }$

と412桁の無素数年が得られる。

1より大きい最小の公約数のみ共有（167桁）

コード

積を取る中で、 ${d}$ それ自体を掛ける必要はない。たとえば、 ${d=119=7 \cdot 17}$ は、 ${y}$ との公約数として7だけを共有していればよい。

また、順に掛けていくと、 ${309=3\cdot 103}$ の約数3は、 ${111 = 3\cdot 37}$ が現れた時点で積に取り込まれているから追加する必要がない。

この方法で計算すると、

${ y \simeq 1.0 \times 10^{166} }$

が得られる。

なお、構成法から明らかなように、この ${y}$ は無平方数である。

乱択アルゴリズム（~12桁）

コード

律儀にすべての ${d}$ との1より大きい公約数が存在することを保証する必要はない。適当な割合の月日に対してのみ ${y}$ と mmdd 部分が公約数を持つように条件を課し、残りの月日に対しては素数判定（ミラー・ラビンテスト）を行って、もし素数日が存在しなければ無素数年として採択すればよい。「適当な割合」の取り方によるが、0.08程度（約ひと月）あれば無素数年がある程度効率よく得られるようになる。この方法で実際に

${ y = 8333538029817 \simeq 8.3 \times 10^{12} }$

という無素数年が得られた。かなり小さくなってきた。

中国剰余定理

ここで少しアプローチを変える。 ${10000\,y+d}$ がある素数 ${p}$ で割り切れるようにするために ${p}$ それ自体を掛ける方法では、積がどんどん膨らむためなかなか小さな値は得られない。もっと直接的に、 ${10000\,y+d \equiv 0 \mod p}$ という条件を課すほうが小さい値が得られる見込みは高いだろう。

全ての日に制約（367桁）

コード

各年月日がある（小さい）素数で割り切れるという制約を課して、その条件を満たす整数を求める。具体的には、

${ \begin{align} 10000\,y + 101 &\equiv 0 \mod 3, \\ 10000\,y + 103 &\equiv 0 \mod 7, \\ 10000\,y + 107 &\equiv 0 \mod 11, \\ &\vdots\\ 10000\,y + 1231&\equiv 0 \mod 881 \end{align} }$

を解く。これを満たす最小の正整数 ${y_0}$ は、 ${q = 3\cdot 7\cdot 11\cdots 881 \simeq 5.0 \times 10^{366} }$ 未満に唯一存在することが中国剰余定理から保証されている。

なお、閏日は条件から除いておく。もし閏日（ ${10000\,y_0+229}$ ）が素数になってしまった場合、平年の素数日として ${y_0+q}$ を取れる。

さて、実際に計算すると、

${ \begin{align} y_0 = &295382390962668722563792435480\\ &899792605764414366208510569992\\ &787810541575804048893785866617\\ &574319670744354100753850262831\\ &054931517126474879283172086016\\ &931479238343604231305828997867\\ &194049155030897841192783906031\\ &461535042719576219528156266868\\ &338484803671561776298485263002\\ &290983623162932036881744610814\\ &340176502317363191226783167702\\ &596512017606064495502847995997\\ &4119552\\ \simeq&3.0 \times 10^{366} \end{align} }$

と定まる。明らかに閏年だが、幸いにも ${10000y + 229}$ は素数である。

条件をシャッフルして

${ \begin{align} 10000\,y + 101 &\equiv 0 \mod 461, \\ 10000\,y + 103 &\equiv 0 \mod 101, \\ 10000\,y + 107 &\equiv 0 \mod 43, \\ &\vdots\\ 10000\,y + 1231&\equiv 0 \mod 19 \end{align} }$

などとすれば ${y_0}$ は変わるが、 ${q}$ を上限として ${10^{366}}$ オーダーに留まるため、あまり改善しない。

関係式を減らす + 乱択（~9桁）

コード

${10000\,y+101}$ が3の倍数なら ${10000\,y+107}$ は自動的に3の倍数になる。だから、 ${10000\,y+101}$ が3の倍数になるように条件を課したなら、 ${10000\,y+107}$ に関する条件は不要になる。

さらに、総積による方法で用いたのと同様、すべての月日に対して条件を課す必要はない。適当な閾値を定めて、解いた後でそれが無素数年であれば採択、そうでなければ再試行すればよい。

肝は「適当な閾値」の取り方にある。条件に課す素数の範囲としてもよいし、条件が課されない月日の数にとってもよい。

一例として、 ${\mod 29}$ までの制約を課すとすると、100万回程度の試行で

${ \begin{align} 10000\,y+221 &\equiv 0 \mod 3,\\ 10000\,y+1003 &\equiv 0 \mod 7,\\ 10000\,y+601 &\equiv 0 \mod 11,\\ 10000\,y+813 &\equiv 0 \mod 13,\\ 10000\,y+817 &\equiv 0 \mod 17,\\ 10000\,y+327 &\equiv 0 \mod 19,\\ 10000\,y+1027 &\equiv 0 \mod 23,\\ 10000\,y+619 &\equiv 0 \mod 29\\ \end{align} }$

という連立方程式から

${ \begin{align} y = 405956995 \simeq 4.1 \times 10^8 \end{align} }$

が見つかった。西暦4億年。太陽が赤色巨星になるより前だ。

ちなみに後で行った計算で、この405956995は122番目の無素数年であることが分かった。かなりいい線を行っている。

10の8乗？　このあたりで、無素数年がずいぶん小さい領域に存在することに気付く。

ここまでの目的は構成的に無素数年を発見することで、最初の無素数年の上限を改良することにあった。なるべく小さい無素数年を探すゲーム。ところが、10の8乗オーダーの無素数年が見つかったとなると問題は違った局面に入る。ひょっとすると、0年から順に探せば最初の無素数年が見つかるのでは？

0から探す（8桁：13446204）

コード

西暦0年から探していくだけ。特に工夫もない。

手元の1.8GHzのマシンで1秒に10万年調べられる（！）ので、実は2分程度で見つかる。10時間かかるとかならともかく……最初からこれを試すべきだったのでは？（後からでは何とでも言える）

コードと……

use primeless_year::*;
use rug::Integer;

fn main() {
    for y in 0.. {
        let y = Integer::from(y);
        if y.is_probably_primeless_year() == IsPrimelessYear::Yes {
            println!("{}", y);
            break;
        }
    }
}

出力：

13446204

こうして西暦1344万6204年が最初の無素数年であることが分かった。閏年だ。

ここまで小さいと愚直な素因数分解も簡単にできて、実際にすべての月日が合成数日であることが確かめられる。しかも64ビット整数の範囲内で。

西暦13446204年の各月日の素因数分解

この中で、

${ \begin{align} 134462040331&=328343\cdot409517,\\ 134462040403&=240197\cdot559799,\\ 134462040529&=171553\cdot783793,\\ 134462040731&=257717\cdot521743,\\ \end{align} }$

あたりは2つの素因数がどちらも6桁でいい感じだ。ちなみに ${13446204}$ 自身は

${ \begin{align} 13446204 &= 2^2\cdot 3\cdot 1120517 \end{align} }$

と素因数分解される。

なぜこんなに小さいか？

13446204は小さい。こういう類の問題で、whileループで網羅的に調べられるというあまりにも「ちょうどよい」範囲に答えがあるとは予想していなかった。

無素数年はこの後にも

${ \begin{gather} 13446204,\\ 27789755,\\ 30730255,\\ 36076657,\\ 40882247,\\ \vdots \end{gather} }$

10億以下の無素数年のリスト（485個ある）

とおおよそ1000万年に1回のペースで続き、決して最初の無素数年だけが例外的に小さいわけではない。

答えが見つかったいま、新しい問題が付け加わる。「なぜこんなに小さいか？」

OEISに「n個以上の合成数が連続する区間の最小の数」の列が登録されている。たとえば、合成数が6個以上連続する最初の区間は90,91,92,93,94,95で、その次の96も合成数だから、 ${a_6=a_7=90}$ 。

Smallest start for a run of at least n composite numbers.
A030296 - OEIS

リストに登録されているように、 ${a_{365}=10726904660\sim 10^{10}}$ 。最小の無素数年 ${y_{\rm min} =13446204}$ に対して、 ${10000\,y_{\rm min} \sim 10^{11}}$ だから、ほぼオーダーは同じ。素数定理で大雑把には見積もれるはずだがちょっと自信がない。今後の課題。

*1:つまり、400で割り切れるか、4で割り切れて100で割り切れない年のみ2月29日が追加される。

*2:この小ささから察せられる通り、結果としては既知のものだった。https://math.stackexchange.com/questions/3488712/is-there-a-prime-every-year-if-yyyymmdd-is-treated-as-a-base-10-number やhttps://twitter.com/potetoichiro/status/1344307093503844352 など。

*3: https://twitter.com/tsujimotter/status/1475327097279512579

*4:架空の日付 - Wikipedia

2021-07-07

『正多面体と素数』の計算をしましょう(7)─正八面体・正二十面体と保型形式

物理・数学

shironetsu.hatenadiary.com

続き．今回の記事は軽量なGitHub Pagesに上げることにしました．

shironetsu.github.io

これは何
はじめに
正八面体の場合
- 正八面体多項式
- 指標理論
- 保型形式とテータ定数
- Broué–Enguehard 写像と重み枚挙多項式
- レベル4の主合同部分群
正二十面体群の場合
- 正二十面体方程式
- ロジャース・ラマヌジャン恒等式
- 正二十面体と保型形式
- ラマヌジャンの連分数の特殊値
- レベル5の主合同部分群
- 分割数
まとめと展望
References

概要

二項正 ${n\,(n=8,\,20)}$ 面体の作用で高々 ${\pm 1}$ の定数倍の変化しか受けない正 ${n}$ 面体多項式と ${SL(2,\mathbb{Z})}$ の保型形式は，主合同部分群に関する保型形式によって結びつく．この繋がりを紐解く過程で現れるのは， ${2}$ 元線形符号の重み枚挙多項式，ロジャース・ラマヌジャン恒等式，ラマヌジャンの連分数など、種々の興味深い数学的対象である．

2021-05-26

フルーツ・パズルをSageMathで解く――楕円曲線論初歩

物理・数学

これは何
「95%の人が解けない問題」
SageMathで楕円曲線論
ねじれ部分
フルーツ・パズルの発祥はどこ？
References

これは何

「95％の人が解けない問題」とされるインターネットミームに書かれた方程式は、見た目に反して背景に楕円曲線がある難問で、この記事ではSageMathという数式処理システムを利用して解いてみた。

SageMath Notebookを以下のページに上げています。

github.com

「95%の人が解けない問題」

https://qph.fs.quoracdn.net/main-qimg-5b0690e302a38cf2a8068158199e7a21-c

Figure 1. 95% of people cannot solve this! <equation> Can you find positive whole values for :apple:, :banana:, and :pineapple:?

記事タイトルのフルーツ・パズルとはFig. 1で問われているパズルのこと。数年前にミーム化した画像なので知っている人も多いだろう。自分はTwitterで知ったはず。要は
\begin{align}
\frac{X}{Y+Z} + \frac{Y}{X+Z} + \frac{Z}{X+Y} = 4
\end{align}の正整数解 ${(X,\,Y,\,Z)}$ を見つけよ、という問題で、煽り気味に「95%の人が解けない！」という文句が付いている。しかし、実のところ見た目に反して「頭の体操」で済む難度の方程式ではない。実際、最小の解は
\begin{align}
X &= 4373612677928697257861252602371390152816537558161613618621437993378423467772036 \simeq 4.4 \times 10^{78},\\
Y &= 36875131794129999827197811565225474825492979968971970996283137471637224634055579 \simeq 3.7 \times 10^{79},\\
Z &= 154476802108746166441951315019919837485664325669565431700026634898253202035277999 \simeq 1.5 \times 10^{80}
\end{align}
と非常に巨大な数になる。

こんな大きな整数が一体どうやって見つかるのだろうか？　 ${X,\,Y,\,Z}$ の3重ループで探索すれば、整数解としては ${(X,Y,Z)=(-1,4,11), (-5,9,11)}$ などが見つかる。しかし正の解にたどり着くには、その前に太陽の寿命が尽きてしまう。

このフルーツ・パズルには既に優れた解説がいくつもある［1-5］。特に論文”"An unusual cubic representation problem"［3］には、より一般的な形の ${a/(b+c)+b/(c+a)+c/(a+b)=N}$ の整数解に関する包括的な議論がある。

鍵は楕円曲線だ。いずれの解説でも、楕円曲線上の有理点を計算する問題へと翻訳するという点で、求解の手順は基本的に一致している。概要を述べよう。