フルーツ・パズルをSageMathで解く――楕円曲線論初歩

これは何

「95％の人が解けない問題」とされるインターネットミームに書かれた方程式は、見た目に反して背景に楕円曲線がある難問で、この記事ではSageMathという数式処理システムを利用して解いてみた。

SageMath Notebookを以下のページに上げています。

github.com

「95%の人が解けない問題」

Figure 1. 95% of people cannot solve this! <equation> Can you find positive whole values for :apple:, :banana:, and :pineapple:?

記事タイトルのフルーツ・パズルとはFig. 1で問われているパズルのこと。数年前にミーム化した画像なので知っている人も多いだろう。自分はTwitterで知ったはず。要は
\begin{align}
\frac{X}{Y+Z} + \frac{Y}{X+Z} + \frac{Z}{X+Y} = 4
\end{align}の正整数解 を見つけよ、という問題で、煽り気味に「95%の人が解けない！」という文句が付いている。しかし、実のところ見た目に反して「頭の体操」で済む難度の方程式ではない。実際、最小の解は
\begin{align}
X &= 4373612677928697257861252602371390152816537558161613618621437993378423467772036 \simeq 4.4 \times 10^{78},\\
Y &= 36875131794129999827197811565225474825492979968971970996283137471637224634055579 \simeq 3.7 \times 10^{79},\\
Z &= 154476802108746166441951315019919837485664325669565431700026634898253202035277999 \simeq 1.5 \times 10^{80}
\end{align}
と非常に巨大な数になる。

こんな大きな整数が一体どうやって見つかるのだろうか？　 の3重ループで探索すれば、整数解としては などが見つかる。しかし正の解にたどり着くには、その前に太陽の寿命が尽きてしまう。

このフルーツ・パズルには既に優れた解説がいくつもある［1-5］。特に論文”"An unusual cubic representation problem"［3］には、より一般的な形の の整数解に関する包括的な議論がある。

鍵は楕円曲線だ。いずれの解説でも、楕円曲線上の有理点を計算する問題へと翻訳するという点で、求解の手順は基本的に一致している。概要を述べよう。

『正多面体と素数』の計算をしましょう(6)―正二十面体多項式と10n±1型整数

shironetsu.hatenadiary.com

つづき。今回は前々回の予想を計算機的に検証していく。

予想とはこうだ：

予想

奇素数 と正整数 に対して、 が
\begin{gather}
q \equiv \pm 1 \mod 10,\\
q\neq 9,81
\end{gather}であるとする。 に関する 次同次多項式であって、次の3つの性質を満たす が存在する。

性質(1) 二項正二十面体群 による作用で不変：
\begin{align}
f(x,y) &= f(ax+by, cx+dy),\, &
\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}
\in \widetilde{\mathcal{I}}.
\end{align}

性質(2) に関する最高次の係数は 。

性質(3) の項の係数 は全て整数で、
\begin{align}
{\rm ord}_p(c_{ij}) + {\rm ord}_p(i) + {\rm ord}_p(j) \geq {\rm ord}_p(q) =k
\end{align}を満たす。ただし整数 に対して、 は が で割り切れる回数（ で とする）。特に の場合、非零の項の係数は に関する最高次・最低次の項と係数を除いて の倍数である。

―――

「存在する」としたが、候補となる多項式を具体的に構成できる。記事(4)で行ったが、再度見る。例を挙げるのが早い。

『正多面体と素数』の計算をしましょう(5)―正二十面体と導手11の楕円曲線

shironetsu.hatenadiary.com

つづき。今回の記事は何だかよく分からないままに書く。

あるディオファントス方程式の解

V-座標系において、頂点・面・辺に対応する基本の正二十面体多項式は、
\begin{align}
V_{12}(x,y) &=
x^{11}y - xy^{11}
+11\,x^{6}y^{6},\\
V_{20}(x,y) &=
x^{20} + y^{20}
-2^2 \!\cdot\! 3 \!\cdot\! 19\left(x^{15}y^{5} - x^{5}y^{15}\right)
+2 \!\cdot\! 13 \!\cdot\! 19\,x^{10}y^{10},\\
V_{30}(x,y) &=
x^{30} + y^{30}
+2 \!\cdot\! 3^2 \!\cdot\! 29\left(x^{25}y^{5} - x^{5}y^{25}\right)
-3 \!\cdot\! 5 \!\cdot\! 23 \!\cdot\! 29\left(x^{20}y^{10} + x^{10}y^{20}\right)
\end{align}
であった。同じ記号を使って の一変数関数を定義する。
\begin{align}
V_{12}(X) &= V_{12}(X,1),\\
V_{20}(X) &= V_{20}(X,1),\\
V_{30}(X) &= V_{30}(X,1)
\end{align}
これらの間に
\begin{align}
V_{20}^3 - V_{30}^2 = -1728V_{12}^5
\end{align}
の関係があることは既に見てきた。興味深いのは、三つとも の整数係数の多項式であるため、
\begin{align}
A^3-B^2=-1728C^5
\end{align}
の整数解の無限系列を得られるということだ。試しに を代入してみる。
\begin{align}
V_{12}(1) &= 11,\\
V_{20}(1) &= 496 = 2^4\cdot 31,\\
V_{30}(1) &= -20008 = -2^3\cdot 41\cdot 61,\\
496^3 - (-20008)^2 &= -1728\cdot 11^5 = -278296128.
\end{align}
なるほど確かに解になっている。ところでこの整数たち、どうにも見覚えがある*1。

―――――

ここだ。Sageの楕円曲線に関するドキュメントの一節に496と20008が現れている。

Figure 1. Sageドキュメント " Elliptic curves over a general ring" のページ。

www2.math.ritsumei.ac.jp

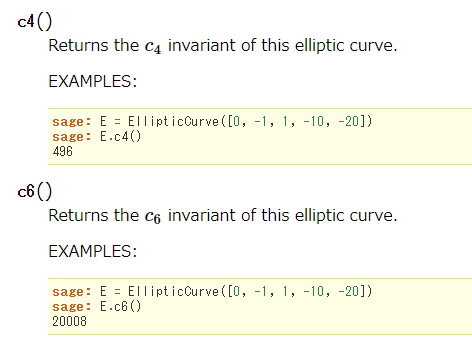
いったいこれは何なのだろう。

*1:496は完全数でもある

『正多面体と素数』の計算をしましょう(4)―正二十面体・あいだの次数・p=59問題

shironetsu.hatenadiary.com

つづき。今回の記事からは『正多面体と素数』に書かれていないことを調べていく。

ヒルベルト-ポアンカレ級数

一つ目の記事で概説したように、ヒルベルト-ポアンカレ級数は一次独立な正二十面体多項式が各次数にいくつあるかを教えてくれる。

改めて、
\begin{align}
P(t)
= \frac{1-t^{30}}{(1-t^6)(1-t^{10})(1-t^{15})}
= \sum_{i=0}^\infty d_i t^i
\end{align}
とおこう。 が次数 の一次独立な正二十面体多項式の個数になる。最初のいくつかの項は、
\begin{align}
P(t) =& 1+{{t}^{6}}+{{t}^{10}}+{{t}^{12}}+{{t}^{15}}+{{t}^{16}}+{{t}^{18}}+{{t}^{20}}+{{t}^{21}}+{{t}^{22}}+{{t}^{24}}+{{t}^{25}}\\
&+{{t}^{26}}+{{t}^{27}}+{{t}^{28}}+2 {{t}^{30}}+{{t}^{31}}+t^{32}+t^{33}+t^{34}+t^{35}+2t^{36}+\cdots
\end{align}
であって、 がそれぞれ頂点、面、辺に対する正二十面体多項式 に対応する。 の形を見ると分かるように、 を の なる整数解の個数とすると、 である。これは高次の正二十面体多項式を作る方法を考えると理解できる。 の積をとると の形で 次数 の正二十面体多項式が作られるが、 の間にはひとつの一次の関係式があるため、そのぶん独立なものが減る、ということだ。

『正多面体と素数』の計算をしましょう(3)―正二十面体・頂点を∞へ立体射影

shironetsu.hatenadiary.com

つづき。今回は立体射影で無限遠点へ写されるのが正二十面体の頂点の一つであるような座標系、V-座標系を考える。『正多面体と素数』の10.2.2節に対応。

『正20面体と5次方程式』を著したF. クライン［Klein-1，Klein-2］や、グレッグ・イーガン［Egan］もこの座標系を採用している。若干の記号の違いはあるが、前者ではここで計算するのと等価な式を見つけることができる。

この座標系を利用して計算を行うことの利点は明白で、 軸が5回対称軸になるため正二十面体多項式の項数が最少になるのだ。正20面体ではこれが最大の対称性（含まれる元の位数の最大値）なので、係数の観察が主眼でなければこれは大変良い性質だ。 軸回りの回転周期が短いためGIFアニメーションを作るときのレンダー時間が最も少なくなるという現代的な利点もある。

計算手順などは前の2つの記事で説明した通り。どんどん計算していこう。

『正多面体と素数』の計算をしましょう(2)―正二十面体・面の中心を∞へ立体射影

shironetsu.hatenadiary.com

つづき。今回は『正多面体と素数』10.2.3「面の中心を へ立体射影する場合」に対応。

上で半径1の球に外接する正20面体に対して、頂点・面の中心・辺の中点の座標が全て代数的整数になるような置き方が3つ考えられるのだった。
前の記事でそれぞれ以下のように名付け、E-座標系については既に扱った。

立体射影で無限遠点 ∞ に移る点	本記事での呼称
頂点	V-座標系
中心から外接球への面の中心の射影	F-座標系
中心から外接球への辺の中点の射影	E-座標系

今回の記事ではF-座標系を扱う。無限遠点に射影されるのは正確には「外接球の中心から面の中心（重心）の、球面上への射影」だが、混同がない限り単に「面の中心」と呼ぶことにする。球面上に張り付くまで膨らませた正20面体を考えると思えばいい。

計算の手順は前と同じ。振り返っておこう。

(1)　正二十面体の12個の頂点の座標を列挙する。
(2)　(1)で得た頂点たちの、立体射影による上への像を計算する。
(3)　(2)で得た12個の複素数を根に持つモニック多項式 を計算する。これが頂点に対する正二十面体多項式。
(4)　 を12次の2変数同次多項式 へ変換する。
(5)　 のヘッシアンの行列式（2変数20次の同次多項式）を の最高次の係数が1になるように定数倍して を求める。 は面に対する正二十面体多項式に一致する。
(6)　 と の関数行列式（2変数30次の同時多項式）を の最高次の係数が1になるように定数倍して を求める。 は辺に対する正二十面体多項式に一致する。
(7)　 を計算する。ただし 。

『正多面体と素数』の計算をしましょう(1) ――正二十面体・辺の中点を∞へ立体射影

これは何

橋本義武『正多面体と素数』（2020年、放送大学教育振興会）、主に10章「正20面体多項式」の計算を確かめます。

Sagemath等による計算ノートやその他のリソースを以下のリポジトリに上げています。順次追加予定。
github.com

その12番目のほとんど想像を絶する効用

黄金比 とは、 のふたつの実根のうち大きいほうのことをいう。すなわち、
\begin{align}
\phi=\frac{1+\sqrt{5}}{2}.
\end{align}
もう一方の解は

15世紀イタリアの芸術家にして数学者、フランシスコ会修道士のルカ・パチョーリはその著書『神聖な比例』（Divina proportione）の中で、黄金比の「その12番目のほとんど想像を絶する効用」として、黄金比を用いた正二十面体の構成法に言及しているという[Coxeter]。

その12番目の効用とはこうだ；縦横比を とする長方形を図1.のように組み合わせる。するとその頂点の全体が正20面体をなす。

縦横比Φ:1の長方形3枚をたがいに直交するように組み合わせる。頂点を結ぶと正20面体が現れる。

デカルト座標で表すと、複号は全ての組み合わせに渡るとして
\begin{align}
(0,\pm\phi,\pm1),\\
(\pm 1, 0, \pm\phi),\\
(\pm\phi, \pm 1, 0)
\end{align}
の12点が正20面体の頂点になるということ。

これから正二十面体を表現するために3つの座標のとりかたを見ていくが、辺の中点のうち6つが 軸上にくるこの取り方はとりわけ重要な意味を持つ。