Shironetsu Blog

@shironetsuのブログ

高坂海美呼称表手作り体験記

ミリオンライブ！

f:id:shironetsu:20180313184340j:plain:w400

　グリー版ミリオンライブ終了まで1週間を切った。悲しい。「思い出」にアクセスできる今しかできないことをやっておきたくて、高坂海美さんの他の人々に対する呼び名をまとめることにした。呼称表なんて太古から作られてきているものがインターネット上でいくらでも見られるけれど、ソースに直接あたることができるのはこの残されたわずかな期間だけ。自力でやってみたかった（ついでにスクショ作業の大変さを知っておきたかった）。下のほうに参考画像。

  • 五十音順。参考のため、年上 : >、同い年 : =、年下 : < の記号を付記。
  • 詳しくは下のほうに書いているが、ミリシタ及びコミカライズ「Blooming Clover」ソースも混在している。表中では括弧で注意を促す。特に注記の無いものはグリー版。
  • 2020年1月20日更新。本記事の作成は上述の通りグリー版ミリオンライブ終了前の2018年3月13日だが、それ以降も随時追加している。
  • ※印付きは自分では確認できなかったソースに基づくもの。
名前 年齢 呼び 呼ばれ
青羽美咲 20> 美咲ちゃん ？
秋月律子 19> 律子さん 海美※
天海春香 17> 春香さん 海美ちゃん
伊吹翼 14< バサバサ 海美さん
エミリー 13< えみりん（ミリシタ） 海美さん（ミリシタ）
大神環 12< 環 うみみ
春日未来 14< みらいっち 海美さん
我那覇響 16= 響 海美
菊池真 17> まこっちゃん 海美※
如月千早 16= 千早さん 高坂さん
北上麗花 20> 麗花 海美ちゃん
北沢志保 14< しほりん 海美さん
木下ひなた 14< ひなぴー（追記参照） 海美さん
高坂海美 16= 私（うみみ、うみみん） ／
桜守歌織 23> かおにゃん（ミリシタ） ？
佐竹美奈子 18> 美奈子先生・みなちん（ミリシタ） 海美ちゃん
四条貴音 18> 貴音さん 海美
篠宮可憐 16= 可憐 海美ちゃん
島原エレナ 17> えれなん ウミ
ジュリア 16= ジュリア 海美
白石紬 17> ？ ？
周防桃子 11< ももちん 海美さん
高槻やよい 14< やよちゃん 海美さん
高山紗代子 17> さよちん 海美
田中琴葉 18> 琴葉 海美ちゃん
天空橋朋花 15> 朋花様 海美さん
徳川まつり 19> まつりん 海美ちゃん （ウミミ姫）※
所恵美 16= めぐみー 海美・うみみん(ミリシタオフショット)
豊川風花 22> ふーちゃん 海美ちゃん
中谷育 10< 育りん 海美さん （海美お姉ちゃん（ミリオン女学園））
永吉昴 15< すばるん 海美
七尾百合子 15< ゆりりん 海美さん
二階堂千鶴 21> ちづるん 海美
野々原茜 16= 茜っち ウミミン
萩原雪歩 17> 雪歩さん 海美ちゃん※
箱崎星梨花 13< せりりん(BC) 海美さん
馬場このみ 24> このみちゃん 海美ちゃん
福田のり子 18> のりさん 海美
双海亜美 13< 亜美 うみみん
双海真美 13< 真美 うみみん
星井美希 15< ミキミキ 海美※
舞浜歩 19> 歩 海美
真壁瑞希 17> みずきん 高坂さん
松田亜利沙 16= ありりん 海美ちゃん
三浦あずさ 21> ？ 海美ちゃん※
水瀬伊織 15< いおりん 海美
宮尾美也 17> 美也・（美也ちゃん） 海美ちゃん
最上静香 14< モガミン 海美さん
望月杏奈 14< もっちー 海美さん
百瀬莉緒 23> 莉緒ねぇ 海美ちゃん
矢吹可奈 14< かなりん(ミリシタ) 海美ちゃん(ミリシタ)
横山奈緒 17> なおー(ミリシタ) 海美
ロコ 15< ロコロコ ウミ

　海美の付けるあだ名がかなり不規則なのは認識していたものの、改めて調べると本当に複雑。あだ名は本名に「りん」を付けるパターンだけではないし、本名で呼ぶ場合も「さん」「ちゃん」の付け方（または付けないか）が年齢の上下だけからは決まらない。高坂海美研究者はこの背後にある法則を見つけているのだろうか*1。ただ、特定の相手に対しては特に理由がない限り*2一貫したあだ名で呼ぶため、彼女なりのルールがあるのだろう*3*4。

　印象的なところでは、豊川風花を「ふーちゃん」と呼んでいるのがかわいい。少し年上の親戚のお姉さんくらいの気持ちで接しているのを想像。馬場このみを「このみちゃん」と呼んでいるのも全く純粋な感覚からそうしていそうで良い。同じく大人組の二階堂千鶴・百瀬莉緒は「女子力」の手本として慕っているところがあってまた良い。
　
　意外だったのが、グリー版では箱崎星梨花の名前を呼んでいる場面が見つからなかったこと。Blooming Cloverではあんなに一緒にいるのに。他にエミリー・スチュアート、木下ひなた、佐竹美奈子（追記参照）の呼び名が分からない*5。三浦あずさは「ミリオン女学園」で「あずさお姉さま」、「アイドルヒーローズ」で「あずささん」と呼んでいるが、素の状態での呼び名ははっきりしない。横山奈緒はミリシタのPBAコミュ第4話から（グリー版にもある？）。宮尾美也の呼び方には「美也」「美也ちゃん」で揺れがあった（ただしミリシタ以降は「美也」のみ）。

　桜守歌織と白石紬の呼び名はまだ分からない。中の人の上田麗奈さんと南早紀さんが事務所の先輩後輩ということで、白石紬さんとはMEG@TON VOICE!で小芝居みたいなことをやっていた気もするけど記録を残していないし特に台本の無い即興芸だったはず。

　これをまとめている最中、ミリシタに高坂海美中心のメインコミュ18話「ひろがる気持ち☆」が追加された。ココロ☆エクササイズ。あの世界一かわいいファイティングポーズがたくさん見られる。

（3/14追記）　
アイドル呼称一覧 - ミリオンライブWiki
　ミリオンライブwikiの呼称表。佐竹美奈子は「美奈子先生」らしい。2015年の誕生日のやりとりから。
高坂海美 - ミリオンライブWiki
　これ以外の空欄箇所は自分が作成したものと同じ。最上静香の欄の「静香ちゃん」が気になる。

　木下ひなたについては @superfroggest さんから「木下ひなたwiki」の呼称一覧を教えていただいた。
呼称表 - 木下ひなたwiki
　「ひなぴー」らしい。亜美真美と同じ。ただしソースは3周年記念ドラマCD*6だそうで、自力で確認ができない。

　エミリー・スチュアートについては未だ分からず。「えみりん」がしっくりくるけど案外「エミリー」そのままかも。バレエと日本舞踊という伝統舞踊を習っていた点での共通点があったりするのでそのうち絡んではくれそう。ミリシタでの属性も同じPrincessなのでそう遠くはないかも。

　とか言っていたらこんな会話があったことに気付いた。

f:id:shironetsu:20180318163137j:plain:w300

　プロデューサーの「苦手なダンスは？」という問いに対して「動きがゆっくりだから！私、落ち着いてるのって苦手だしね☆」とのこと（ネクストプロローグ編Lv2）
「バレエなら次のステップとか、姿勢を維持するのに集中しちゃってるけど…。ま、やってみたら違うかもしれないから、わからないけどねーっ。」

　それにしても「ふーちゃん」かぁ……「ふーちゃん」……ちょっと甘えのある感じがなんとも愛おしい……。ゲーム内の絡みが予想外に多かったが、LIVE THE@TER FORWAD(LTF) 03 Starlight Melody「MC03～その頃舞台裏では」にも会話がある。「永遠の花」を歌うにあたってまだ不安の残る風花さんを「ふーちゃん、がんばってね！」と送り出す海美の優しい声……。そしてミリシタTHE@TER BOOST!「超ビーチバレー」で新入生役高坂海美、キング役豊川風花として共演が決まっていることを思い出して動揺した。ミリシタで「ふーちゃん」を聞ける日も遠くない。
（3/14追記終わり）

（3/16追記）　センパイが来てくれない。
　昨日のミリシタのアップデートで過去のホワイトボードが見られるようになったので眺めていたら、中谷育の誕生日のホワイトボードに海美が書き込んでいたことを思い出した。

佐竹美奈子・中谷育（ミリシタ2017/12/16中谷育誕生日ホワイトボード）
f:id:shironetsu:20180316034703j:plain:w300

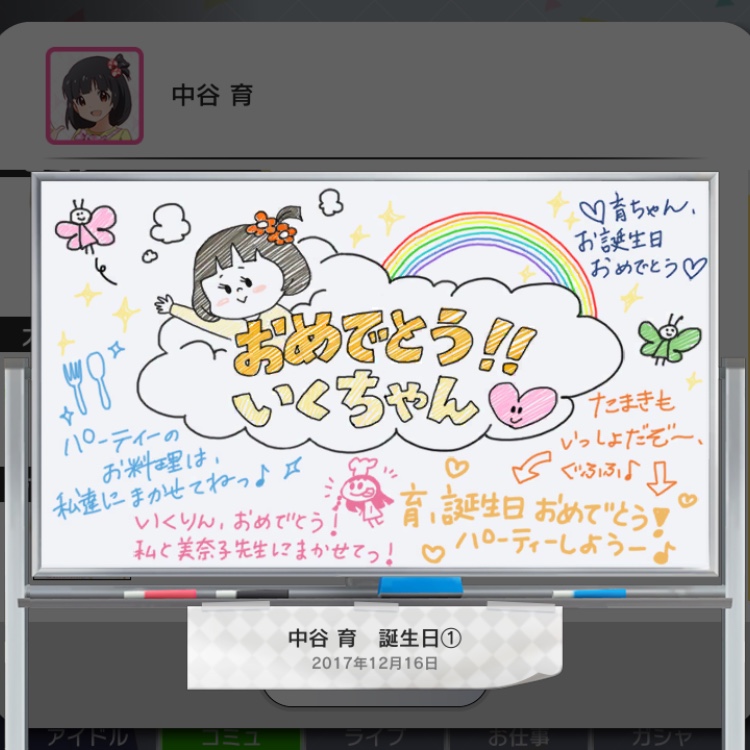
　自画像が可愛すぎる。それはともかくここでも佐竹美奈子のことを「美奈子先生」と呼んでいたので画像を追加。
　しかしこの「美奈子先生」呼びは背景にある色々があまりに魅力的ですね。厨房で手際よく料理を作る美奈子をキラキラした尊敬の眼差しで見ているんだろうな～とか。
（3/16追記終わり）

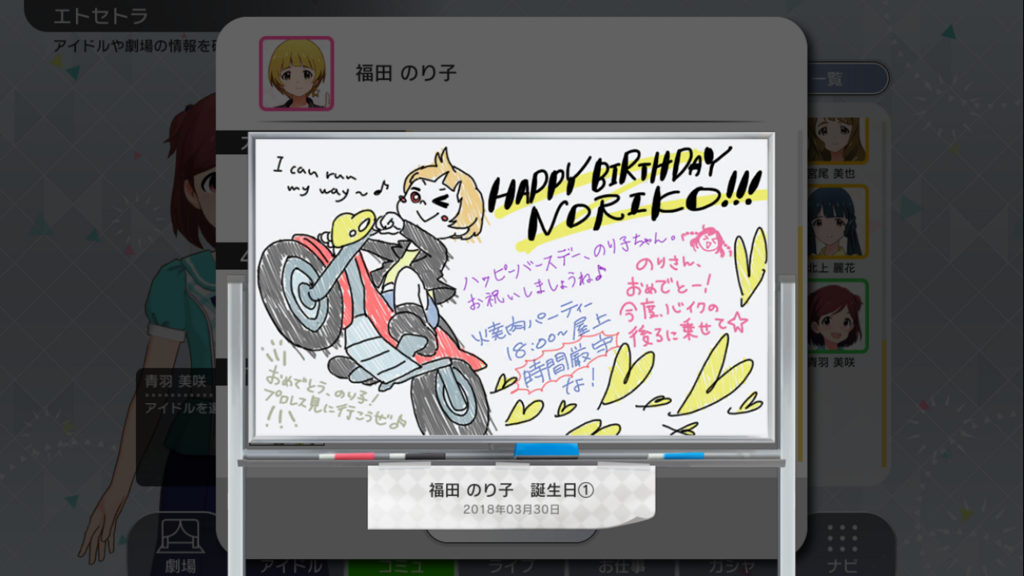
（3/30追記）　福田のり子さんお誕生日おめでとうございます。
　f:id:shironetsu:20180330080036p:plain:w400
　むむ…「のり子さん」…これからミリシタでもまたあだ名で呼ぶ仲になるのかどうか。

と、この記事を見直していたら桜守歌織さんを「香織」と書いていて泡を吹いた（修正済）。いちばんやっちゃいけないやつだぞ。
（3/30追記終わり）

（6/9追記）
　人生って楽しいーー！！！
5thライブで発表された閃光☆HANABI団（高山紗代子・高坂海美・佐竹美奈子・横山奈緒・福田のり子）、他の4人全員を海美はあだ名で呼ぶ。「美奈子先生」を聞けるか…！見るからに熱い面々（脳筋プリンセス……）なので今から楽しみ。超ビーチバレーも。人生って楽しい～～～～～
　ところで上に書いた「のり子さん」はいつかの時点で修正されていたらしい。よかったよかった。
f:id:shironetsu:20180609203345p:plain:w600
　ミリシタといえばメインコミュ20話の「朋花様」でざわついていたのも記憶に新しい。
f:id:shironetsu:20180609203756p:plain:w600
（6/9追記終わり）

（6/16追記）
　「呼ばれ方」を追加。最初の作成時にある程度はまとめていたものの、「呼び名」に比べると確認する範囲がどうしても多くなってしまって書けなかった。しかしどうせ「呼称表」とするなら双方向にすべきだろうと今更ながらに思い立ち……。※付きはアイドル呼称一覧 - ミリオンライブWikiからの引用。その他はソース画像が無いが、ほとんど「呼び名」が分かる場面のすぐ近くの会話中に出てきた。「呼び名」に比べるとトリッキーなところは少ないが、

  • 日常的に「うみみ」/「うみみん」/「ウミミン」と呼ぶのは大神環/双海姉妹/野々原茜さん だけ
  • のはずだがミリシタの「オフショット」で所恵美が「うみみん」と呼んだりしている
  • 矢吹可奈が年上を直接「ちゃん」付けで呼ぶのは比較的珍しい（他に七尾百合子・ロコ）

あたりは特筆。
（6/16追記終わり）

（6/21追記）折よく佐竹さんSSRをお迎えできました。
　閃光☆HANABI団イベントが始まりましたね。1万ptまで走りぬけてイベントコミュを見ました。
f:id:shironetsu:20180621012907p:plain:w600
（イベントコミュ第2話「ドドンとレッスン開始！」）
　うおーー……。
（6/21追記終わり）

（7/8追記）アキバの閃光☆HANABI団グッズを買えなかった
f:id:shironetsu:20180708225207p:plain:w600
（イベントコミュエピローグ「エンドレスなサマー」）
　やったーー！！

　………「ふーちゃん」に至るまでのやつもやってほしい………。
（7/8追記終わり）

（2019/01/30追記）
　年が明けて1月29日に更新された大神環メインコミュ「ヒーローで、アイドル！」にて歌織さんを「かおにゃん」と呼んでいることが判明。
「-にゃん」を付けるパターンのあだ名は他にいなかったのでまた不規則度が上がる。呼び名一つで「どう接しているか」の見え方が変わるので味わい深い。
　それにしても海美が虫のことを嫌っていなくて安堵した……。ずっとそのまま、たとえば野山に出かけたとき見つけた珍しい虫に目を輝かせていてね……。

f:id:shironetsu:20190309085428j:plain:w600

（2019/03/06追記）
　限定SSR「ガールズ・フェスティバル」のコミュにて「美咲ちゃん」を確認。青羽美咲→高坂海美はまず間違いなく「海美ちゃん」だが確実なソースを見つけられなかったため一応空欄。なお本名+ちゃんのパターンはこのみさんに続いて2例目。

f:id:shironetsu:20190306011557j:plain:w600

　そろそろこの記事を書いてから1年になるが、自分の知る限りこの間エミリーとは絡まなかった。十二単を着るというニアミス（？）が惜しい。

（2020/01/20追記）
　元号が変わり、年が明け、ついにミリシタのオファーテキストによってエミリーの項が埋まる。「えみりん」だった。予想通り。

f:id:shironetsu:20200120232248p:plain:w600

　紬の名前を呼ぶイベントはなかなか発生しない（見落としていなければ…）。しかしオファーテキストは定期的に追加されているため、コンプリートの希望が見えてきた。

　なお、これを書いているときには既に2枚目の限定SSR「新春ハピネスガール」の期間が終わっているが、うちのシアターには来なかった。無念。入れ替わりに「百花は月下に散りぬるを」イベントが開催されている。


　☆以下ソース画像。

*1:あだ名に関しては亜美真美・茜ちゃんと一部重複してはいる

*2:佐竹美奈子に対しては、みなちん=>美奈子先生という変化が閃光☆HANABI団イベントコミュで起こっている。

*3:メタ的にはシナリオ作成上の都合がもちろんあるだろうけれど…。

*4:なお、「アイドルヒーローズ」で役を演じているときには本名（主に下の名前）で呼ぶ。

*5:本記事作成時

*6:BLOG│THE IDOLM@STER OFFICIAL WEB | バンダイナムコエンターテインメント公式サイト 応募者全員が貰えたそうだがその頃自分は初めてまもなかった…

続きを読む

「昏き星、遠い月」CDを聞いたあと

ミリオンライブ！

f:id:shironetsu:20180228183157p:plain

　MTG05の「昏き星、遠い月」ドラマパートを聞きました。練習風景が描かれたイベントストーリー中で断片的に演じられた劇を補間する内容。台詞がより充実するとともに曖昧だった点のいくつかが解消された。ただしどういう理由か練習時との相違もあってやや慎重に読む必要がある。

コミュ6話視聴後の記事
shironetsu.hatenadiary.com

フラゲ前の記事
shironetsu.hatenadiary.com

　場面ごとに大雑把にメモ。

  • 『Prelude』

　最初のクリスティーナが語るバックに流れる音楽、エコーのかかった声が劇場を思わせて良い。エドガーが「すっかり寒くなってきた」と言っているので二人の出会いはそういう時季らしい。ついでにクリスティーナは日傘をさしている。
　そしてさっそくここでイベントストーリーとの相違が生じている。あちらではヴァンパイアに襲われた死体を見つけたエドガーが、路地裏に佇むクリスティーナに声をかけたことが二人の出会いのきっかけだった。一方こちらでは仕事を終えたエドガーが平凡な一日の終わりに見つけている。イベントストーリーではぼかされていたクリスティーナの狩りの様子も直接描かれずいぶん簡単になった。

  • 『再会、強襲』

　再びエドガーの前に姿を現すクリスティーナ。からかいからかわれる様子がかわいい。全体的に儚げな雰囲気をまとっていたイベントストーリーのクリスティーナにくらべてお茶目。
　後半ではアレクサンドラたち一家の暮らしていた屋敷が襲われたときのことが語られる。エレオノーラが犯人ではない可能性を考えたりもしたがさすがにそれはなさそうだ。そしてアレクサンドラは「不浄を祓う剣の使い手」だとエレオノーラの口から語られる。……悩ましい。
　エレオノーラ（と辺境伯）が屋敷を訪問したのは何のためだったか。香を携帯していたのだから誰かをヴァンパイアに変える準備は常にできていたのだろうけれど、予め目的としていたわけではないのかもしれない。「不浄を祓う剣の使い手」の噂を聞いて手元に置くために父母を殺し、偶然見つけたノエルをヴァンパイアに変えて人質に取った……といったあたりか。

  • 『大切なもの』

　クリスティーナがエドガーは女だと知ったきっかけが「偶然知ってしまった」になっている！イベントストーリーでは倒れたエドガーを家に連れ帰ったときに知ったことになっていた。そこで互いの秘密を打ち明け合って結びつきを強める……という意味があったはずだったが。クリスティーナが男だと触れられないことより、この違いのほうが重大かもしれない。エドガーの男装の理由（第2話の台詞「あんな場所じゃ、女は生きていけないから……」）についてもこちらでは特に語られない。
　二人が追剥ぎに襲われる場面が続く。永吉昴演じる不良に「ルカ」という名前が付いていて、エドガーと知り合いだったことが分かるやりとりがある。クリスティーナに締め付けられて苦しむ声の演技がとても良い。

  • 『誇り』

　前半はイベントストーリー第6話に含まれる内容とだいたい同じ。ただエドガーがアレクサンドラとナイフでやりあう場面が加わり、ミリシタのMVにより近くなっている。
　城に帰ったアレクサンドラが正体をさらしたエレオノーラに切りかかる場面。やはり油断というか、アレクサンドラはヴァンパイアになる道を選ぶと疑っていなかったことが死に繋がっている。切り付けられたときの当惑。「ああ……そう……アレクサンドラ……あなたは……。そうだったの？……知らなかったわ……。」この台詞は語られてない設定があるというよりは、自分がヴァンパイアになったときの迷いのない選択と比べているのだと考えたい。実際、姉妹がこれ以上の不幸を味わわないためにはアレクサンドラがヴァンパイアになるしかなかったはずで……。

  • 『ひかりさす』

　エレオノーラが人間だったときのことが初めて語られる。「この城は呪われている、ヴァンパイアがいる」と叫ぶ暴徒。その人間たちに殺された元夫と娘のアンジェラ。逃げ出した彼女の前に現れた一人のヴァンパイア（「彼」）。「復讐したいか？」と聞かれて迷うことなくヴァンパイアとして生きていくことを選ぶエレオノーラ。「虚ろな世界、壊してしまって…創り直すの」という歌詞の背景にあるのは彼女の深い絶望か。

  • 『Overture』

　preludeとovertureはどちらもだいたい「始まりの曲」の意味でいまひとつ違いが分からなかったが、インターネット上にはこの疑問に対する回答が無数に存在して、それによるとovertureはその後のオペラのあらすじのような内容を含む音楽である一方、preludeはもっと広く開幕に合わせて演奏される楽曲らしい。具体例を知らないので曖昧だけど。「昏き星、遠い月」がoverture的な楽曲ということになる？

overture : 序曲 - Wikipedia
prelude : 前奏曲 - Wikipedia

　エレオノーラが言ったようにノエルがヴァンパイアとして覚醒する凶兆を見せてこの物語の幕は下りる。こちらでははっきりとは言っていなかったが、アレクサンドラはノエルが人を襲うようになれば殺す決意を持って旅に出たはず。姉妹の旅はどこで終わるのだろう。


　考察。さて、イベントストーリーとの一番大きな相違点はクリスティーナが男であると直接的な言及がないことだろう。加えてクリスティーナの「罪」にも直接触れられていない。とはいえそれらの設定が消えてしまったと考えるともはや別作品、可能な限りどちらも採り入れる立場で*1。
　「昏き星、遠い月」のラストに語られる「愛し子」を重視してCD購入以前に検討していた、クリスティーナがエレオノーラの実子であったりエレオノーラが人間であったりする可能性はもうほとんど消えたといっていい。新たに浮かんでくるのは娘のアンジェラが実は生き残っていてエドガーとして育った……といった可能性。
　「腐った世界」から逃げ出して理想郷を探すのがエドガー、壊して作り直そうとするのがエレオノーラ。エドガーの誘いに乗るのがクリスティーナ、エレオノーラの甘言を拒んだのがアレクサンドラ。「黒」側と「白」側（舞台衣装）にそういった対比はあるものの、エドガーとエレオノーラを血縁関係で結ぶべき理由としては薄い。やはりアンジェラは本当に幼くして死んでしまったと考えるのが妥当か。
　主要人物4人の関係については、今のところどの2人の間にも血縁関係を仮定することに合理的な理由はないと思う。

　しかしエレオノーラとクリスティーナの関係がなおも問題であることに変わりはない。エレオノーラの前に現れたのは男のヴァンパイアらしいので即座に「クリスティーナがエレオノーラをヴァンパイアに変えた」説の補強になると考えた。
　しかしエレオノーラが人間だったころの城にヴァンパイアがいるという噂が立ったのは何が原因だったか。その後に現れたヴァンパイアとの関係は？
　エレオノーラの正体をクリスティーナが知っている理由としてこれを採り続けるためには、同時に説明すべきことがちょっと多すぎる。

　点と点を無理やり繋いで新しく次の説を立てる。

　エレオノーラを見そめた男のヴァンパイアが民衆を扇動して彼女の城を襲わせる。「あの城にはヴァンパイアがいる。」愛する娘と夫を失いながら、命からがら逃げだしたエレオノーラの前にそのヴァンパイアが現れ、ヴァンパイアになって人間たちに復讐するという道を示す。「復讐したいか？」他の選択肢は考えられなかった。そうして一人のヴァンパイアが生まれる。

　時が経ち、あの日の悲劇がその男の仕組んだものだったと知ったエレオノーラは、彼を殺して復讐を果たすと同時に、全ての悪しきヴァンパイアを滅ぼすことを誓う。単身ヴァンパイアを殺しながら、更に力を蓄えるため軍を従える辺境伯に取り入る。そして噂に聞く「不浄を祓う剣の使い手」を側に置くためアレクサンドラ一家の屋敷を襲う。

　さらに月日が流れ、あるとき国王から辺境伯へヴァンパイア討滅の勅令が下る。辺境伯夫人エレオノーラは街に侵入したらしいヴァンパイアの捜索と退治をアレクサンドラに命じる。しかしそのヴァンパイア、クリスティーナの目的はエレオノーラに殺された同族たちのための復讐だった。二度目の接触でクリスティーナはアレクサンドラにエレオノーラの秘密を教える。クリスティーナが目論んだ通り、アレクサンドラはエレオノーラを殺す。

　エレオノーラにとって、アレクサンドラがヴァンパイアとして生きることを拒むなど予想もしていないことだった。ヴァンパイアになれば愛する妹と永遠に生きていくことができるのに。自分がかつてそうしたように。

　……この説だとクリスティーナが男であってもなくても変わりがないかも。しかしエレオノーラの城がよりによって「ヴァンパイアがいる」という噂のために襲われた事件と、その直後にヴァンパイアが現れた理由の関係を無理なく繋ぐにはこれくらいしか考えられない。いっそクリスティーナが男であるという設定が生きているとしても他の何にも関係していない、と考えたほうが楽。
　隠された出来事があるとすれば、人間を憎むべき過去を持つエレオノーラが「ヴァンパイアの淘汰」に心血を注ぐようになったきっかけだろう。強いヴァンパイアを集めてやがて人間たちの世界を壊そうとしていた？　軍を従えたり（アレクサンドラは「辺境伯夫人の軍」という言葉を口にしている）、祓魔の騎士：アレクサンドラを獲得したのは「復讐」が原動力になっていることは間違いないと思う。しかし何に対して？


　難しい。まあ答えがすべて明白になってしまわず、語れる部分が残されているので良かった。たぶんまだ何か思いつくたびに追記していく。


　……ところでちょうど一か月後の3月28日はMTG06"Cleasky"のCDの発売日。そのドラマパートは「昏き星、遠い月」より分量が多いという朗報がある（dareradi第89回の角元さんの発言）。オープニング曲としての「虹色letters」はこのストーリーによって完成するものであるはず。「未送信letter」と二人の手にある手紙の間を繋ぐ出来事とは……。バレンタインの生放送でも二人して「エモい」と言っていたドラマCD、「昏き星、遠い月」を聞いた後では更に期待が高まる。

www.youtube.com
あまりにもいい……二人の優しい声に切なげな笑顔、目を合わせるところとか「未送信letter」の手を繋いで歩くような振り付けとか……。


（3/3追記）
　製作者の意図がどうあれ、それが明らかにされない以上作品解釈に正解不正解は決められない（し相異なる解釈で楽しむべきだ）と思うけれど、イベントコミュとCDのボイスドラマはやはりある程度区別したほうがよさそうだという考えに傾きつつある。……端的に言うと、CDではクリスティーナが男だという設定は反映されていないのではないかと。多くの人にとっての困惑の種になっているのではないだろうか。

　この物語の登場人物たちそれぞれが秘密を抱えている、というのはストーリーの重要な要素だった。このことはイベント終了後に届いたメールでも千鶴さんが語っている。

　ところで、お気付きでして？
　『昏き星、遠い月』の登場人物達には、
　全員、秘密があったことに……。　

　クリスティーナは自分が男で、ヴァンパイアであること。そして「罪」。
　エドガーは自分が女であること。
　エレオノーラは自分がヴァンパイアであること（と過去？）。
　アレクサンドラは妹ノエルがヴァンパイアになったこと（それを妹に教えていないという秘密）。

　エドガーにとって、自分が女であることを知られるのは弱みを晒すようなことだった。それを本人の意図に反して知ってしまったかわりに、クリスティーナは自分が男であると明かした。しかしクリスティーナの秘密はそれひとつではない。もうひとつの秘密、自分がヴァンパイアであることはまだ隠していた。そして、自分がヴァンパイアの力を発揮する姿を見られたくなかったがためにエドガーは不良に襲われてしまう。

　イベントコミュでは互いの秘密を明かす場面は物語の進行上非常に重要だった。それに美しい。人間ひとりの生殺与奪を握るに十分な力をもつヴァンパイアの家で、性を偽ってまで強く生きようとする少女が介抱されている図。クリスティーナの住処でエドガーが目覚めて会話する場面、絶対に舞台で見たい……。

　一方CDではクリスティーナはエドガーが女であると「偶然知ってしまっ」ている。そう言われたあとのエドガーの反応もずいぶん軽い。CDとコミュは相補的で両方聞いて初めて全体像が分かるようになっている、という考えも否定しきれないとはいえ、そこまで慎重に組み立てているならこの重要なポイントを変えるのはちょっと変。そういった理由で、単に言及されていないのではなくCDのクリスティーナは男として設定されていないのではないかと疑ってしまう。

（また追記）
　（作り手の方々がニコ生やリスアニ！等でこの作品について語られるのを目にする機会が増えるにつれ、CDとゲームとで設定が異なると考える態度こそが不誠実に思われてくる）というか曲とシナリオ作りが同時に進行していたのは明らかなのでメタ的に見てもやはりクリスティーナは男だと考えたい。少なくとも秘密を明かすタイミングが異なっている点については別のルートが選ばれとみなせばいける。そういえばこの作品はそういう要素のあるゲームの作中作だった。アイドルマスターミリオンライブ！

*1:イベントストーリーだけをもとにして色々考えたように、このCDドラマだけを材料にして考察するのもありだと思うけど

「昏き星、遠い月」公演前の

ミリオンライブ！

　アイドルマスター ミリオンライブ！5周年おめでとうごさいます。

　"THE IDOLM@STER MILLION THEATER GENERATION 05 夜想令嬢 -GRAC&E NOCTURNE-"の発売日は明日2月28日。イベント終了から1か月と少し。長かった。「合言葉はスタートアップ！」、「Princess Be Ambitious!!」・MS06CD発売、田中琴葉さんの〈資料運び〉解放、「虹色letters」等この間に色々あった。
　フラゲの前に、前回の記事の後に考えたこと見たことなどを書き残しておく。CDのドラマパートで全ての答えが明確になるとは限らないものの、イベントストーリー+フルサイズしかない今*1想像していることのいくつかはきっと無に帰してしまうはずなので……。

前の記事の要点

shironetsu.hatenadiary.com
　追記部分以外はフル尺公開前のもの。「愛し子」を重視しない考察。永吉さんに頼まれてプロデューサーが死体役になるという一見ギャグっぽい場面が挟まれることで、不良ふたりを瞬殺したクリスティーナの強さから注意が逸らされるという仕掛けをいま一度味わってほしい……。この点に限らず全体的に叙述トリック的な面白みがあるのが良い。練習を眺めているプロデューサーとしての視点は本来筋書きを一番理解しているはずなので。
　前の記事の読みは「故意に言及しないこと」はあっても嘘は含まれないと考えている点でかなり素直。おおよそ次の推測が骨子。

  • クリスティーナがエレオノーラをヴァンパイアに変えた。クリスティーナの言う「罪」はこのこと。
  • クリスティーナは自分が生んだエレオノーラという怪物（同族を「淘汰」の名のもとに殺している）を討つためスラム街に潜伏していた。
  • エドガーによるアレクサンドラへの説得が功を奏し窮地を脱すると、彼女にエレオノーラの秘密を暴露することで殺害を教唆して遂に「罪」を清算した。

　
　クリスティーナとエレオノーラの関係はストーリー中で言及がないため諸々の描写から推察するしかない。はっきりしているのは「クリスティーナはエレオノーラの正体をアレクサンドラに教えた」ということだけ。エレオノーラの側がクリスティーナのことを知っているかどうかさえ明確ではない。そういった色々の断片的な要素がうまく整合する仮説として選んだのが「クリスティーナがエレオノーラをヴァンパイアに変えた」だった。今に至るまで特に反証も思いついていない（エレオノーラ側の感情が若干弱いかなという気はするが）。


「愛し子」

　イベント終了後先行配信された「昏き星、遠い月」フルバージョン。そのラストの「愛し子」を踏まえると先の説は、しかしなんとも弱い。

ねえ……とても愛していたわ……本当よ？……私の愛し子……。

　百瀬莉緒ーーーー！！！！！！！！昨日公開されたメインコミュ第17話見ましたか？……普段はあんな感じの気さくなお姉さんなのに……こんな息も絶え絶えの「悪女」が最期に思った誰にも届かない愛を迫真の演技で……
　さて。「愛し子」という語はストーリーコミュ中でも口にしている。ただしアレクサンドラの妹ノエルに対して。

f:id:shironetsu:20180227021620p:plain

　「まるで私の愛し子」という表現、これだけを聞いても実の娘ではないノエルに向ける言葉として不自然なところはないが、上の台詞を聞いた後では「本当の愛し子」がいる可能性を考慮に入れざるを得ない。　そのうえこういう話があった（コメントくれた方もありがとうございます）

マリア・エレオノーラ・フォン・ブランデンブルク - Wikipedia
クリスティーナ (スウェーデン女王) - Wikipedia
＞1636年、マリアは娘クリスティーナを監禁したが、のちにマリアは反逆の疑いをかけられてデンマークへ亡命し、王族としての特権を剥奪され、事実上スウェーデンから追放された。1643年にブランデンブルクへ渡った。
＞マリアは1648年に再びスウェーデンへ戻ったが、クリスティーナとの親子関係が修復することは二度となかった。

Leonora Christina Ulfeldt - Wikipedia
　ほぼ同時代の17世紀中ごろににデンマークでもレオノーラ・クリスティーナ・ウルフェルト*2も20余年に渡る幽閉生活をコペンハーゲン城の「青い塔」で送っている。母子関係が原因ではないけど。


　もちろん実在していた人物から名前を取っているのだとしても境遇を直接なぞっているはずはない。しかしこれを見ると、エレオノーラはクリスティーナの実子・監禁・逃亡・親子間の確執……などと想像を膨らませずにはいられない。

　そう思いながら再度ストーリーコミュを見ると、ヴァンパイアになったノエルを眠らせる香をエレオノーラが持っていた理由も違ってくる。元はクリスティーナを眠らせるために使っていた？　他のいくつかの要素も併せて次の説が立てられる。

　エレオノーラは実の子であるクリスティーナを香で眠らせながら長年監禁していた。しかしあるときクリスティーナは目覚め、逃亡して自由の身となった。ヴァンパイアとしての生を苦痛そのものと考えるエレオノーラは、クリスティーナの行方を捜し死をもって安らぎを与えようとする。
　数年後、配下のアレクサンドラはクリスティーナを探し当てるが、「エレオノーラの正体はヴァンパイアである」という秘密のみを携えて帰ってくる。秘密を知っているのはただひとりだったはず。「愛し子」クリスティーナは自らの正体を、ヴァンパイアを憎むアレクサンドラに教えた。アレクサンドラを通じて届いた、生きる決意と離別のメッセージ。母としての役割の終焉。我が子が死を拒んだ一方で、死を受け入れたエレオノーラはアレクサンドラに嘘の動機（弱いヴァンパイアの淘汰と王国の建設）を話しながら自分を殺すように仕向けた。アレクサンドラの一振りでエレオノーラは致命傷を負い、薄れゆく意識の中で思う。「ねえ……とても愛していたわ……本当よ？……私の愛し子……」

　エレオノーラが死を受け入れたと考える理由のひとつは、強力なはずの彼女が実戦経験に乏しいはずのアレクサンドラに抵抗しているように見えないから。しかしヴァンパイアはそもそも不死であるはず。この点から疑うこともできる。


エレオノーラの正体

　ヴァンパイアになると「二度と死ねなくなる」とはクリスティーナの台詞として歌詞にも含まれている。一方で血液を摂取しなければ死んでしまうともエドガーには話している。単純に考えれば寿命が無いかあるいは人間よりはるかに長い、つまり自死を選ぶ以外に死ぬ方法がないということだろう。だからエレオノーラが殺されてしまったことが直接ヴァンパイアであることを疑うべき理由にはならない。
　……とはいえエレオノーラが実はヴァンパイアでないという可能性には一考の余地がある。何せアレクサンドラとエレオノーラの会話以外にそうと分かる描写がない。そのうえアレクサンドラはヴァンパイアを見分けることができないと来ている。

f:id:shironetsu:20180227021732p:plain
（アレクサンドラがクリスティーナ・エドガーと出会った場面）

　そうなると死に際のエレオノーラの言葉の嘘をついていたと考えるべき部分が増える。大筋は上のままで、エレオノーラが人間であるとの説に基づくとこうなる；

　クリスティーナは母が全てを背負ってくれるだろうと確信して、実際には人間であるエレオノーラの正体がヴァンパイアであるとの嘘の秘密をアレクサンドラに教えた。我が子を愛するエレオノーラはアレクサンドラの言葉に合わせて自分がヴァンパイアを探す理由を偽った。同時に、アレクサンドラの父母を殺してノエルをヴァンパイアに変えたのは自分であるとも――実際にあの日屋敷を襲ったのはクリスティーナだったのに。真実は自分の死と共に葬られ、過去から切り離されたクリスティーナは自由になる。

　母子の心の読み合いが異常に高度になって良い。捩じれきった愛の形。ノエルをヴァンパイアに変えたことがクリスティーナの「罪」であるとの考えを以前は否定していたが、この説では少なくともそのひとつとして復活しうる。……まあちょっと無理がある感は否めない。
　

クリスティーナの罪

f:id:shironetsu:20180227021818p:plain

　クリスティーナの罪。結局何なのか？ この解釈によって可能性はもっと分岐しうる。事実としてエドガーと旅に出ることができない理由であった「罪」、クリスティーナにとってあの街に縛り付けていた軛であったわけだが、どのように縛り付けていたのか？

  • 「クリスティーナがエレオノーラをヴァンパイアに変えた」説……エレオノーラをヴァンパイアに変えたこと。彼女を討つための使命を果たすまで街を離れられない。
  • 「母エレオノーラが死を与えることで子クリスティーナを救おうとした」説……母から逃げたこと？命を狙われている以上エドガーを巻き添えにはできない。
  • 「エレオノーラは人間である」説……アレクサンドラ一家を襲ったこと？同上。

　瀕死のエドガーにここで死ぬかヴァンパイアになるか選択を迫る場面で苦しんでいることからは、人間を食糧とするしかないヴァンパイアとしての生そのものを罪だと考えているようにも見える。もしくは人間を殺さずにヴァンパイアに変えてしまうことか。考え始めるとどれもそれなりに魅力があって決定打となる証拠に欠ける。

　「罪」がどのような形で解消されたのであろうと（あるいは解消されたわけではないのだとしても）ヴァンパイアとしての空虚で孤独な生を送っていたクリスティーナがエドガーとの出会いによって変化したのは確か。

f:id:shironetsu:20180227021849p:plain

　この「少し変わった形のボーイ・ミーツ・ガール」の背景に何があるのか、間もなく始まる本公演：CDのドラマパートでどこまで明かされるか楽しみ。

www.lantis.jp

*1:先日2曲目の"Everlasting"が誤って配信されて取り逃されるということがありましたね。勢いで購入してしまったが結局聞いていない。

*2:ポール・アンダーソンによるハードSF『タウ・ゼロ』Tau Zeroの宇宙船Leonora Christineの由来らしい。エンジンが故障して故郷との相対速度が光速に近づいていくこの宇宙船の中に乗員たちは閉じ込められ、宇宙が年老いていく様子を目の当たりにする。読んで。

球面調和関数で正20面体をつくる(3) - l=28までの表

物理・数学

　球面調和関数でサッカーボールをつくる記事のつづき.
shironetsu.hatenadiary.com
shironetsu.hatenadiary.com

　改めて, 「{SO(3)}の{\ell}次の既約表現({(2\ell+1)}次元表現)の, 正20面体群{I}への制限を既約分解したときの恒等表現{A}の基底」を存在すれば{| \ell A \alpha\rangle}で表すことにする. {\alpha}は重複度に応じてつけるラベル. 一般に{|\ell A \alpha\rangle}は

{ |\ell A\alpha\rangle = \sum_{m=-\ell}^\ell Q_{\ell m\alpha} |\ell m\rangle\\ Q_{\ell m\alpha}\in\mathbb{R},\ \ \ \sum_{m=-\ell}^\ell Q_{\ell m\alpha}^2=1 }

で表せるが, 前回の記事でそうしたように{C_5}軸を{z}軸にとると{m\equiv 0\ {\rm mod}5}以外の係数はゼロになる. さらに{C_2}軸を{y}軸にとると,

{ Q_{\ell(-m)\alpha}=(-1)^{\ell+m}Q_{\ell m\alpha} }

になる(従って{\ell}が奇数のとき{m=0}の係数はゼロ).

そして, 少なくとも{\ell<29}では(重複度は1なので{\alpha}は省く)

{ Q_{\ell m}=\pm \sqrt{\frac{c_{\ell m}}{N_\ell}}\\ N_\ell\in\mathbb{N},\ \ \ c_{\ell m}\in\mathbb{N}_0,\ \ \ {\rm gcd}(N_\ell, c_{\ell m})=1 }

と, 既約分数の平方根になる. それらをまとめたのが下表.

その値は次のようにして得た:

(1){\ell=15}同士の積表現が{\ell=2,4,8,14}の基底を含まないことから{|15A\rangle}が決定される.
(2)同時に{\ell=30}以下の偶数次数の表現が得られる.
(3){\ell=12,15}の積表現から{\ell=21,25,27}(奇数次数)の基底が得られる*1

{Q}の符号は{c}のほうにつけている. たとえば, {N}の表から{N_{10}=3\cdot5^4}で, {c}の表での{\ell=10,m=5}の欄に"{-3\cdot11\cdot19}"とあるから,

{ Q_{10,5}=-\sqrt{\frac{c_{10,5}}{N_{10}}}=-\sqrt{\frac{3\cdot11\cdot19}{3\cdot5^4}}=-\frac{\sqrt{209}}{25} }
と読む.

{N_\ell}の表
{ \begin{array}{|c|c|c|c|c|c|c|c|c|}\hline \ell&0&6&10&12&15&16&18&20\\ \hline N_\ell&1 &5^2&3\cdot5^4 &5^5 &2^2\cdot5^5&2^2\cdot3\cdot5^7&5^7&5^9\\ \hline \end{array} }
{ \begin{array}{|c|c|c|c|c|c|c|c|}\hline \ell&21&22&24&25&26&27&28\\ \hline N_\ell &2\cdot5^7&2\cdot3\cdot5^{10}&5^{10}&2\cdot3\cdot5^{10} &2\cdot3\cdot5^{12} & 2^2\cdot3\cdot5^{10} & 2^2\cdot3\cdot5^{12}\\ \hline \end{array} }


{c_{\ell m}}の表
{ \begin{array}{|c|c|c|c|} \hline \ell\backslash m & 0 & 5 & 10 \\ \hline 0 & 1 & 0 & 0 \\ 6 & 11 & 7 & 0 \\ 10 & 13\cdot19 & -3\cdot11\cdot19 & 11\cdot17 \\ 12 & 3^2\cdot7\cdot17 & 2\cdot11\cdot13 & 3\cdot13\cdot19 \\ 15 & 0 & -5\cdot23\cdot29 & 2\cdot3\cdot11\cdot29 \\ 16 & 2^6\cdot5\cdot19\cdot31 & -3\cdot5\cdot13\cdot17\cdot31 & -2\cdot7\cdot17\cdot23\cdot31 \\ 18 &5\cdot11\cdot17\cdot23 & 2^3\cdot3^2\cdot5\cdot19 & 3\cdot7\cdot11\cdot19 \\ 20 & 5\cdot7\cdot23\cdot29 & -2\cdot11\cdot17\cdot19\cdot29 & 17\cdot19\cdot41^2 \\ 21 & 0 & -29\cdot31\cdot41 & -2^2\cdot13\cdot41\\ 22 & 2^2\cdot3\cdot5\cdot11\cdot19\cdot31\cdot37 & -7\cdot13\cdot23\cdot31\cdot37 & -2\cdot7\cdot17\cdot23\cdot29\cdot37 \\ 24 & 5\cdot7^2\cdot13\cdot23\cdot29 & 2^3\cdot3\cdot11\cdot59^2 & 2\cdot19^3\cdot31 \\ 25 & 0 & -7^2\cdot31\cdot37\cdot43& 2\cdot3\cdot7\cdot11\cdot19\cdot37\cdot43\\ 26 & 2^2\cdot3^3\cdot13\cdot29\cdot31\cdot41 & -5\cdot7\cdot11\cdot23^3\cdot41 & 2^7\cdot5\cdot7\cdot19\cdot23\cdot41 \\ 27 & 0 &-17\cdot19\cdot37\cdot41\cdot47& -2\cdot41^3\cdot47\\ 28 & 2^8\cdot3^2\cdot7\cdot31\cdot37\cdot43 & -5\cdot11\cdot13\cdot29\cdot37\cdot43 & -2\cdot3\cdot5\cdot13\cdot17\cdot23\cdot29\cdot43 \\ \hline \end{array} }
{ \begin{array}{|c|c|c|c|} \hline \ell\backslash m&15 & 20 & 25 \\ \hline 15 &7\cdot11\cdot13 & 0 & 0\\ 16 & 3^2\cdot17\cdot23\cdot29 & 0 & 0\\ 18 & 19\cdot29\cdot31 & 0 & 0 \\ 20 & -2^3\cdot11\cdot19\cdot31& 11\cdot13\cdot31\cdot37 & 0\\ 21 &3\cdot13\cdot17\cdot41 & 17\cdot19\cdot37 & 0\\ 22 & -23\cdot29\cdot103^2 & 13\cdot19\cdot23\cdot29\cdot41 & 0 \\ 24 & 2^2\cdot3^2\cdot11\cdot31\cdot37 & 31\cdot37\cdot41\cdot43 & 0\\ 25 & -7^2\cdot43\cdot61^2 & 3^2\cdot7^2\cdot11\cdot41 & 2\cdot5\cdot11\cdot23\cdot41\cdot47 \\ 26 & 3\cdot5\cdot23\cdot37\cdot139^2 & -5\cdot37\cdot43\cdot89^2 & 2\cdot7^2\cdot17\cdot37\cdot43\cdot47 \\ 27 & 2\cdot3\cdot17\cdot19\cdot47 & 2^6\cdot17\cdot19\cdot23\cdot43 & 5\cdot7\cdot13\cdot19\cdot23\cdot43\\ 28 & -2\cdot5\cdot23\cdot29^3\cdot41 & -2^3\cdot3^2\cdot5\cdot13\cdot29\cdot41\cdot47 & 7\cdot17\cdot29\cdot41\cdot47\cdot53 \\ \hline \end{array} }

　せっかくなので球面調和関数の重ね合わせとして視覚化しておく.
{\ell=25}
f:id:shironetsu:20180220215132g:plain:w500

{\ell=27}
f:id:shironetsu:20180220215222g:plain:w500

{\ell=28}
f:id:shironetsu:20180220215314g:plain:w500

　表を観察して気になること.
　まずこの範囲で{N_\ell}は2,3,5しか因数に持たない. 理由が分からない.
{c_\ell}の因数も小さい素数ばかり並んでいる. 今の構成法ではこれは自明ではない. 単に直和分解するだけなら, 3j記号の閉じた形を考えると大きな素数は出てこないが, 今は規格化も含んでいるため.つまり和が{N_\ell}である. たとえば,{\ell=24}の欄から
{ (5\cdot7^2\cdot13\cdot23\cdot29)+2\cdot(2^3\cdot3\cdot11\cdot59^2)\\ +2\cdot(2\cdot19^3\cdot31)+2\cdot(2^2\cdot3^2\cdot11\cdot31\cdot37)+ 2\cdot(31\cdot37\cdot41\cdot43)=5^{10} }
が分かる*2. 大げさかもしれないが数論的にはどう解釈すべきなのだろう.

　以前の記事で見た限り, {x,y,z}軸を{C_2}軸にとってもおそらく同じように係数は有理数の平方根になり, 分母の因数は2を多く含むと予想される. {z}軸を{C_3}軸, {y}軸を{C_2}軸にとるとそれは{3}になるだろう(要検証).

　そして重複度が2以上になったときの基底の効率的な決定が分からない. 一応すでに{\ell=15}どうしの合成から{\ell=30}の基底のひとつが得られているが, 280485761という大きな素数が突然現れた. 直交する基底を自然に取り出す方法があってほしい.

　今の構成法は正20面体群対称な球面上の関数が積と和について閉じることを利用している. 積としての作用が球面調和関数を基底とする空間上の線形変換になり, 欠ける次数({\ell=1,2,3,4,5,7,\cdots,29)}がそれを特徴づけている.適切な解釈が分からない.

(2/21追記)
　せっかくなので{\ell=15}のテンソル積から得られる{\ell=30}のA基底のひとつも書いておく. {\ell=30}ではA表現の重複度は2になるため, 最初の取り決めに従えば2つの空間を分けるラベルがいるがここでは無視する.

{N_{30}=5^{10}*467*280485761}
{ \begin{array}{|c|c|c|c|c|} \hline m & 0 & 5 & 10 & 15 \\ \hline c_{30,m} &13\cdot5323^2\cdot9377^2 &-2^4\cdot3\cdot11\cdot17\cdot29\cdot31\cdot 5003^2 &5\cdot7\cdot13\cdot17\cdot19\cdot23\cdot29\cdot31\cdot37\cdot1429^2 &-3^5\cdot5\cdot11\cdot13\cdot23\cdot29^3\cdot31\cdot37\cdot41\cdot43 \\ \hline \end{array} }
{ \begin{array}{|c|c|c|c|} \hline m&20 & 25 & 30\\ \hline c_{30,m} &2\cdot7\cdot29\cdot31\cdot37\cdot41\cdot43\cdot47\cdot1451^2 &2\cdot3^3\cdot11\cdot13\cdot17\cdot29\cdot31\cdot37\cdot41\cdot43\cdot47\cdot53 &7\cdot11\cdot13\cdot17\cdot19\cdot31\cdot37\cdot41\cdot43\cdot47\cdot53\cdot59\\ \hline \end{array} }

{\ell=30}球面調和関数
f:id:shironetsu:20180221013956g:plain:w500

もう一つの基底と重ね合わせて振動させたい.

f:id:shironetsu:20180220215353p:plain:w200

*1:なお, 同時に偶数次数も再度得られる. 球面調和関数であればパリティー奇と偶の積は奇でなければならないが, これはテンソル積なので問題ない. {\ell}が偶数のとき{O(3)}の忠実な表現にならないのが問題らしい, と思っている.

*2:2/21修正. 2乗和にしていた.

球面調和関数で正20面体をつくる(2) - 3j記号の非自明なゼロ

物理・数学

リベンジ

　前回, 球面調和関数の重ね合わせで{I}(正20面体群)対称性を持った関数をつくろうとしたとき取った戦略は, {SO(3)}既約表現の{I}への制限が含む恒等表現の基底への射影演算子を構成することだった. 実際に計算も行ったが, D行列の要素を位数60の群全体に渡って, さらに{(2\ell+1)\times(2\ell+1)}の要素全てを計算するという非常に迂遠な方法であった. しかもそれで得られる成分は簡潔. 正20面体に特徴的な数である{\tau=(1+\sqrt{5})/2}も消えてしまう. 何かもっと単純に計算する方法があるに違いない.
shironetsu.hatenadiary.com
　ずいぶん悩んだが, D行列成分を計算することなく係数を得るひとつの方法をようやく見つけた.　John Baezによる解説がヒントになっている.

Quantum Mechanics and the Dodecahedronjohncarlosbaez.wordpress.com

　Baezは{I}不変な{x,y,z}の多項式が,
- {P(x,y,z)=x^2+y^2+z^2}
- {Q(x,y,z)} : 正20面体の6本の対角線に平行なベクトルと{(x,y,z)}とのドット積の総乗(6次).
- {R(x,y,z)} : 正20面体の面心と中心を結ぶ独立なベクトル10本と{(x,y,z)}のドット積の総乗(10次)
- {S(x,y,z)} : 正20面体の中心と辺の中点を結ぶベクトル15本と{(x,y,z)}のドット積の総乗(15次)
　だけで書けることを示している. これと似たようなことが(あるいはひょっとすると本質的に同じことが){SO(3)}の表現の代数的な関係だけでできる.
　{\ell=1,2,3,4,5,7,8,9,11,13,14,17,19,23,29}には恒等表現が存在しなかったことが既約指標に関する考察から示されていたことを思い出しておこう.


理論

6次の場合

　まず簡単のため正20面体の{C_5}軸(5回対称軸)は{z}軸に一致すると仮定する(前回は{C_2}軸を{z}軸に取っていた).
f:id:shironetsu:20180216223534p:plain:w400
(非常にいい加減な絵だが)
するとこの正20面体と同じ対称性を持つベクトルは{m\equiv 0\ ({\rm mod}5)}に限られるため, {\ell=6}で正20面体群対称性を持つベクトルは次の形に書ける.

{ |\psi\rangle=a|65\rangle+b|60\rangle+c|6-5\rangle}

さらに{C_2}軸を{y}軸に取る. {y}軸回りの
1/2回転の表現行列は,

{ \mathcal{D}^{(\ell)}_{km}\left(\cos\frac{\pi}{2}+\sin\frac{\pi}{2}\ {\bf j}\right)=(-1)^{\ell+k}\delta_{k,-m} }

であるから, 1/2回転で

{ a|65\rangle+b|60\rangle+c|6-5\rangle \rightarrow -c|65\rangle+b|60\rangle-a|6-5\rangle }

と変換する. これで不変であるためには{a=-c}が必要. 正20面体の姿勢には{x}軸に関する反転の自由度が残るが, 今のところこれだけの条件を課す.

　さて, テンソル積を

{ |\ell_1m_1\rangle\otimes|\ell_2m_2\rangle\rightarrow |\ell_1\ell_2m_1m_2\rangle }

で表記すると, 自分自身とのテンソル積

{ |\psi\rangle |\psi\rangle=a^2|6655\rangle +b^2|6600\rangle +c^2|66\!-\!5\!-\!5\rangle\\ +ab(|6650\rangle+|6605\rangle) +bc(|660\!-\!5\rangle+|66\!-\!50\rangle) +ca(|66\!-\!55\rangle+|665\!-\!5\rangle) }

もまた{I}対称性を持つ. ここで合成系の{m=0}成分に注目する. 一般には合成系は{0\leq \ell\leq 12}成分を持つ(ただし今は明らかに対称テンソルなので偶数だけ)が, 対称性からくる制限によって{\ell=2,4,8}は許されない. すなわち,

{ \langle 80|\left(b^2|6600\rangle+ca(|66\!-\!55\rangle+|665\!-\!5\rangle)\right) =\langle 40|\left(b^2|6600\rangle+ca(|66\!-\!55\rangle+|665\!-\!5\rangle)\right)\\ =\langle 20|\left(b^2|6600\rangle+ca(|66\!-\!55\rangle+|665\!-\!5\rangle)\right)\\ =0 }

驚くべきことにこれらは次のひとつの式に同値になる:

{ 7b^2+11ca=0 }

3つの一見独立な式のこの同値性は, Clebsch-Gordan係数, あるいは3j記号の単純な性質から自明に従う結果ではない. むしろ{SO(3)}が{I}を部分群に持つことによって生じる性質と考えるべきであるように思われる.

　また, 合成系の{\ell=6}成分に注目する.

{ \langle65|ab(|6650\rangle+|6605\rangle) =-\frac{5\sqrt{11}\ ab}{\sqrt{17\cdot19}}\\ \langle 60|\left(b^2|6600\rangle+ca(|66\!-\!55\rangle+|665\!-\!5\rangle)\right) =-\frac{20\,b^2}{\sqrt{11\cdot 17\cdot 19}}+\frac{5\sqrt{11}\ ca}{\sqrt{17\cdot19}}\\ \langle6\!-\!5|bc(|660\!-\!5\rangle+|66\!-\!50\rangle) =-\frac{5\sqrt{11}\ bc}{\sqrt{17\cdot 19}} }

これらの和が元の{|\psi\rangle}の定数倍でなくてはならないが, 実はその条件

{ (-11ab):(-4b^2+11ca):(-11bc)=a:b:c }
も上の式に同値になる. さらに, 合成系の{|8,5\rangle}成分に着目する. この成分が現れるとすれば{ab}のかかる項のみで一見消えないように思える. しかし実は

{ \langle85|6650\rangle=\langle85|6605\rangle=(-1)^{6-6+5}\sqrt{2\cdot 8+1} \begin{pmatrix} 6&6&8\\5&0&-5 \end{pmatrix}=0 }

なのである({|8\!-\!5\rangle}についても同様). これもまた3j記号の性質からは直ちには言えない(と思う). 結局,

{ a=-c,\ \ \ 7b^2+11ca=0 }

に加えて規格化条件{|a|^2+|b|^2+|c|^2=1}を課し, さらに位相(phase)の不定性を消すために{a}は正実数とすると,

{ a=-c=\frac{\sqrt{7}}{5},\ \ \ b=\pm\frac{\sqrt{11}}{5} }

が得られる. {b}の符号の不定性は正20面体の姿勢の(座標の取り方の)不定性から来ているので,座標を決めれば

{ \frac{\sqrt{7}}{5}(|65\rangle-|6\!-\!5\rangle)+\frac{\sqrt{11}}{5}|60\rangle }

が(指標に関する考察から存在性は言えていてかつ唯一なので){\ell=6}表現における恒等表現の基底ということになる.

f:id:shironetsu:20180216224030g:plain:w500

　Clebsch-Gordan係数を求めるにあたって数表ないしコンピューターの力さえ借りてしまえば(ちょっとの根気さえあれば手でも求められるが)あまりにもあっけない計算だった.


10次, 12次の基底を取り出す

　さて, 上のテンソル積で{\ell=10,12}成分は消えずに残されていた({\ell=0}は無視).それぞれ以下のような成分を含んでいる.

{\ell=10}
{ -\frac{\sqrt{11}\,a^2}{\sqrt{23}}|10,10\rangle +\frac{\sqrt{3}\,\sqrt{7}\,\sqrt{19}\,ab}{\sqrt{17\cdot 23}}|10,5\rangle +\frac{49\,ca-126\,b^2}{\sqrt{13\cdot 17\cdot 19\cdot 23}} |10,0\rangle +\frac{\sqrt{3}\,\sqrt{7}\,\sqrt{19}\,bc}{\sqrt{17\cdot 23}}|10,\!-\!5\rangle -\frac{\sqrt{11}\,c^2}{\sqrt{23}}|10,\!-\!10\rangle }

{\ell=12}
{ \frac{2\sqrt{3}\, a^2}{\sqrt{23}}|12,10\rangle +\frac{{{2}^{3/2} }\,\sqrt{7}\,ab}{\sqrt{19}\,\sqrt{23}}|12,5\rangle +\frac{12\,ca+66\cdot 7\, b^2}{\sqrt{7}\,\sqrt{13}\,\sqrt{17}\,\sqrt{19}\,\sqrt{23}}|12,0\rangle +\frac{{{2}^{3/2}}\,\sqrt{7}\, bc}{\sqrt{19}\,\sqrt{23}}|12,\!-\!5\rangle +\frac{2\sqrt{3}\,c^2}{\sqrt{23}}|12,\!-\!10\rangle }

規格化すると,

{\ell=10}
{ \frac{1}{5^2\sqrt{3}}\left( \sqrt{11\cdot 17}(|10,10\rangle+|10,\!-\!10\rangle) +\sqrt{3\cdot 11\cdot 19}(-|10,5\rangle +|10,\!-\!5\rangle) +\sqrt{13\cdot 19} |10,0\rangle \right) }

f:id:shironetsu:20180216224107g:plain:w500

{\ell=12}
{ \frac{1}{5^{5/2}}\left(\sqrt{3\cdot13\cdot19}\,(|12,10\rangle+|12,\!-\!10\rangle) +\sqrt{2\cdot11\cdot13}\,(|12,5\rangle-|12,\!-\!5\rangle) +3\sqrt{7\cdot17}\,|12,0\rangle\right) }

f:id:shironetsu:20180216224134g:plain:w500

が得られる. これらがまた{\ell=10,12}表現における恒等表現の基底になる.


15次の場合

　偶数次であれば{\ell=6}のテンソル積を取ることで次々に求めていけそうだが, {\ell=15}表現はこの方法では現れない. 再び自分自身とのテンソル積を取る方法を採る.

　まず, {z}軸回りの5回対称性, {y}軸回りの2回対称性から,

{ |\phi\rangle=s(|15,15\rangle+|15,\!-\!15\rangle)+t(|15,10\rangle-|15,\!-\!10\rangle)+u(|15,5\rangle+|15,\!-\!5\rangle) }

の形に書ける. {|\ell=15, m=0\rangle$}成分は無い. 合成系の{|\ell=2,4,8,14,m=0\rangle}成分に注目すると, 上と同じ理由で

{ \langle 2,0|(|\phi\rangle|\phi\rangle)=\langle 4,0|(|\phi\rangle|\phi\rangle)=\langle 8,0|(|\phi\rangle|\phi\rangle)=\langle 14,0|(|\phi\rangle|\phi\rangle)=0 }

でなくてはならない. これは次の式に同値になる.

{ s^2:t^2:u^2=(7\cdot 11\cdot 13):(2\cdot3\cdot11\cdot29):(5\cdot23\cdot29) }

また, 合成系の{|\ell=8, 14,m=5\rangle}成分がゼロになることから,

{ (\sqrt{5\cdot23\cdot 29}\, s+\sqrt{7\cdot11\cdot13}\,u)=0 }

となる. これらが対称性から{s,t,u}に課される条件のすべてで, 規格化と位相の不定性を除く処理として{s}は正実数になるべく条件を加えると,

{ s=\frac{\sqrt{7\cdot11\cdot13}}{2\sqrt{5^5}},\ \ \ t=\pm \frac{\sqrt{2\cdot3\cdot11\cdot29}}{2\sqrt{5^5}},\ \ \ u=-\frac{\sqrt{5\cdot23\cdot29}}{2\sqrt{5^5}} }

が得られる. 上と同じように{t}の正負の不定性は{x}軸の取り方に依存しているが, 今度は上で採用した符号の取り方と両立させる必要がある. そこで合成系の{|\ell=6,m=5\rangle}と{|\ell=6,m=0\rangle}の係数の比をとると(やや込み入った計算ののち), {+}を取るべきだと分かる.まとめると,

{ \frac{1}{2\cdot5^{5/2}}\left(\sqrt{7\cdot 11\cdot 13}\,(|15,15\rangle+|15,\!-\!15\rangle) +\sqrt{2\cdot3\cdot11\cdot29}\,(|15,10\rangle-|15,\!-\!10\rangle) -\sqrt{5\cdot 23\cdot 29}\,(|15,5\rangle+|15,\!-\!5\rangle)\right) }

f:id:shironetsu:20180216224959g:plain:w500

が{\ell=15}表現の{I}の恒等表現の基底として得られる. ただし{|\ell,m\rangle\rightarrow Y^\ell_m}によって球面調和関数に置き換えるとき 純虚になるので実関数にするには{i}倍する必要がある.

……と, {\ell=6}とは独立に求めたが, この導出過程を見ると{\ell=15}の場合を考察するだけで{\ell<30}のすべての偶数の恒等表現の基底が求められるはずだと期待できる(実際にやったわけではないが)


まとめ

　射影演算子を介すことなく{I}対称な基底を取り出すという一応の目標は達成したが, 疑問も多く残る.
　依然として係数の簡潔さに比べると計算がやや冗長に感じられる. たとえば規格化された係数の分母に5の冪が現れる理由が不明瞭.
　恒等表現のテンソル積がまた恒等表現の線形結合で書ける, という条件は変数の数に対して一見過剰に見える. CG係数, 3j記号の非自明な関係式が多く生じている.
　タイトルにも付けた通り,3j記号の非自明なゼロが現れるのがかなり面白い結果だと思う. このテーマ, 3j記号, 6j記号の非自明なゼロについては不定方程式の観点から書かれた以下のような論文があった.
Brudno, Simcha. "Nontrivial zeros of the Wigner (3‐j) and Racah (6‐j) coefficients. I. Linear solutions." Journal of mathematical physics 26.3 (1985): 434-435.
http://aip.scitation.org/doi/abs/10.1063/1.526628
Brudno, Simcha. "Nontrivial zeros of the Wigner (3 j) and Racah (6 j) coefficients. II. Some nonlinear solutions." Journal of mathematical physics 28.1 (1987): 124-127.
http://aip.scitation.org/doi/abs/10.1063/1.527792
　上にも書いたが{SO(3)}が{I}を部分群に持つ事実から3j記号の色々な性質が導かれる? 今回は{C_5}軸をz軸に取ることで計算が簡単になったが, 座標に関する縛りを最小限にして進めれば関係式が色々得られるはず. 今後の課題.


f:id:shironetsu:20180216224212p:plain:w500

　

球面調和関数のレシピ - 角運動量の合成から

物理・数学

　球面上では、自分の方程式の基本解が球面調和関数になることにヤルダは気付いた。以前、地震学の講義でいちどだけお目にかかったことのある種類の波形だ。球面全体で成り立つどんな複雑な解でも、それぞれの調和振動にその寄与をあらわす適切な係数をかけて足しあわせることで表現できる。
（グレッグ・イーガン『クロックワーク・ロケット』）

　物理学では水素原子のSchrödinger方程式を解くとき, 角度方向と動径方向の変数分離をして球面上の微分作用素が{\mathfrak{so}(3)\cong\mathfrak{su}(2)}代数に従うことを利用することで球面調和関数に出会うようになっている(このあたりの歴史を自分は知らない). 物理っぽい(2次元)球面調和関数の導出法として, 他にWignerのD行列の次元を落とす方法もある. ここではスピンの合成を利用して導いてみる.

{\ell}個のスピン1系の合成によってスピン{\ell}系を得る方法は1通りしかない.

スピン1系はこのように表記する.

{|11\rangle=|+\rangle,\ \ \ |10\rangle=|+\rangle,\ \ \ |1\!-\!1\rangle=|-\rangle}

まずスピン1系を{\ell}個繋げて{m=\ell}状態を用意する.

{|\ell\ell\rangle = |+\rangle|+\rangle\cdots|+\rangle}

下降演算子を作用させて適当に規格化定数をかければ全てのスピン{\ell}状態が得られる

{|\ell m\rangle=\sqrt{\frac{(\ell+m)!}{(2\ell)!(\ell-m)!}}\ J_{-}^{\ell-m}|\ell \ell\rangle}

スピン1の状態たちは同じ空間に住んでいるものとして順序を考慮しなければ

{ J_{-}^{\ell-m}|\ell \ell\rangle=\sum_{p+q+r=\ell,\ p-r=m}A(p,q,r)|+\rangle^p(\sqrt{2}|0\rangle^q(2|-\rangle)^r }

と書ける. 0と-にかかっている{\sqrt{2}, 2}はスピン1系への下降演算子の作用で出てくるお釣り, {A}はスピン1系へ下降演算子を作用させることで{p,q,r}に辿り着く道の総数.

{A}はこのように考える. 1から{\ell}までの{|+\rangle}状態をここでは区別して, まず下降演算子を1回だけ作用させる{q}個を選ぶ. 残った中から2回作用させる{r}個を選ぶ. その{r}個については重複を許して作用させる順番を決める. 最後にその{r}個の順序をキャンセルするために{2^r}で割る. つまり,

{ A(p,q,r)={}_\ell{\rm C}_q\cdot{}_{\ell-q}{\rm C}_r\cdot \frac{(q+2r)!}{2^r}=\frac{\ell\,!(q+2r)!}{p\,!q\,!r\,!\,2^r} }

よって,

{ J_{-}^{\ell-m}|\ell \ell\rangle=\sum_{q} \frac{\ell\,!(\ell-m)!\sqrt{2^q}}{\left(\frac{\ell+m-q}{2}\right)\,!\,q\,!\left(\frac{\ell-m-q}{2}\right)\,!}\ |+\rangle^{\frac{\ell+m-q}{2}}|0\rangle^q|-\rangle^{\frac{\ell-m-q}{2}} }

変数{q}の範囲は冪が非負整数となるようなすべての整数. 規格化定数をかけて,

{|\ell m\rangle=\sqrt{\frac{\ell\,!(\ell+m)!(\ell-m)!}{2^\ell\,(2\ell-1)!!}}\sum_{q}\frac{\sqrt{2^q}}{\left(\frac{\ell+m-q}{2}\right)\,!\,q\,!\left(\frac{\ell-m-q}{2}\right)\,!}\ |+\rangle^{\frac{\ell+m-q}{2}}|0\rangle^q|-\rangle^{\frac{\ell-m-q}{2}} }

となる. さて, スピン1系は

{|+\rangle=\frac{-|x\rangle-i|y\rangle}{\sqrt{2}}\ ,\ \ |0\rangle=|z\rangle\ ,\ \ |-\rangle=\frac{|x\rangle-i|y\rangle}{\sqrt{2}}}

であった. 球面上の関数として

{\frac{-x-iy}{\sqrt{2}}=\frac{-\sin\theta\,e^{i\varphi}}{\sqrt{2}}\ ,\ \ z=\cos\theta\ ,\ \ \frac{x-iy}{\sqrt{2}}=\frac{\sin\theta\,e^{-i\varphi}}{\sqrt{2}}}

も同じ代数に従い, 3つに共通の定数倍の違いを除いて{\ell=1}の球面調和関数に等しい. 一般の{\ell}について, その規格化定数は球面上の積分を内積として定義されるべきであり,{|\ell \ell\rangle}に対して

{\int_{S^2}dS\left(\frac{x^2+y^2}{2}\right)^\ell=\int_{\theta=0}^\pi\int_{\varphi=0}^{2\pi}\sin\theta d\theta d\varphi \left(\frac{\sin^2\theta}{2}\right)^\ell=\frac{4\pi\,\ell\,!}{(2\ell+1)!!} }

の逆数の平方根. 結局,

{ Y^\ell_m=\frac{\sqrt{(2\ell+1)(\ell+m)!(\ell-m)!}}{\sqrt{4\pi}} \sum_{q} \frac{(-x-iy)^{\frac{\ell+m-q}{2}} z^q (x-iy)^{\frac{\ell-m-q}{2}}} {2^{\ell-q}\left(\frac{\ell+m-q}{2}\right)\,!\,q\,!\left(\frac{\ell-m-q}{2}\right)\,!}\\=\frac{\sqrt{(2\ell+1)(\ell+m)!(\ell-m)!}}{\sqrt{4\pi}} \sum_{k={\rm max}\{0,m\}}^{\lfloor(\ell+m)/2\rfloor} \frac{(-1)^k(x+iy)^kz^{\ell+m-2k}(x-iy)^{k-m}}{2^{2k-m}k!(\ell+m-2k)!(k-m)!}\\=\frac{\sqrt{(2\ell+1)(\ell+m)!(\ell-m)!}}{\sqrt{4\pi}} \sum_{k={\rm max}\{0,m\}}^{\lfloor(\ell+m)/2\rfloor} \frac{(-1)^k\sin^{2k-m}\theta\cos^{\ell+m-2k}\theta\ e^{im\varphi}}{2^{2k-m}k!(\ell+m-2k)!(k-m)!} }

という表式を得る(ほんとうは{4\pi}の因子は面積要素のほうに押し付けたい). x,y,z座標での表示が先に出てきて便利. これを使って正20面体対称性を持った多項式の形を見ていきたい(続).

(追記)
　確認のため利用したMaximaで使われている定義とはmが奇数の時だけ-1倍違った. この-1倍というのは下降演算子の作用に由来している. これをCondon - Shortley phaseというらしい.
Condon-Shortley Phase -- from Wolfram MathWorld
　2人は角運動量固有状態間の位相についての取り決めを定めた有名な本の著者. Clebsch - Gordan係数表はだいたいCondon - Shortley conventionに従っている. それを思うと球面調和関数の定義がいまいちよく統一されていないのはよく分からない.

球面調和関数で正20面体をつくる

物理・数学

正20面体とむきあう

　Greg Egan先生がTwitterアカウント等で昨年末から公開している動画.


plus.google.com

　球面調和関数を組み合わせることで多面体の対称性を持たせている.

　John Baez先生*1もこれに関して色々書かれている(例外型Lie群E8との関わりもあるらしく深い).
Quantum Mechanics and the Dodecahedron | Azimuth

　折しも私個人大学の課題で似たようなことを考える必要に迫られていてホットなテーマに感じられたのでこのおもちゃで遊んでみる.

理論

SU(2), SO(3)ミニマム

　2次ユニタリ群SU(2)の任意の元gは次の形を持つ.
{ g=\begin{pmatrix} a&-\overline{b}\\ b&\overline{a} \end{pmatrix} \ \ \ |a|^2+|b|^2=1,\ a,b\in\mathbb{C} }
SU(2)の既約な(2j+1)次元ユニタリ表現はWignerのD行列で得られる. その成分は,

{ \mathcal{D}^{(j)}_{km}(g)=\sum_{\nu=\max\{0,\,k-m\}}^{\min\{j+k,\,j-m\}}\frac{(-1)^\nu}{\nu!} \frac{\sqrt{(j+m)!(j-m)!(j+k)!(j-k)!}}{(j+k-\nu)!(m-k+\nu)!(j-m-\nu)!} a^{j+k-\nu}b^{m-k+\nu}\overline{b}^\nu\overline{a}^{j-m-\nu} }

と表せる. ただしjは0, 1/2, 1, 3/2,…の整数または半整数. 行列番号のk, mはjから始まって-jまで下る形で書くことを想定する. たとえばj=1のとき,

{ \mathcal{D}^{(1)}(g)= \begin{pmatrix} \mathcal{D}^{(1)}_{11} & \mathcal{D}^{(1)}_{10} & \mathcal{D}^{(1)}_{1-1} \\ \mathcal{D}^{(1)}_{01} & \mathcal{D}^{(1)}_{00} & \mathcal{D}^{(1)}_{0-1} \\ \mathcal{D}^{(1)}_{-11} & \mathcal{D}^{(1)}_{-10} & \mathcal{D}^{(1)}_{-1-1} \end{pmatrix}= \begin{pmatrix} a^2 & - \sqrt{2}a\overline{b} & \overline{b}^2\\ \sqrt{2}ab & |a|^2-|b|^2 & - \sqrt{2}\overline{a}\overline{b}\\ b^2 & \sqrt{2}\overline{a}b & \overline{a}^2 \end{pmatrix} }

特にこの場合, ユニタリ行列Uによる相似変換でSO(3)の元と1対1に対応する.

{ U=\begin{pmatrix}-1/\sqrt{2}&0&1/\sqrt{2}\\-i/\sqrt{2}&0&-i/\sqrt{2}\\0&1&0\end{pmatrix}\\ U\mathcal{D}^{(1)}(g)U^\dagger=\begin{pmatrix} {\rm Re}(a^2-b^2) &{\rm Im}(a^2-b^2) &2{\rm Re}(a\overline{b}) \\-{\rm Im}(a^2+b^2)&{\rm Re}(a^2+b^2) &-2{\rm Im}(a\overline{b}) \\-2{\rm Re}(ab) &-2{\rm Im}(ab)&|a|^2-|b|^2\end{pmatrix}\in SO(3) }

つまりSO(3)の表現. 一般に, jが整数の時はSO(3)の表現になる. というのも, SU(2)の元をその(-1)倍と同一視する(正規部分群{Z_2=\{1,-1\}}による剰余群)とSO(3)と同型であり,

{ SU(2)/Z_2\cong SO(3) }

上の式を見れば明らかなように,

{ \mathcal{D}^{(\ell)}(-g)=\mathcal{D}^{(\ell)}(g)\ \ \ \ell:{\rm integer} }

が成り立っているため(整数次のD行列の次数は{\ell}で表すようにする.).

　逆に半整数次の場合はSO(3)の表現ではない. が, Z2による共役類とは一対一に対応する. あまり適切な用語ではないようだが, これを2価表現と呼び本記事でも使うことにする.

　上の同型は次のように構成できる. まず四元数をPauli行列の-i倍と同一視する.

{ {\bf i}=\begin{pmatrix}0&-i\\-i&0\end{pmatrix},\ {\bf j}=\begin{pmatrix}0&-1\\1&0\end{pmatrix},\ {\bf k}=\begin{pmatrix}-i&0\\0&i\end{pmatrix},\ }

するとSU(2)は次のように表せる*2.

{ SU(2)=\{\alpha+\beta{\bf i}+\gamma{\bf j}+\delta{\bf k}\mid\alpha^2\!+\!\beta^2\!+\!\gamma^2\!+\!\delta^2=1,\ \alpha,\beta,\gamma,\delta\in\mathbb{R}\} }

{\mathbb{R}^3}線形空間Vを

{ V={\rm Span}_{\mathbb R}\langle {\bf i},\ {\bf j},\ {\bf k}\rangle }

で定義すると, 次の{\varphi}はSU(2)からV上のSO(3)変換への写像になる.

{ \varphi : SU(2)\rightarrow SO(3)\\ \varphi(g)x=gxg^\dagger\ \ \ x\in V }

特に, 軸(nx,ny,nz)回りの角θの回転は

{ g=\pm\left(\cos\frac{\theta}{2}+\sin\frac{\theta}{2}(n_x{\bf i}+n_y{\bf j}+n_z{\bf k})\right)\ \ \ (n_x^2+n_y^2+n_z^2=1) }

で表せる. このとき固有値{e^{\pm i\theta/2}}. j次の既約表現のトレースは,

{ {\rm Tr}(\mathcal{D}^{(j)}(g))=\sum_{k=-j}^j\mathcal{D}^{(j)}_{kk} \begin{pmatrix}e^{i\theta/2}&0\\0& e^{-i\theta/2}\end{pmatrix}= \sum_{k=-j}^j(e^{i\theta/2})^{j+k}(e^{-i\theta/2})^{j-k}= \sum_{k=-j}^je^{ik\theta} }

これを利用してまず解くのは次の問題. 整数次のD行列による正20面体群の表現は既約表現の直和としてどのように分解されるか?


正20面体を回す

　よく知られているように, 正12面体, 正20面体の(空間の向きを変えない)回転対称性の群 I (Icosahedral group; 正12面体群dodecahedral groupと同型だが一般には正20面体のほうで代表するらしい)は5次の交代群A5と同型になっている. これを理解するにはまず次のように各面に1から5までの数を振る. 括弧は背面の数. 各頂点のまわりに1から5まですべて集まるようになっている.
f:id:shironetsu:20180210224233p:plain:w300
　この展開図を次の2通りの方法で描く.
f:id:shironetsu:20180210224136p:plain:w300
　頂点と中心を結ぶ軸まわりに回転させると(12345)の置換.
f:id:shironetsu:20180210224148p:plain:w300
　面心と中心を結ぶ軸回りに回転させると(254)の置換.

　I, またはA5全体はこのふたつから生成される.

τを次で定義する.

{ \tau=\frac{1+\sqrt{5}}{2}=2\cos\frac{\pi}{5}\\ \tau^2-\tau-1=0 }

これを使うと辺長1の正20面体の12個の頂点は,

{ (\pm\tau, \pm 1, 0),\ (0, \pm\tau, \pm 1),\ (\pm 1, 0, \pm\tau) }

で表せる.
f:id:shironetsu:20180210224315p:plain:w300
組み合わされている3枚の長方形の長辺は短辺1に対してτ.
これらはまた正12面体の面(正5角形)の中心でもあるから, ひとつ選んで原点と結んだ直線を軸に1/5回転させると対称変換になる. いま(τ,1,0)を選ぶと, 対応する四元数は

{ r=\cos\frac{\pi}{5}+\sin\frac{\pi}{5}\cdot\frac{\tau {\bf i}+{\bf j}}{\sqrt{\tau^2+1}}= \frac{1}{2}\left(\tau + {\bf i} + \frac{1}{\tau}{\bf j}\right)= \frac{1}{2}\begin{pmatrix}\tau& -1/\tau-i \\ 1/\tau-i & \tau\end{pmatrix} }

2/5回転は2回繰り返して

{ r^2 = \frac{1}{2}\begin{pmatrix}1/\tau & -1-\tau i \\ 1-\tau i & 1/\tau\end{pmatrix} }

一方, 正20面体の面(正3角形)の中心と原点を結んだ直線を軸にした1/3回転も対称変換. (1,1,1)を通る直線を選ぶと,

{ s = \cos\frac{\pi}{3} + \sin\frac{\pi}{3}\frac{{\bf i}+{\bf j}+{\bf k}}{\sqrt{3}}=\frac{1}{2}\left(1+{\bf i}+{\bf j}+{\bf k}\right)=\frac{1}{2}\begin{pmatrix}1-i & -1-i\\ 1-i & 1+i \end{pmatrix} }

さらに,

{ rs=\frac{1}{2}\begin{pmatrix}-i&-1/\tau-\tau i\\ 1/\tau-\tau i&i\end{pmatrix},\ \ \ (rs)^2 = -1 }

と, rsは1/2回転に対応.

まとめると, 次のように対応している.

f:id:shironetsu:20180210224817p:plain:w500

なお2価表現は代表元ひとつをとっている(以下でも特に断りなくそうする). 2価表現はSU(2)の有限部分群として位数は2倍の120となっているが, これを二重正20面体群 2I と呼んでおく*3. 話が前後するが, 次節で説明するように, 上の表のそれぞれが共役類の代表元になっている.

　なお, A5は次の表示(presentation)を持つ

{ A_5\cong I\cong\langle x,y\mid x^5=y^3=(xy)^2=1\rangle }

正20面体群の共役類

　A5の共役類を調べる. 対称群の共役類は置換の型で決まるが, 交代群ではそうではない. A5は対称群S5の部分群として,

[5]型…(12345)のS5共役元…24個
[3,1,1]型…(123)のS5共役元…20個
[2,2,1]型…(12)(34)のS5共役元…15個
[1,1,1,1,1]型…e(恒等置換)…1個

を含むが, このうち[5]型はA5上では半分の共役類に分かれる. すなわちA5型の共役元のリストは次の通り.

[5]型…(12345)のA5共役元…12個
[5]型…(13524)のA5共役元…12個
[3,1,1]型…(123)のA5共役元…20個
[2,2,1]型…(12)(34)のA5共役元…15個
[1,1,1,1,1]型…e(恒等置換)…1個

　これは正20面体の回転としてとらえると分かりやすい.
　(12345)はあるひとつの頂点-中心軸回りの左回り1/5回転=右回り4/5回転に対応する. 対蹠点では右回り1/5回転=左回り4/5回転になっている. したがってこのような回転は頂点の数だけあり, 12個. (13524)型は(12345)の2乗だから, 2/5回転で同様に12個.
　(123)はあるひとつの面心-中心軸回りの左回り1/3回転=右回り2/3回転. 対蹠点では右回り1/3回転=左回り2/3回転. 面の数だけあり, 20個.
　(12)(34)は辺の中点-中心軸回りの1/2回転であり, 対蹠点でのそれと一致. したがって裏表の辺のペアの数だけあり, 30/2=15個. 恒等変換は当然1個.

　化学などでの用法に従って, 各共役類について, 1/5回転を{C_5}, 2/5回転を{C_5^2}, 1/3回転を{C_3}, 1/2回転を{C_2}, 恒等変換を{E}と呼ぶことにする.


正20面体群の既約表現

　共役類は5つ. 従って既約表現も5つ. 自明な表現を除いた4つの既約表現の次元の二乗和は位数-1で59. そのような自然数の組はひとつしかない(ちなみに0を含んでよければ他に(0,1,3,7), (0,3,5,5)がある.).

{ 3^2+3^2+4^2+5^2=59 }

それぞれの次元に対応した既約表現を作ろう.

1次元表現

　Aと呼ばれる表現*4. これは自明な表現ですべて1.

3次元表現その1

{T_1}表現と呼ぶ. SO(3)部分群としての正20面体群の定義表現を含む. これはたとえばD行列によって

{ T_1(g)=U\mathcal{D}^{(1)}(g)U^\dagger\in SO(3) }

ととればよい

{ T_1(r)= \frac{1}{2}\begin{pmatrix}\tau & \tau^{-1} & 1\\ \tau^{-1} & 1 & -\tau\\-1 & \tau & \tau^{-1} \end{pmatrix},\ \ \ T_1(r^2)=\frac{1}{2}\begin{pmatrix}1 & \tau & \tau^{-1}\\ \tau & -\tau^{-1} & -1\\-\tau^{-1} & 1 & -\tau\end{pmatrix}\\ T_1(s)=\begin{pmatrix}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{pmatrix},\ \ \ T_1(rs)= \frac{1}{2}\begin{pmatrix}\tau^{-1}& 1 & \tau\\ 1 & -\tau & \tau^{-1}\\ \tau & \tau^{-1} & -1\end{pmatrix} }

指標は{C_5:\tau, C_5^2:-1/\tau, C_3: 0, C_2:-1, E:3}.

3次元表現その2

{T_2}表現と呼ぶ. これを作るにはS5の内部自己同型でA5の外部自己同型となる写像を使う.
{C_5}と{C_5^2}は対称群の元としては共役なのだった. たとえば,

{ (1325)(12345)(1325)^{-1}=(12345)^2\\ (1325)(254)(1325)^{-1}=(145)=(254)^2(12345)^2(254)^2(12345)^3(254) }

から, 生成元ふたつに対して同型写像を

{ \varphi(r)=r^2,\ \ \ \varphi(s)=s^2r^2s^2r^3s }

とすればよい. よって,

{ T_2(r)=T_1(r^2),\ \ \ T_2(r^2)=T_1(r)\\ T_2(s)=T_1(s^2r^2s^2r^3s)= \frac{1}{2}\begin{pmatrix}-1 & \tau & \tau^{-1}\\-\tau & -\tau^{-1} & -1\\-\tau^{-1} & -1 & \tau \end{pmatrix},\ \ \ T_2(rs)=T_1(rs^2r^2s^2r^3s)=\begin{pmatrix}-1&0&0\\ 0&1&0\\ 0&0&-1 \end{pmatrix} }

指標は{C_5:-1/\tau,\ C_5^2:\tau,\ C_3:0,\ C_2:-1,\ E:3}.

4次元表現

　{G}と呼ばれる表現. まず対称群の元として5×5の置換行列を作る.

{ P_5(\sigma)_{ij}=\delta_{i\sigma(j)}\ \ \ \sigma\in S_5 }
{ P_5(r)=\begin{pmatrix} 0&0&0&0&1\\ 1&0&0&0&0\\ 0&1&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&0 \end{pmatrix},\ \ \ P_5(s)=\begin{pmatrix} 1&0&0&0&0\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1\\ 0&1&0&0&0 \end{pmatrix} }

あきらかに{(1,1,1,1,1)^T}の張る1次元空間がこれらで不変だから可約.

{ \varOmega_{mn}=\frac{\zeta^{mn}}{\sqrt{5}}\ \ \ \left(\zeta:=\exp\left(\frac{2\pi i}{5}\right)\right) }

なる5次ユニタリ行列(離散Fourier変換に使うもの)によって,

{ \varOmega P(r)\varOmega^\dagger =\begin{pmatrix} G(r)&0\\ 0&1 \end{pmatrix},\ \ \ \varOmega P(s)\varOmega^\dagger= \begin{pmatrix} G(s)&0\\ 0&1 \end{pmatrix} }

とブロック対角にできる. ここに4次正方行列Gは以下の通り.

{ G(r)=\begin{pmatrix} \zeta&0&0&0\\ 0&\zeta^2&0&0\\ 0&0&\zeta^3&0\\ 0&0&0&\zeta^4 \end{pmatrix},\ \ \ G(s)= \frac{1}{\sqrt{5}} \begin{pmatrix} \zeta^4&\zeta^4/\tau&\tau \zeta^4&-\zeta^4\\\zeta^3/\tau&-\zeta^3&\zeta^3&\tau \zeta^3\\ \tau\zeta^2&\zeta^2&-\zeta^2&\zeta^2/\tau\\-\zeta&\tau \zeta&\zeta/\tau &\zeta \end{pmatrix}\\ G(r^2)=\begin{pmatrix} \zeta^2&0&0&0\\ 0&\zeta^4&0&0\\ 0&0&\zeta&0\\ 0&0&0&\zeta^3 \end{pmatrix},\ \ \ G(rs)=\frac{1}{\sqrt{5}} \begin{pmatrix} 1&1/\tau&\tau&-1\\1/\tau&-1&1&\tau\\ \tau&1&-1&1/\tau\\-1&\tau&1/\tau&1 \end{pmatrix} }

指標は

{C_5 : -1,\ C_5^2 : -1,\ C_3 : 1,\ C_2 : 0,\ E:4}

5次元表現

　{H}と呼ばれる表現.
　まず6次対称群への準同型から置換行列によって6次元表現を作る(6次対称群の外部自己同型に関係している).
　正20面体の中心を通る対角線は全部で6本. 正20面体の回転はそれらの置換になるから, ラベリングすれば6次対称群の部分群との同型が得られる.
展開図を再掲. 新たに各頂点に割り当てた色は6つの対角線に対応.

f:id:shironetsu:20180210225140p:plain:w600

White(1), Yellow(2), Magenta(3), Orange(4), Green(5), Blue(6)の置換とすると,

{ r : (12345)\in A_5 \leftrightarrow (\!(23456)\!)\in S_6\\ s : (254)\in A_5 \leftrightarrow (\!(123)\!)(\!(465)\!)\in S_6 }

の対応関係が付く(混同の無いようにS6の元は二重括弧で括った). 6次の置換行列で表すと,

{ P(\!(23456)\!)= \begin{pmatrix} 1&0&0&0&0&0\\ 0&0&0&0&0&1\\ 0&1&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0 \end{pmatrix},\ \ \ P(\!(123)\!)(\!(465)\!)= \begin{pmatrix} 0&0&1&0&0&0\\ 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1\\ 0&0&0&1&0&0 \end{pmatrix} }

これもまた明らかに可約.

{ Z_{mn}=\frac{(-\omega^2)^{mn}}{\sqrt{6}}\ \ \ \left(\omega:=\exp\left(\frac{2\pi i}{3}\right),\ \ \ -\omega^2=\exp\left(\frac{\pi i}{3}\right)\right) }

なるユニタリ行列によって,

{ ZP(\!(23456)\!)Z^\dagger= \begin{pmatrix} H(r)&0\\ 0& 1\end{pmatrix},\ \ \ ZP(\!(123)\!)(\!(465)\!)Z^\dagger= \begin{pmatrix} H(s)&0\\ 0&1\end{pmatrix} }

とブロック対角化. ただし,

{ H(r)=\frac{1}{6}\begin{pmatrix}-5\omega^2&\sqrt{3}\,i\omega&-2&-\sqrt{3}\,i\omega^2&\omega\\ \sqrt{3}\,i\omega^2&3\omega&-2\sqrt{3}\, i&3\omega^2&\sqrt{3}\,i\omega\\-2\omega^2&-2\sqrt{3}\, i\omega&-2&2\sqrt{3}\, i\omega^2&-2\omega\\-\sqrt{3}\, i\omega^2&3\omega&2\sqrt{3}\, i&3\omega^2&-\sqrt{3}\,i\omega\\ \omega^2&\sqrt{3}\, i\omega&-2&-\sqrt{3}\,i\omega^2&-5\omega \end{pmatrix}\,\ \ \ H(s)=\frac{1}{6}\begin{pmatrix} 1&2\sqrt{3}\,i\omega^2&-2\omega&\sqrt{3}\,i&4\omega^2\\2\sqrt{3}\,i\omega&-3&-2\sqrt{3}\,i&0&-\sqrt{3}\,i\\-2\omega^2&2\sqrt{3}\,i\omega&-2&-2\sqrt{3}\,i\omega^2&-2\omega\\ \sqrt{3}\,i&0&-2\sqrt{3}\,i\omega&-3&-2\sqrt{3}\,i\omega^2\\4\omega&-\sqrt{3}\,i&-2\omega^2&-2\sqrt{3}\,i\omega&1 \end{pmatrix}\\ H(r^2)=\frac{1}{6}\begin{pmatrix}-1+3\omega&2\sqrt{3}\,i&2\omega^2&-\sqrt{3}\,i\omega^2&2\omega\\-2\sqrt{3}\,i\omega&-3\omega&-2\sqrt{3}\,i\omega&0&\sqrt{3}\,i\omega\\2\omega&2\sqrt{3}\,i&2&2\sqrt{3}\,i\omega&2\omega^2\\-\sqrt{3}\,i\omega^2&0&2\sqrt{3}\,i\omega^2&-3\omega^2&2\sqrt{3}\,i\omega^2\\2\omega^2&\sqrt{3}\,i\omega&2\omega&2\sqrt{3}\,i&-1+3\omega^2 \end{pmatrix},\ \ \ H(rs)=\frac{1}{2}\begin{pmatrix} 0&-\sqrt{3}\,i\omega&0&0&-\omega\\ \sqrt{3}\,i\omega^2&0&0&-\omega^2&0\\ 0&0&2&0&0\\0&-\omega&0&0&-\sqrt{3}\,i\omega\\-\omega^2&0&0&\sqrt{3}\,i\omega^2&0 \end{pmatrix} }

　指標は{C_5:0,\ C_5^2:0,\ C_3:-1,\ C_2:1,\ E:5}


　こうして完全な指標表を得る. 同値でない表現の指標どうしの直交性, 各表現で指標の2乗和が位数60に等しいと確かめられることからこの正しさが保証される.

f:id:shironetsu:20180210220601p:plain:w500


D行列表現の既約分解

　SU(2)の{\ell}次D行列表現では

{ \chi_\ell(C_5)=\sum_{k=-\ell}^\ell\zeta^k=1+2\sum_{k=1}^\ell \cos\frac{2\pi k}{5}=1+\frac{1}{\tau}-\tau-\tau+\frac{1}{\tau}+2\cdots\\ \chi_\ell(C_5^2)=\sum_{k=-\ell}^\ell\zeta^{2k}=1+2\sum_{k=1}^\ell \cos\frac{4\pi k}{5}= 1-\tau+\frac{1}{\tau}+\frac{1}{\tau}-\tau+2-\cdots\\ \chi_\ell(C_3)=\sum_{k=-\ell}^\ell\omega^k=1+2\sum_{k=1}^\ell \cos\frac{2\pi k}{3}=1-1-1+2-1-1+\cdots\\ \chi_\ell(C_2)=\sum_{k=-\ell}^\ell(-1)^k=1-2+2-2+2-\cdots\\ \chi_\ell(E)=\sum_{k=-\ell}^\ell 1^k=2\ell+1 }

であった. これと指標表を利用すると, 直和分解で各既約表現を含む回数(重複度)が求められる. 表にすると以下の通り.

{\ell} 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
A 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 2
T1 0 1 0 0 0 1 1 1 0 1 1 2 1 1 1 2 2 2 1 2 2 3 2 2 2 3 3 3 2 3 3
T2 0 0 0 1 0 1 0 1 1 1 1 1 1 2 1 2 1 2 2 2 2 2 2 3 2 3 2 3 3 3 3
G 0 0 0 1 1 0 1 1 1 2 1 1 2 2 2 2 2 2 3 3 2 3 3 3 4 3 3 4 4 4 4
H 0 0 1 0 1 1 1 1 2 1 2 2 2 2 3 2 3 3 3 3 4 3 4 4 4 4 5 4 5 5 5

(各{\ell}に対する各既約表現の重複度)

　E以外の指標はそれぞれ5,3,2の周期を持つため合わせて30の周期になる. 従って{\ell=30}以上では{(\ell-30)}との差がEからの寄与だけで, 重複度はの増分は次元の数に等しい.

　さて, いま興味があるのは実際にはA表現だけ. すべての元に対して不変, すなわち固有値1の部分空間を探しているのだった. 表を見ればわかるように自明な{\ell=0}を除けば初めてI-不変なテンソルが存在できるのは{\ell=6}. 続いて10, 12, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28と来て, 30で初めて固有空間が2次元になる. 逆に存在できない{\ell}は29以下のいくつかに限られる. それらの共通の性質が6,10,15の和で表せないこと(この事実自体は母関数generating functionを作って確かめることもできる)であってその代数的な意味付けがある, というのがBaezのウェブサイトなどで語られているが呑み込めていない.

　全ての既約表現の重複度を調べたが, Aについてだけなら実はもっと簡単な考察から調べられる.


射影演算子

　一般に, 群Gの表現空間で全ての元に対して不変なベクトルを作りたければ, 勝手なベクトルに対してすべての元を作用させたものの和を取ればいい. 射影演算子を次のように定める:

{ P_G:=\frac{1}{|G|}\sum_{g\in G}D(g) }

容易にわかるように, {P_G^2=P_G}. また, 全てのa∈Gに対して

{ D(a)P_G=\frac{1}{|G|}\sum_{g\in G}D(ag)=P_G }

であるから, 表現空間の任意の元に作用させても

{ D(a)(P_G|x\rangle)=P_G|x\rangle }

と不変, すなわち固有値1の固有ベクトルになる. 逆に全てのaに対して固有値1なら

{|x\rangle=P_G|x\rangle }

と表せる.
{P_G}の固有値1の規格直交化された固有ベクトルたちを|1k〉(kは異なる固有ベクトルを区別するラベル)とすると(対角化が可能だとして)

{ P_G=\sum_{k=1}^f|1_k\rangle\!\langle 1_k| }

で表せる. fは固有値1の固有空間の次元. この式の両辺のトレースを取ることによって,

{ \frac{1}{|G|}\sum_{g\in G}\chi(g)=f }

を得る. χは指標. 上と同じ結果が得られる.


3次元球面上の点として

　正20面体の表現の素性を知るべくいろいろ調べたが, 結局使うのはこの1次元表現基底Aへの射影演算子だけ. これをどう計算するか.

　二重正20面体群の120個の元を列挙するのは実は簡単. 上で使った正20面体の頂点の座標を使うと, x,y,zに関して反転対称, x→y→z→xの入れ替えで巡回対称であることは明らか. SU(2)の元を次のように3次元球面上の座標で表すと, それぞれ以下のようになる.

{ \alpha+\beta{\bf i}+\gamma{\bf j}+\delta{\bf k}\in SU(2)\leftrightarrow (\alpha,\beta,\gamma,\delta)\in S^3 }

  • 1/5回転{C_5}

{ \frac{1}{2}(\pm\tau,\,\pm 1,\,\pm\tau^{-1},\,0),\ \ \ \frac{1}{2}(\pm\tau,\,0,\,\pm 1,\,\pm\tau^{-1}),\ \ \ \frac{1}{2}(\pm\tau,\,\pm\tau^{-1},\,0,\,\pm 1) }

  • 2/5回転{C_5^2}

{ \frac{1}{2}(\pm\tau^{-1},\,\pm\tau,\,\pm1,\,0),\ \ \ \frac{1}{2}(\pm\tau^{-1},\,0,\,\pm\tau,\,\pm1),\ \ \ \frac{1}{2}(\pm\tau^{-1},\,\pm1,\,0,\,\pm\tau) }

  • 1/3回転{C_3}

{ \frac{1}{2}(\pm 1,\,\pm 1,\,\pm 1,\,\pm 1),\ \ \ \frac{1}{2}(\pm 1,\,0,\,\pm\tau^{-1},\,\pm\tau),\ \ \ \frac{1}{2}(\pm 1,\,\pm\tau^{-1},\,\pm\tau,\,0),\ \ \ \frac{1}{2}(\pm 1,\,\pm\tau,\,0,\,\pm\tau^{-1}),\ \ \ }

  • 1/2回転{C_2}

{ (0,\,1,\,0,\,0),\ \ \ (0,\,0,\,1,\,0),\ \ \ (0,\,0,\,0,\,1)\\ \frac{1}{2}(0,\,\pm\tau,\,\pm\tau^{-1},\,\pm1),\ \ \ \frac{1}{2}(0,\,\pm1,\,\pm\tau,\,\pm\tau^{-1}),\ \ \ \frac{1}{2}(0,\,\pm\tau^{-1},\,\pm1,\,\pm\tau),\ \ \ }

  • 恒等変換{E}

{ (\pm 1,\,0,\,0,\,0) }

内訳は
{(0,\,\pm 1,\,\pm \tau,\,\pm\tau^{-1})}を偶置換で入れ替えたもの合計96個,
{(\pm1,\pm1,\pm1,\pm1)}で16個,
{(\pm1,0,0,0)}の巡回置換8個
となっている.

これを使って数式処理ソフトによって力任せにA基底を求める. l=0は自明(球対称;SO(3)対称)なので正20面体対称性をもつ最小のl=6から.

{ \frac{\sqrt{5}\,\sqrt{21}}{32}\Big(|6,6\rangle+|6,-6\rangle\Big)-\frac{\sqrt{11}\,\sqrt{14}}{32}\Big(|6,4\rangle+|6,-4\rangle\Big)-\frac{\sqrt{7}\,\sqrt{11}\,\sqrt{3}}{32}\Big(|6,2\rangle+|6,-2\rangle\Big)+\frac{\sqrt{11}}{16}\,|6,0\rangle }

2次元球面上の関数空間の基底;球面調和関数で表すと

{ \frac{\sqrt{5}\,\sqrt{21}}{32}\Big(Y^6_6+Y^6_{-6}\Big)-\frac{\sqrt{11}\,\sqrt{14}}{32}\Big(Y^6_4+Y^6_{-4}\Big)-\frac{\sqrt{7}\,\sqrt{11}\,\sqrt{3}}{32}\Big(Y^6_2+Y^6_{-2}\Big)+\frac{\sqrt{11}}{16}\,Y^6_0 }

これを球面上に色でプロットしたものが下のアニメーション.

f:id:shironetsu:20180210225407g:plain

サッカーボール. 正しい道を辿っていたことが分かった.

10,12の場合の表式も見ておく.

{\ell=10}

{-\frac{\sqrt{3\cdot 5\cdot 11\cdot 17}}{256}\Big(|10,10\rangle+|10,-10\rangle\Big)-\frac{\sqrt{2\cdot 5\cdot 11\cdot 17\cdot 19}}{256\sqrt{3}}\Big(|10,8\rangle+|10,-8\rangle\Big)+\frac{\sqrt{11\cdot 19}}{256} \Big(|10,6\rangle+|10,-6\rangle\Big)\\-\frac{\sqrt{2\cdot 5\cdot 11\cdot 19}}{128} \Big(|10,4\rangle+|10,-4\rangle\Big)+\frac{\sqrt{2\cdot 11\cdot13\cdot 19}}{256\,} \Big(|10,2\rangle+|10,-2\rangle\Big)+\frac{5\sqrt{13\cdot 19}}{128\sqrt{3}}|10,0\rangle }

{\ell=12}

{ \frac{3\sqrt{5\cdot 13\cdot 19\cdot 23}}{2048} \Big(|12,12\rangle+|12,-12\rangle\Big) -\frac{11\sqrt{3\cdot 13\cdot 19}}{1024} \Big(|12,10\rangle+|12,-10\rangle\Big)+ \frac{\sqrt{2\cdot 3\cdot 7\cdot 11\cdot 13 \cdot 19}}{2048\sqrt{5}} \Big(|12,8\rangle+|12,-8\rangle\Big)\\+ \frac{3\cdot 5\,\sqrt{7\cdot 11\cdot 13}}{1024} \Big(|12,6\rangle+|12,-6\rangle\Big)+ \frac{17\sqrt{11\cdot 13\cdot 17}}{2048\sqrt{5}} \Big(|12,4\rangle+|12,-4\rangle\Big) -\frac{\sqrt{2\cdot 3\cdot 11\cdot 13\cdot 17}}{1024} \Big(|12,2\rangle+|12,-2\rangle\Big)\\+ \frac{3\cdot 29\sqrt{7\cdot 17}}{1024\sqrt{5}} |12,0\rangle }

　こうして見ると因数が多いとはいえ係数はかなり簡単な形をしていることが分かる. どうすればもっと簡単に求められるのだろう?

　イーガンはl=6の場合についてC5軸(5回対称軸)をz軸に取ることで3つのJz固有ベクトルの和としてこれを表していた.

{ \frac{1}{5}\Big(\sqrt{7}|6,5\rangle+\sqrt{11}|6,0\rangle-\sqrt{7}|6,-5\rangle\Big) }

いかにも手計算で求められそうな簡潔な式.

　たとえば上に列挙した二重正20面体が鏡系をなすこと*5など使えそうな対称性はいくつかあるものの現状未解決.

　鏡といえば正20面体対称かつパリティー奇のものは{\ell=15}で初めて許されるという話題もあった. これは{\ell}の偶奇がそのまま球面調和関数のパリティーに対応することからすぐ分かる.


まとめ

　正20面体群の既約表現を求め, SO(3)の部分群としてWigner D行列による表現を直和分解した. そこから自明な1次元表現Aの基底への射影演算子によって不変な成分を見つけた. その過程で数式処理ソフトを用いたが, 手計算できる程度にまで問題を落としたい.

リファレンス

  • www.math.lsa.umich.edu/~kesmith/Icosahedron.pdf

大学のレポート問題? このヒントに従って既約表現を求めてみた. ただ交代群はこういった発見的な方法より, Young図形を使ってもっと系統的に調べられると思う.

  • Cohan, N. (1958). The spherical harmonics with the symmetry of the icosahedral group. Mathematical Proceedings of the Cambridge Philosophical Society, 54(1), 28-38. doi:10.1017/S0305004100033156

The spherical harmonics with the symmetry of the icosahedral group | Mathematical Proceedings of the Cambridge Philosophical Society | Cambridge Core
ドンピシャなタイトル. 60年以上前の論文だがコンピューターで数値計算している.

  • Peter Atkins, Julio de Paula『アトキンス物理化学(上)』(千原秀昭, 中村亘男 訳), 東京化学同人(2009)

　ちなみにランダウ量子力学には分子対称性としては存在しないとのことで指標表が載っていなかった…はず(手元にないため要確認). 最近の本だとフラーレンやホウ素化合物との関係がよく触れられているが, 実際の測定にはどのような形で役に立つのだろう.

f:id:shironetsu:20180210233514p:plain:w300

*1:『シルトの梯子』の「参考文献」で「負うところ大」と語られているあのジョン・ベイエズ教授. arXivにGreg Egan名義の論文が上がっていることは有名だがそのうちふたつ, スピンネットワークに関するものの共著者でもある. 参考: [gr-qc/0208010] Asymptotics of 10j symbols [gr-qc/0110045] An efficient algorithm for the Riemannian 10j symbols

*2:本来, 単位四元数の群Sp(1)と同型である, と言うべきだが話を単純にするために四元数を行列として導入する.

*3:どうでもいいが"二重"を"2重"と書くべきか迷う. "二重"はさすがに日本語の熟語に属している気がするので漢字で. フォーマルには統一するべきなんでしょうか.

*4:それぞれ一般に通用する記号がついているようだが由来を知らない. ここではアトキンス物理化学に従った.

*5:四元数の有限部分群かつ任意元の-1倍が含まれることから